- 2021-10-26 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师七年级数学上册 第一章二节 同步课时检测卷(附参考答案)
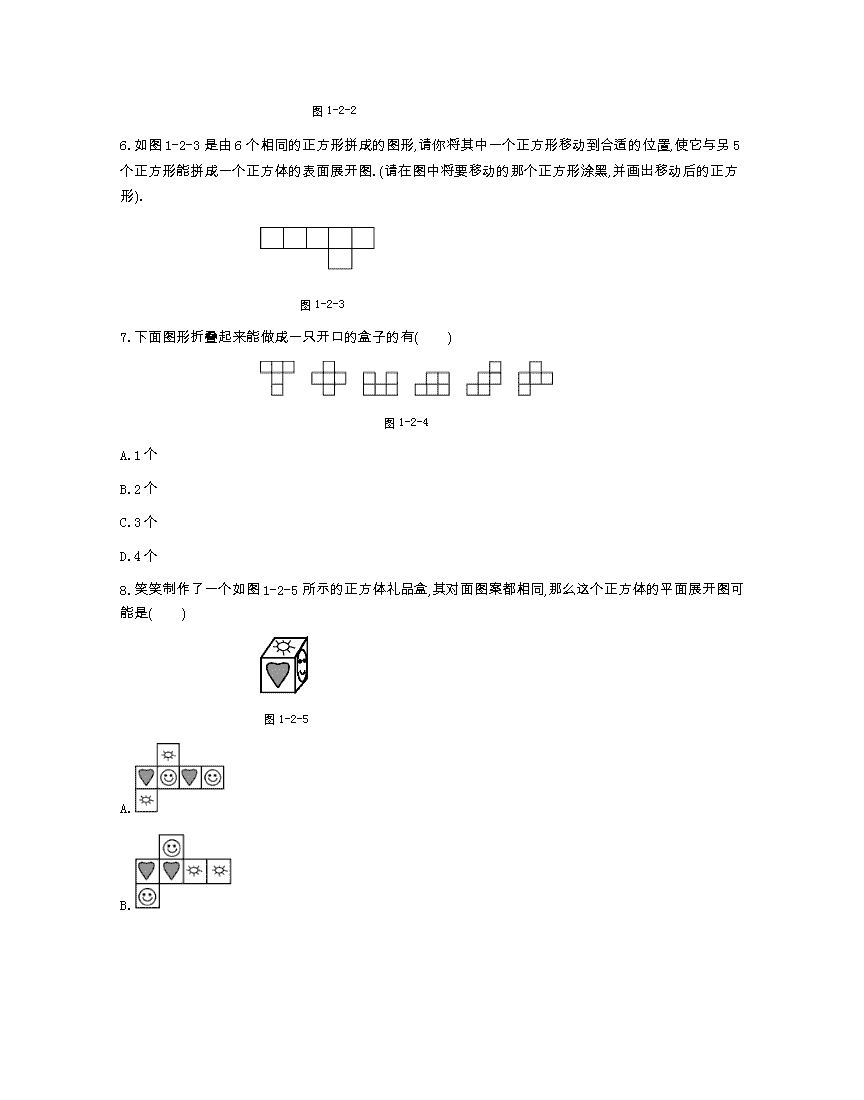
北师七上数学测试题第一章二节 1.正方体有 个面,它们大小 ,且都是 . 2.将一个正方体的表面沿某些棱剪开,展成一个平面图形.不同的剪法,得到的展开图形 ,但展开的图形都是由 个相同的正方形组成. 3.下面图形中,有一个不是正方体的平面展开图,那么不是正方体的平面展开图的图形是( ) A. B. C. D. 4.如图1-2-1所示,图中三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别对应( ) 图1-2-1 A.蓝、绿、黑 B.绿、蓝、黑 C.绿、黑、蓝 D.蓝、黑、绿 5.将如图1-2-2所示的图折叠起来组成一个正方体,数字 所在的平面与数字2所在的平面相对. 图1-2-2 6.如图1-2-3是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形). 图1-2-3 7.下面图形折叠起来能做成一只开口的盒子的有( ) 图1-2-4 A.1个 B.2个 C.3个 D.4个 8.笑笑制作了一个如图1-2-5所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是( ) 图1-2-5 A. B. C. D. 9.如图1-2-6所示,把图形折叠起来会变为( ) 图1-2-6 A. B. C. D. 10.一个正方体的平面展开图如图1-2-7所示,将它折成正方体后“建”字的对面是( ) 图1-2-7 A.和 B.谐 C.社 D.会 11.如图1-2-8,有一个正方体纸巾盒,它的平面展开图是( ) 图1-2-8 A. B. C. D. 12.如图1-2-9是一个正方体纸盒的展开图,其中的六个正方形内分别标有数字“0”“1”“2”“5”和汉字“数”“学”,将其围成一个正方体后,则与“5”相对的是( ) 图1-2-9 A.0 B.2 C.数 D.学 13.如图1-2-10所示,将该图形折叠后可以围成一个正方体,折叠后,回答下列问题。 图1-2-10 (1)点P与哪些点重合?点C与哪些点重合? (2)点A与哪些点重合?点B与哪些点重合? 14.展开图是将立体图形沿某些线剪开,展开成一个 ,同时一个平面图形也可以折叠成一个立体图形. 15.图1-2-11中图形是四棱柱的侧面展开图的是 . ① ② ③ ④ 图1-2-11 16.如图1-2-12所示,若把一个圆锥的侧面沿图示的AB线剪开,则会得到的图形是( ) 图1-2-12 A.三角形 B.圆 C.圆弧 D.扇形 17.将如图1-2-13所示的展开图折叠后形成的立体图形依次是( ) 图1-2-13 A.圆柱、五棱柱、圆锥、三棱柱 B.圆锥、五棱柱、圆柱、三棱锥 C.圆柱、六棱柱、圆锥、三棱锥 D.圆锥、六棱柱、圆柱、三棱柱 18.如图1-2-14所示,能折叠成的长方体是( ) 图1-2-14 A. B. C. D. 19.下面四个图形是多面体的展开图,其中哪一个是四棱锥的展开图( ) A. B. C. D. 20.下面是一些几何体的平面展开图,请写出这些几何体的名称. (1) (2) (3) . (4) (5) (6) . 21.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题. (1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全; (2)若图中的正方形边长为5 cm,长方形的长为8 cm,请计算修正后所折叠而成的长方体的表面积. 图1-2-15 22.在图1-2-16中添加一个小正方形,使该图形折叠后能围成一个四棱柱,不同的添法共有( ) 图1-2-16 A.7种 B.4种 C.3种 D.2种 23.小亮不小心把一个包装盒拆成了如图1-2-17所示的形状,他想按下列要求重新包好这个包装盒(有字母的面向外),请回答。 图1-2-17 (1)若E在前面,C在上面,则F在 面; (2)若C在前面,D在左面,则F在 面; (3)若B在右面,D在后面,则A在 面. 24.如图1-2-18所示,回答下列问题: 图1-2-18 (1)这个棱柱的底面是 形; (2)这个棱柱有 个侧面,侧面的形状是 ; (3)侧面的个数与底面的边数 ;(填“相等”或“不相等”) (4)这个棱柱有 条侧棱,一共有 条棱; (5)如果CC’=3 cm,那么BB’= cm; (6)这个棱柱有 个顶点. 25.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图1-2-19中的①和②.根据你所学的知识,回答下列问题: (1)小明总共剪开了 条棱. (2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全. (3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积. ① ② 图1-2-19 参考答案 1.6 相同 正方形 2.可能不一样 6 3.C 4.B 5.5 6.解:答案如下: 或或等. 7.D 8.A 9.B 10.D 11.B 12.A 13.(1)解:点P与点K,M重合,点C没有重合点. (2)解:点A与点G重合,点B与点D,F重合. 14.平面图形 15.① 16.D 17.C 18.D 19.C 20.(1)正方体 (2)长方体 (3)四棱锥 (4)三棱柱 (5)圆锥 (6)圆柱 21.(1)解:多余一个正方形如图所示: (2)解:表面积=5×5×2+8×5×4 =50+160 =210(cm2). 22.B 23.(1)右 (2)上 (3)上 24.(1)三角 (2)3 平行四边形 (3)相等 (4)3 9 (5)3 (6)6 25.(1)解:小明共剪了8条棱,故答案为:8. (2)解:如图,四种情况. ① ② ③ ④ (3)解:因为长方体纸盒的底面是一个正方形, 所以设最短的棱长高为a cm,则长与宽相等为5a cm, 因为长方体纸盒所有棱长的和是880 cm, 所以4(a+5a+5a)=880,解得a=20 , 所以这个长方体纸盒的体积为:20×100×100=200 000(立方厘米).查看更多