七年级上月考数学试卷(10月)含答案解析

七年级上月考数学试卷(10月)含答案解析

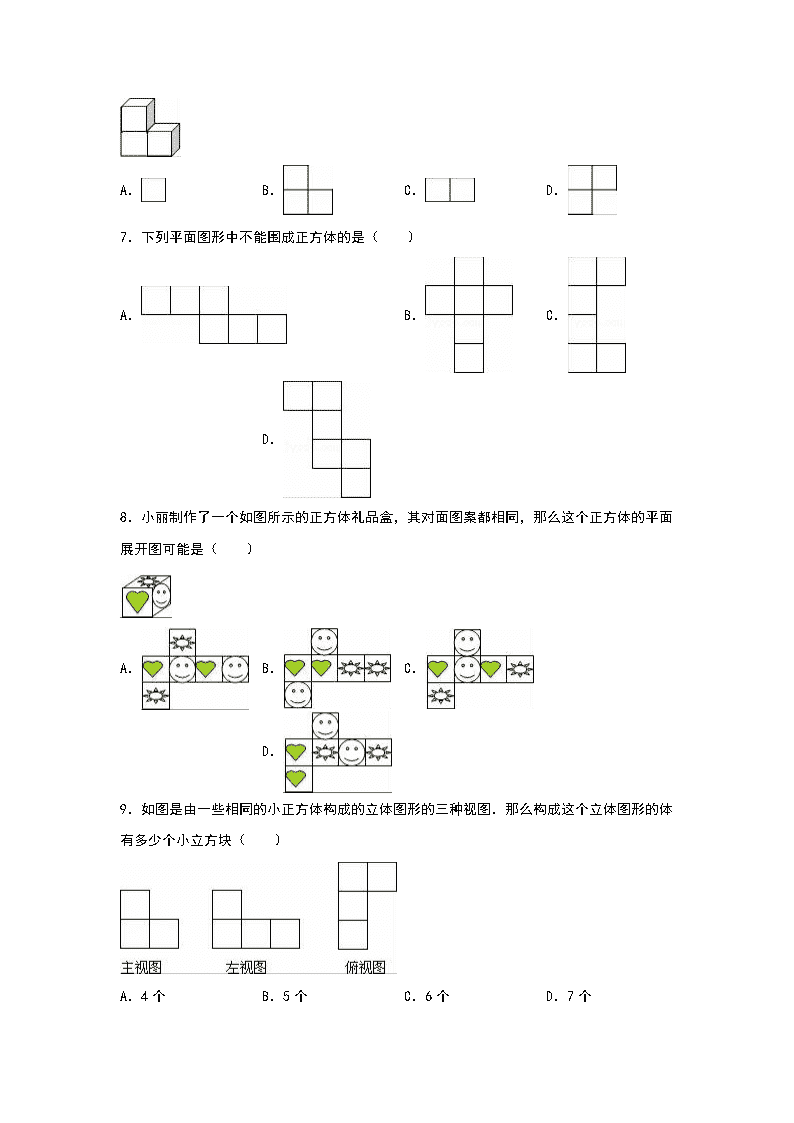
‎2016-2017学年山东省枣庄市七年级（上）月考数学试卷（10月份） ‎ ‎　 ‎ 一、选择题 ‎ ‎1．如图所示几何体的截面是（　　） ‎ ‎ ‎ A．四边形 B．五边形 C．六边形 D．五棱柱 ‎2．用一个平面去截一个正方体，截面的形状不可能是（　　） ‎ A．梯形 B．长方形 C．六边形 D．七边形 ‎3．下列图形经过折叠不能围成棱柱的是（　　） ‎ A． B． C． D．‎ ‎4．如图所示的图形绕虚线旋转一周，所形成的几何体是（　　） ‎ ‎ ‎ A． B． C． D．‎ ‎5．下列所画的数轴中正确的是（　　） ‎ A． B． C． D．‎ ‎6．如图，该物体从上面看是（　　） ‎ ‎ ‎ A． B． C． D．‎ ‎7．下列平面图形中不能围成正方体的是（　　） ‎ A． B． C． D．‎ ‎8．小丽制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（　　） ‎ ‎ ‎ A． B． C． D．‎ ‎9．如图是由一些相同的小正方体构成的立体图形的三种视图．那么构成这个立体图形的体有多少个小立方块（　　） ‎ ‎ ‎ A．4个 B．5个 C．6个 D．7个 ‎10．如图所示，根据有理数a，﹣b，﹣c，在数轴上的位置，比较a，b，c的大小，则有（　　） ‎ ‎ ‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．b＜c＜a ‎11．若x＞0，y＜0，且|x|＜|y|，则x+y一定是（　　） ‎ A．负数 B．正数 C．0 D．无法确定符号 ‎12．下列各式中，正确的是（　　） ‎ A．﹣|﹣16|＞0 B．|0.2|＞|﹣0.2| C．﹣＞﹣ D．|﹣6|＜0‎ ‎　 ‎ 二．填空题：（24分） ‎ ‎13．五棱柱有　　个顶点，有　　条棱，　　个面． ‎ ‎14．在数轴上，离开原点4个单位长度的点表示的数是　　． ‎ ‎15．若a是有理数，则|a|　　0． ‎ ‎16．某地傍晚气温为﹣‎2℃‎，到夜晚下降了‎5℃‎，则夜晚的气温为　　，第二天中午上升了‎10℃‎，则此时温度为　　． ‎ ‎17．一个数a在数轴上对应的点在原点的左边，且|a|=3.5，则a=　　． ‎ ‎18．若要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为6，x=　　，y=　　． ‎ ‎ ‎ ‎　 ‎ 三、解答题 ‎ ‎19．计算题 ‎ ‎（1）（﹣2）+3+1+（﹣3）+2+（﹣4）； ‎ ‎（2）（+26）+（﹣14）+（﹣16）+（+8） ‎ ‎20．画图题： ‎ ‎ （1）如图1是由五块积木搭成，这几块积木都是相同的正方体，请画出这个图形从正面看，左面看，上面看的方向． ‎ ‎（2）如图2是几个正方体所组成的几何体的俯视图，小正方形中的数字表示该位置小正方块的个数．请画出这个几何体的从正面看和上面看到的图形． ‎ ‎ ‎ ‎21．用小立方块搭成的几何体，主视图和俯视图如图，问这样的几何体有多少可能？它最多需要多少小立方块，最少需要多少小立方块，请画出最少和最多时的左视图； ‎ 答：最多　　块； 最少　　块． ‎ 最多时的左视图　　，最少时的左视图　　． ‎ ‎ ‎ ‎22．出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，这天下午他的行车里程（单位：千米）如下： ‎ ‎+15，﹣2，+5，﹣1，+10，﹣3，﹣2，+12，+4，﹣5，+6 ‎ ‎（1）将最后一名乘客送到目的地时，小李距下午出车时的出发点多远？ ‎ ‎（2）若汽车耗油量为‎0.3升/千米，这天下午小李共耗油多少升？ ‎ ‎　 ‎ ‎ ‎ ‎2016-2017学年山东省枣庄市东方国际学校七年级（上）月考数学试卷（10月份） ‎ 参考答案与试题解析 ‎ ‎　 ‎ 一、选择题 ‎ ‎1．如图所示几何体的截面是（　　） ‎ ‎ ‎ A．四边形 B．五边形 C．六边形 D．五棱柱 ‎【考点】截一个几何体． ‎ ‎【分析】根据几何体的形状是五棱柱，进行如图截面即可判断形状． ‎ ‎【解答】解：此几何体是五棱柱， ‎ 故其截面的形状是五边形． ‎ 故选：B． ‎ ‎【点评】本题考查了截一个几何体的应用，目的是培养学生的空间想象能力和动手操作能力． ‎ ‎　 ‎ ‎2．用一个平面去截一个正方体，截面的形状不可能是（　　） ‎ A．梯形 B．长方形 C．六边形 D．七边形 ‎【考点】截一个几何体． ‎ ‎【分析】正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．因此截面的形状可能是：三角形、四边形、五边形、六边形． ‎ ‎【解答】解：用平面去截正方体，得的截面可能为三角形、四边形、五边形、六边形，不可能为七边形． ‎ 故选D． ‎ ‎【点评】本题考查正方体的截面．正方体的截面的四种情况应熟记． ‎ ‎　 ‎ ‎3．下列图形经过折叠不能围成棱柱的是（　　） ‎ A． B． C． D．‎ ‎【考点】展开图折叠成几何体． ‎ ‎【专题】操作型． ‎ ‎【分析】由平面图形的折叠及棱柱的展开图解题． ‎ ‎【解答】解：A可以围成四棱柱，C可以围成五棱柱，D可以围成三棱柱，B选项侧面上多出一个长方形，故不能围成一个三棱柱． ‎ 故选：B． ‎ ‎【点评】熟记常见立体图形的表面展开图的特征是解决此类问题的关键． ‎ ‎　 ‎ ‎4．如图所示的图形绕虚线旋转一周，所形成的几何体是（　　） ‎ ‎ ‎ A． B． C． D．‎ ‎【考点】点、线、面、体． ‎ ‎【分析】上面的直角三角形旋转一周后是一个圆锥，下面的长方形旋转一周后是一个圆柱．所以应是圆锥和圆柱的组合体． ‎ ‎【解答】解：根据以上分析应是圆锥和圆柱的组合体． ‎ 故选：B． ‎ ‎【点评】本题考查的是点、线、面、体知识点，可把较复杂的图象进行分解旋转，然后再组合． ‎ ‎　 ‎ ‎5．下列所画的数轴中正确的是（　　） ‎ A． B．C． D．‎ ‎【考点】数轴． ‎ ‎【分析】运用数轴的三要素判定即可． ‎ ‎【解答】解：根据数轴的三要素判定可得D正确． ‎ 故选：D． ‎ ‎【点评】本题主要考查了数轴，解题的关键是熟记数轴的三要素． ‎ ‎　 ‎ ‎6．如图，该物体从上面看是（　　） ‎ ‎ ‎ A． B． C． D．‎ ‎【考点】简单组合体的三视图． ‎ ‎【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中． ‎ ‎【解答】解：从上面看易得2个正方形． ‎ 故选C． ‎ ‎【点评】本题考查了三视图的知识，俯视图是从物体的上面看得到的视图． ‎ ‎　 ‎ ‎7．下列平面图形中不能围成正方体的是（　　） ‎ A． B． ‎ C． D．‎ ‎【考点】展开图折叠成几何体． ‎ ‎【分析】根据常见的正方体展开图的11种形式以及不能围成正方体的展开图解答即可． ‎ ‎【解答】解：根据常见的不能围成正方体的展开图的形式是“一线不过四，田、凹应弃之”， ‎ 只有C选项不能围成正方体． ‎ 故选C． ‎ ‎【点评】本题考查了正方体展开图，熟记展开图常见的11种形式与不能围成正方体的常见形式“一线不过四，田凹应弃之”是解题的关键． ‎ ‎　 ‎ ‎8．小丽制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（　　） ‎ ‎ ‎ A． B． ‎ C． D．‎ ‎【考点】几何体的展开图． ‎ ‎【分析】本题考查了正方体的展开与折叠．可以动手折叠看看，充分发挥空间想象能力解决也可以． ‎ ‎【解答】解：根据题意及图示只有A经过折叠后符合． ‎ 故选：A． ‎ ‎【点评】本题着重考查学生对立体图形与平面展开图形之间的转换能力，与课程标准中“能以实物的形状想象出几何图形，由几何图形想象出实物的形状”的要求相一致，充分体现了实践操作性原则．要注意空间想象哦，哪一个平面展开图对面图案都相同 ‎ ‎　 ‎ ‎9．如图是由一些相同的小正方体构成的立体图形的三种视图．那么构成这个立体图形的体有多少个小立方块（　　） ‎ ‎ ‎ A．4个 B．5个 C．6个 D．7个 ‎【考点】由三视图判断几何体． ‎ ‎【分析】根据主视图可得这个立体图形共有2层，由俯视图可得第一层小立方块的个数，由主视图和左视图可得第二层小立方块的个数，把所得结果相加即可． ‎ ‎【解答】解：根据图形可得：最底层有4个小立方块， ‎ 第二层有1个小立方块， ‎ 所以构成这个立体图形的小立方块有4+1=5（个）． ‎ 故选B． ‎ ‎【点评】此题考查了由三视图判断几何体，解题的关键是灵活运用三视图，充分发挥空间想象力． ‎ ‎　 ‎ ‎10．如图所示，根据有理数a，﹣b，﹣c，在数轴上的位置，比较a，b，c的大小，则有（　　） ‎ ‎ ‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．b＜c＜a ‎【考点】有理数大小比较；数轴． ‎ ‎【专题】计算题． ‎ ‎【分析】先根据数轴的特点判断出a，﹣b，﹣c的大小及符号，再根据不等式的基本性质便可确定a，b，c的大小． ‎ ‎【解答】解：由数轴上a，﹣b，﹣c的位置可知： ‎ a＜0，﹣c＞0，﹣b＜0，|a|＞|c|， ‎ ‎∴c＜0，a＜c， ‎ ‎∵﹣b＜0， ‎ ‎∴b＞0， ‎ ‎∴a＜c＜b． ‎ 故选B ‎ ‎【点评】本题考查的是有理数的大小比较、数轴上数的特点及不等式的基本性质，由于引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想． ‎ ‎　 ‎ ‎11．若x＞0，y＜0，且|x|＜|y|，则x+y一定是（　　） ‎ A．负数 B．正数 C．0 D．无法确定符号 ‎【考点】绝对值；有理数的加法． ‎ ‎【专题】计算题． ‎ ‎【分析】由题意x＞0，y＜0，说明x在数轴原点的右边，y在左边，然后根据|x|＜|y|，判断谁离原点远些，从而进行求解． ‎ ‎【解答】解：∵x＞0，y＜0， ‎ 又|x|＜|y|， ‎ 说明y值离原点远些，绝对值大， ‎ ‎∴x+y一定是负数． ‎ 故选A． ‎ ‎【点评】此题主要考查绝对值的性质，解题的关键是根据|x|＜|y|，来判断y离原点远些，此题是一道好题． ‎ ‎　 ‎ ‎12．下列各式中，正确的是（　　） ‎ A．﹣|﹣16|＞0 B．|0.2|＞|﹣0.2| C．﹣＞﹣ D．|﹣6|＜0‎ ‎【考点】有理数大小比较． ‎ ‎【专题】推理填空题． ‎ ‎【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可． ‎ ‎【解答】解：∵﹣|﹣16|=﹣16， ‎ ‎∴﹣|﹣16|＜0， ‎ ‎∴选项A不正确； ‎ ‎ ‎ ‎∵|0.2|=0.2，|﹣0.2|=0.2， ‎ ‎∴|0.2|=|﹣0.2|， ‎ ‎∴选项B不正确； ‎ ‎ ‎ ‎∵﹣＞﹣， ‎ ‎∴选项C正确； ‎ ‎ ‎ ‎∵|﹣6|=6， ‎ ‎∴|﹣6|＞0， ‎ ‎∴选项D不正确． ‎ 故选：C． ‎ ‎【点评】此题主要考查了绝对值的含义和求法，以及有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小． ‎ ‎　 ‎ 二．填空题 ‎ ‎13．五棱柱有　10　个顶点，有　15　条棱，　7　个面． ‎ ‎【考点】认识立体图形． ‎ ‎【分析】根据五棱柱的概念和特性可解题． ‎ ‎【解答】解：5棱柱有10个顶点，15条棱，7个面． ‎ 故答案为：10，15，7． ‎ ‎【点评】本题主要考查n棱柱的知识点为：n棱柱有2n个顶点，3n条棱，（n+2）个面． ‎ ‎　 ‎ ‎14．在数轴上，离开原点4个单位长度的点表示的数是　±4　． ‎ ‎【考点】数轴． ‎ ‎【分析】绝对值的意义：数轴上表示这个数的点到原点的距离就是这个数的绝对值． ‎ ‎【解答】解：根据绝对值的意义，得离开原点4个单位长度的点表示的数，即绝对值是4的数是±4． ‎ ‎【点评】理解绝对值的意义． ‎ ‎　 ‎ ‎15．若a是有理数，则|a|　≥　0． ‎ ‎【考点】绝对值． ‎ ‎【分析】利用绝对值的性质即可解答． ‎ ‎【解答】解：当a＞0时，|a|=a＞0； ‎ 当a＜0时，|a|=﹣a＞0，； ‎ 当a=0时，|a|=a=0， ‎ 综上所述， ‎ ‎|a|≥0， ‎ 故答案为：≥． ‎ ‎【点评】本题主要考查了绝对值的性质，理解绝对值的性质是解答此题的关键． ‎ ‎　 ‎ ‎16．某地傍晚气温为﹣‎2℃‎，到夜晚下降了‎5℃‎，则夜晚的气温为　﹣‎7℃‎　，第二天中午上升了‎10℃‎，则此时温度为　+‎3℃‎　． ‎ ‎【考点】有理数的减法；有理数的加法． ‎ ‎【专题】计算题． ‎ ‎【分析】气温下降用减法，上升用加法，列式计算即可． ‎ ‎【解答】解：夜晚的气温=﹣2﹣5=﹣（2+5）=﹣‎7℃‎， ‎ 第二天中午的气温=﹣7+10=10﹣7=‎3℃‎． ‎ ‎【点评】本题主要考查有理数的加减法，减法法则：减去一个数等于加上这个数的相反数．这是需要熟记的内容． ‎ ‎　 ‎ ‎17．一个数a在数轴上对应的点在原点的左边，且|a|=3.5，则a=　﹣3.5　． ‎ ‎【考点】绝对值；数轴． ‎ ‎【分析】数a在数轴上的对应点在原点的左边，即这个数是负数，再根据绝对值即可确定a的值． ‎ ‎【解答】解：∵|a|=3.5， ‎ ‎∴a=±3.5， ‎ ‎∵数a在数轴上对应的点在原点的左边， ‎ ‎∴a=﹣3.5． ‎ 故答案为：﹣3.5． ‎ ‎【点评】本题考查了数轴和绝对值．关键是掌握数轴上，原点左边的数是负数，原点右边的数是正数． ‎ ‎　 ‎ ‎18．若要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为6，x=　5　，y=　3　． ‎ ‎ ‎ ‎【考点】专题：正方体相对两个面上的文字． ‎ ‎【专题】数形结合． ‎ ‎【分析】利用正方体及其表面展开图的特点解题． ‎ ‎【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“‎1”‎与面“x”相对，面“‎3”‎与面“y”相对． ‎ 因为相对面上两个数之和为6，所以，x=5，y=3． ‎ 故答案为：5，3． ‎ ‎【点评】注意正方体的空间图形，从相对面入手，分析及解答问题． ‎ ‎　 ‎ 三、解答题 ‎ ‎19．计算题 ‎ ‎（1）（﹣2）+3+1+（﹣3）+2+（﹣4）； ‎ ‎（2）（+26）+（﹣14）+（﹣16）+（+8） ‎ ‎【考点】有理数的加法． ‎ ‎【分析】（1）根据有理数的加减混合运算进行计算即可； ‎ ‎（2）根据有理数的加减混合运算进行计算即可． ‎ ‎【解答】解：（1）原式=﹣2+3+1﹣3+2﹣4 ‎ ‎=﹣3； ‎ ‎（2）原式=26﹣14﹣16+8 ‎ ‎=34﹣30 ‎ ‎=4． ‎ ‎【点评】本题考查了有理数的加减混合运算，掌握运算法则是解题的关键． ‎ ‎　 ‎ ‎20．画图题： ‎ ‎ （1）如图1是由五块积木搭成，这几块积木都是相同的正方体，请画出这个图形从正面看，左面看，上面看的方向． ‎ ‎（2）如图2是几个正方体所组成的几何体的俯视图，小正方形中的数字表示该位置小正方块的个数．请画出这个几何体的从正面看和上面看到的图形． ‎ ‎ ‎ ‎【考点】作图-三视图；由三视图判断几何体． ‎ ‎【分析】（1）从正面看从左往右2列正方形的个数依次为3，1；从左面看从左往右2列正方形的个数依次为3，1；从上面看从左往右2列正方形的个数依次为2，1；画出从正面，左面，上面看，得到的图形即可． ‎ ‎（2）由已知条件可知，主视图有3列，每列小正方数形数目分别为3，2，4；左视图有3列，每列小正方形数目分别为2，3，4．据此可画出图形． ‎ ‎【解答】解：（1）如图所示： ‎ ‎ ‎ ‎（2）如图所示： ‎ ‎ ‎ ‎【点评】本题考查了作图﹣﹣三视图、由三视图判断几何体，本题画几何体的三视图时应注意小正方形的数目及位置． ‎ ‎　 ‎ ‎21．用小立方块搭成的几何体，主视图和俯视图如图，问这样的几何体有多少可能？它最多需要多少小立方块，最少需要多少小立方块，请画出最少和最多时的左视图； ‎ 答：最多　8　块； 最少　7　块． ‎ 最多时的左视图　　，最少时的左视图　　． ‎ ‎ ‎ ‎【考点】由三视图判断几何体． ‎ ‎【分析】易得这个几何体共有3层，由俯视图可得第一层正方体的个数为4，由主视图可得第二层最少为2块，最多的正方体的个数为3块，第三层只有一块，相加即可． ‎ ‎【解答】解：有两种可能； ‎ 有主视图可得：这个几何体共有3层， ‎ 由俯视图可得：第一层正方体的个数为4，由主视图可得第二层最少为2块，最多的正方体的个数为3块， ‎ 第三层只有一块， ‎ 故：最多为3+4+1=8个小立方块，最少为个2+4+1=7小立方块． ‎ 最多时的左视图是： ‎ ‎ ‎ 最少时的左视图为： ‎ ‎ ‎ ‎【点评】此题主要考查了由三视图判断几何体，关键是掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就很容易得到答案． ‎ ‎　 ‎ ‎22．出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，这天下午他的行车里程（单位：千米）如下： ‎ ‎+15，﹣2，+5，﹣1，+10，﹣3，﹣2，+12，+4，﹣5，+6 ‎ ‎（1）将最后一名乘客送到目的地时，小李距下午出车时的出发点多远？ ‎ ‎（2）若汽车耗油量为‎0.3升/千米，这天下午小李共耗油多少升？ ‎ ‎【考点】正数和负数． ‎ ‎【分析】（1）根据有理数的加法，可得答案； ‎ ‎（2）根据单位耗油量乘以行驶路程，可得答案． ‎ ‎【解答】解：（1）+15+（﹣2）+5+（﹣1）+10+（﹣3）+（﹣2）+12+4+（﹣5）+6 ‎ ‎=（15+5+10+12+4+6）+[+（﹣1）+（﹣3）+（﹣2）+（﹣5）] ‎ ‎52+（﹣13）=‎39km， ‎ 将最后一名乘客送到目的地时，小李距下午出车时的出发点‎39km； ‎ ‎（2）（2+|﹣13|）×0.3=65×0.3=‎19.5升， ‎ 这天下午小李共耗油‎19.5升． ‎ ‎【点评】本题考查了正数和负数，利用单位耗油量乘以行驶路程是解题关键． ‎ ‎　 ‎