- 2021-10-25 发布 |
- 37.5 KB |
- 5页
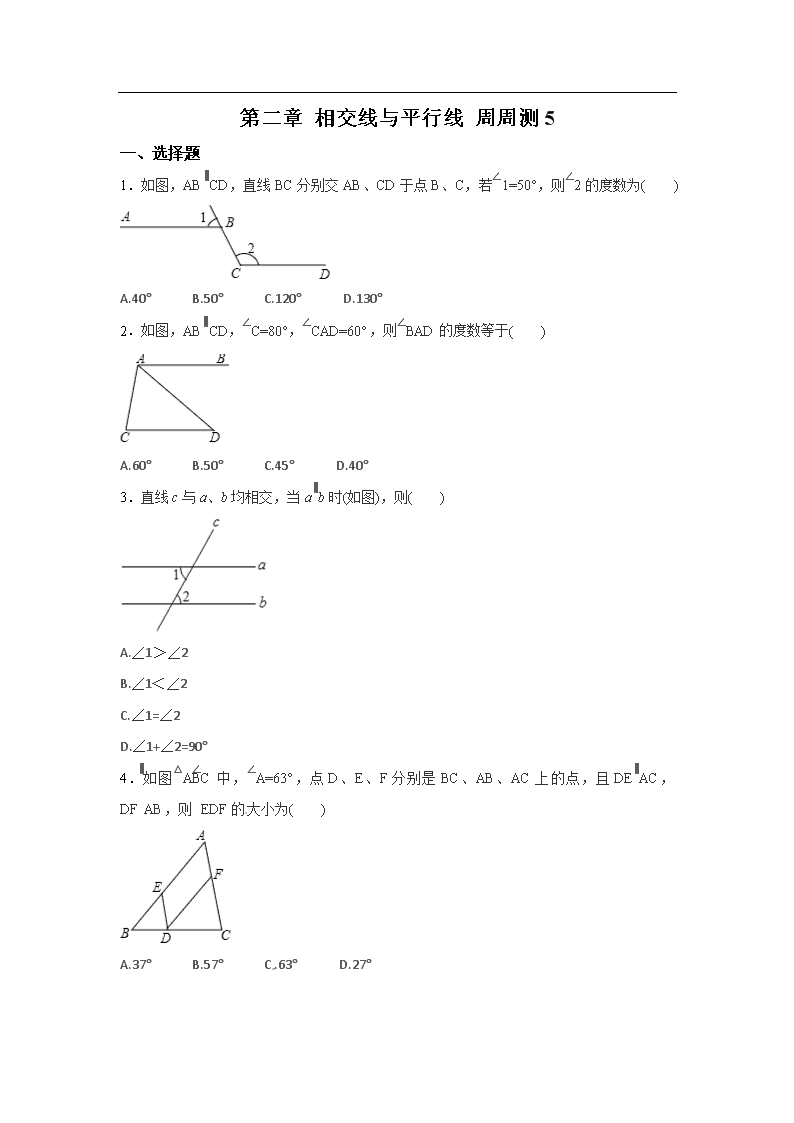

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学第二章 相交线与平行线 周周测5(2-3~2-4) 北师大版
第二章 相交线与平行线 周周测5 一、选择题 1.如图,AB∥CD,直线BC分别交AB、CD于点B、C,若∠1=50°,则∠2的度数为( ) A.40° B.50° C.120° D.130° 2.如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) A.60° B.50° C.45° D.40° 3.直线c与a、b均相交,当a∥b时(如图),则( ) A.∠1>∠2 B.∠1<∠2 C.∠1=∠2 D.∠1+∠2=90° 4.如图△ABC中,∠A=63°,点D、E、F分别是BC、AB、AC上的点,且DE∥AC,DF∥AB,则∠EDF的大小为( ) A.37° B.57° C.63° D.27° 5.一轮船航行到B处测得小岛A的方向为北偏西30°,那么从A处观测B处的方向为( ) A.南偏东30° B.东偏北30° C.南偏东60° D.东偏北60°[来源:Z§xx§k.Com] 6.如图,已知a∥b,∠1=50°,则∠2=( ) [来源:学科网] A.40° B.50° C.120° D.130° 7.下列叙述中,正确的是( ) A.以点O为圆心,以任意长为半径画弧,交线段OA于点B B.以∠AOB的边OB为一边作∠BOC C.以点O为圆心画弧,交射线OA于点B D.在线段AB的延长线上截取线段BC=AB 8.下列属于尺规作图的是( ) A.用量角器画∠AOB的平分线OP B.利用两块三角板画15°的角 C.用刻度尺测量后画线段AB=10cm D.在射线OP上截取OA=AB=BC=a 二、填空题[来源:学*科*网Z*X*X*K] 9.如图,已知直线a∥b,∠1=85°,则∠2=_____. 10.探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=_____. 11.如图,一束光线以入射角为50°的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成30°的角,则CD与地面AB 所成的角∠CDA 的度数是_____. AB 12.两个角的两边分别平行,且其中一个角比另一个角的2倍少15°,则这两个角为_____. 13.下列语句表示的图形是(只填序号) ①过点O的三条直线与另条一直线分别相交于点B、C、D三点: . ②以直线AB上一点O为顶点,在直线AB的同侧画∠AOC和∠BOD: . ③过O点的一条直线和以O为端点两条射线与另一条直线分别相交于点B、C、D三点: . 14.下列语句是有关几何作图的叙述. ①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有 .(填序号即可) 三、解答题[来源:Zxxk.Com] 15. 如图,AB∥CD,直线EF分别交AB,CD于点E,F,点G是AB上一点,GO⊥EF于点O,∠1=60°,求∠2的度数. 16.解放战争时期,某天江南某游击队从村庄A处出发向正东方向行进,此时有一支残匪在游击队的东北方向B处,残匪沿北偏东60°方向向C村进发,游击队步行到A′(A′在B的正南方向)处时,突然接到上级命令,决定改变行进方向,沿北偏东30°方向赶往C村,问:游击队的进发方向A′C与残匪的行进方向BC至少成多大角度时,才能保证C村村民不受伤害?[来源:学#科#网] 17.如图,AB∥CD,AD∥BC,若∠A=73°,求∠B、∠C、∠D的度数. 18.如图,已知在△ABC中,AD平分∠EAC且AD∥BC,那么∠B=∠C吗?请说明理由. 19.如图,AD平分∠BAC,DE∥AC,DF∥AB,图中∠1与∠2有什么关系?为什么? 第二章 相交线与平行线 周周测5参考答案与解析 1. D 2. D 3. C 4. C 5. A 6. D 7. D 8. D 9. 85 10. 95 11. 80 12. 15 ,15 或65 ,115 13.(3) (2) (1) 14. ③⑤ 15. 解析:∵OG⊥EF,(已知) ∴∠EOG=90°,(垂直的定义) ∴∠2+∠GEO=90°.(三角形内角和定理) 又∵AB∥CD,(已知) ∴∠GEF=∠1=60°.(两直线平行,内错角相等) ∴∠2=30°.(等式的性质) . 16.解:如图. ∵BA′∥CM, ∴∠A′CM=∠BA′C=30°. ∵CN∥BE, ∴∠BCN=∠CBE=30°, ∴∠BCA′=90°-30°-30°=30°, 故A′C与BC的夹角至少为30°时,才能保证C村村民不受伤害 . 17.解:∵AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形, ∴∠C=∠A=73°, ∴∠B=∠D=180°-∠A=107°. 18.解:∠B=∠C.理由如下: ∵AD∥BC, ∴∠EAD=∠B,∠DAC=∠C. ∵AD平分∠EAC, ∴∠EAD=∠DAC. ∴∠B=∠C. 19.解:∠1=∠2. 理由如下: ∵DE∥AC,DF∥AB, ∴∠1=∠DAF,∠2=∠DAE, 又∵AD平分∠BAC, ∴∠DAF=∠DAE, ∴∠1=∠2. 查看更多