2019七年级数学上册 第5章 相交线与平行线 5平行线的性质

2019七年级数学上册 第5章 相交线与平行线 5平行线的性质

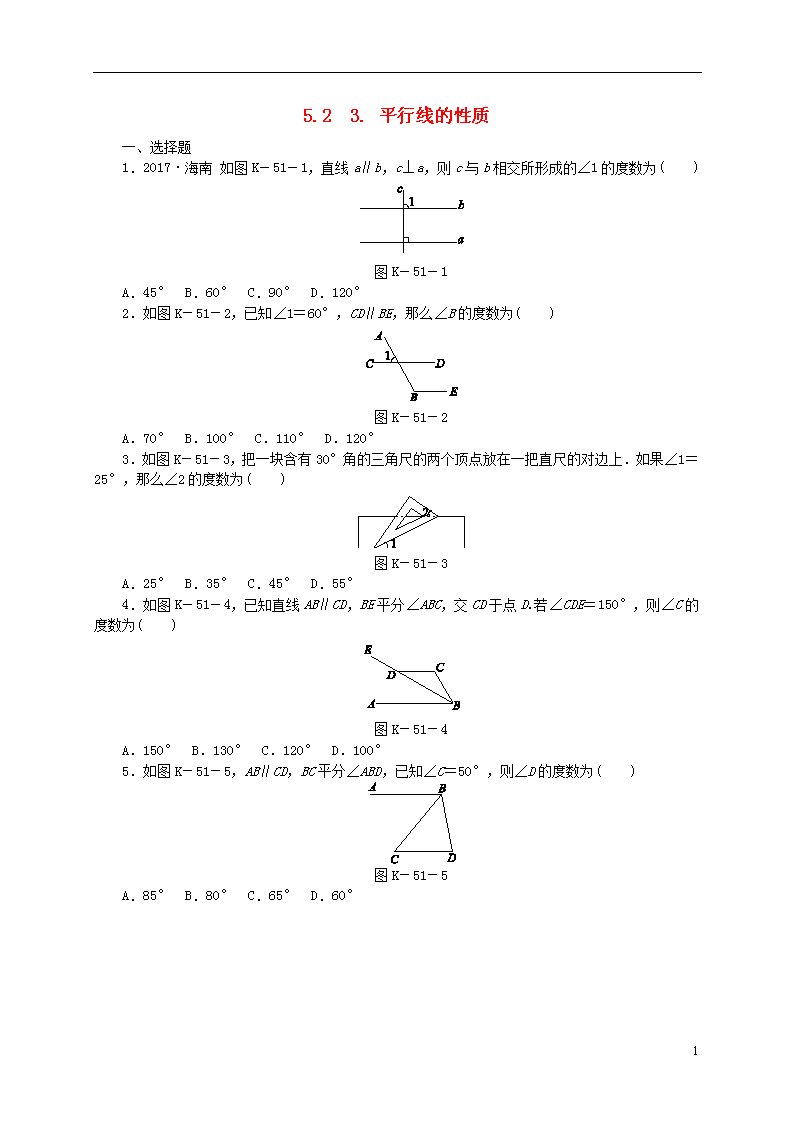
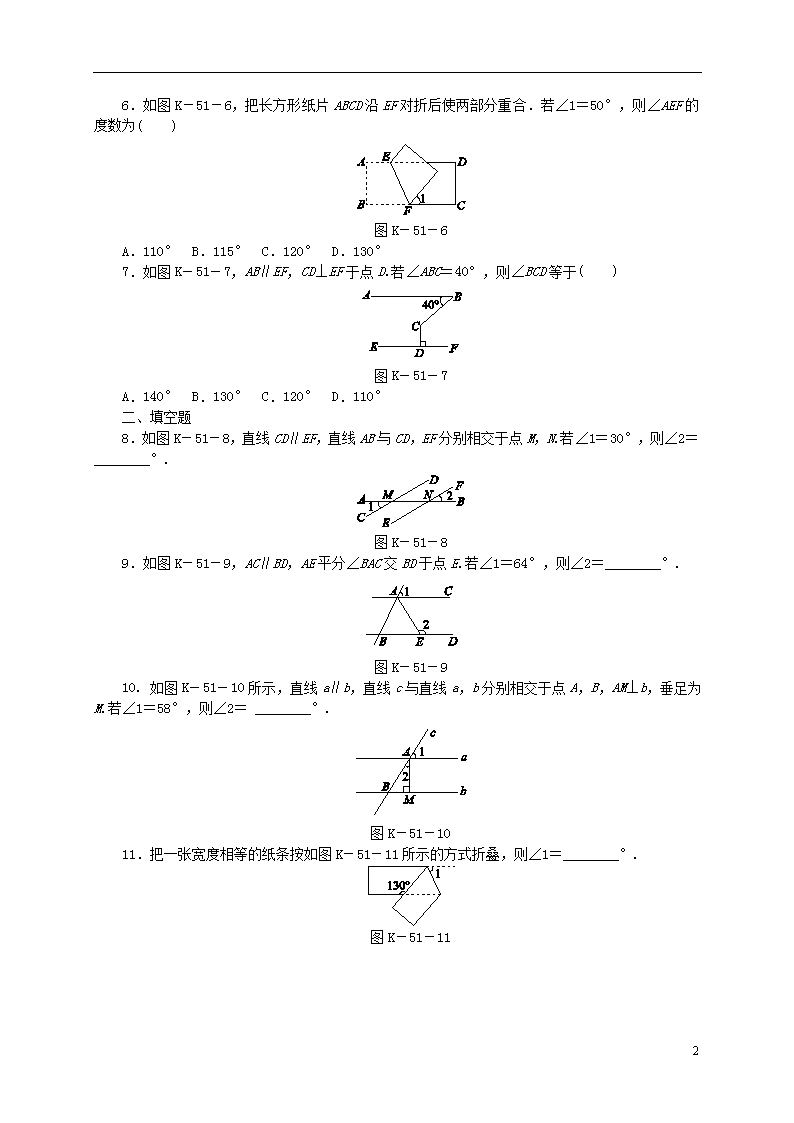
‎5.2　3. 平行线的性质 一、选择题 ‎1．2017·海南 如图K－51－1，直线a∥b，c⊥a，则c与b相交所形成的∠1的度数为(　　)‎ ‎ ‎ 图K－51－1‎ A．45° B．60° C．90° D．120°‎ ‎2．如图K－51－2，已知∠1＝60°，CD∥BE，那么∠B的度数为(　　)‎ 图K－51－2‎ A．70° B．100° C．110° D．120°‎ ‎3．如图K－51－3，把一块含有30°角的三角尺的两个顶点放在一把直尺的对边上．如果∠1＝25°，那么∠2的度数为(　　)‎ 图K－51－3‎ A．25° B．35° C．45° D．55°‎ ‎4．如图K－51－4，已知直线AB∥CD，BE平分∠ABC，交CD于点D.若∠CDE＝150°，则∠C的度数为(　　)‎ 图K－51－4‎ A．150° B．130° C．120° D．100°‎ ‎5．如图K－51－5，AB∥CD，BC平分∠ABD，已知∠C＝50°，则∠D的度数为(　　)‎ 图K－51－5‎ A．85° B．80° C．65° D．60°‎ ‎　　　‎ 6‎ ‎6．如图K－51－6，把长方形纸片ABCD沿EF对折后使两部分重合．若∠1＝50°，则∠AEF的度数为(　　)‎ 图K－51－6‎ A．110° B．115° C．120° D．130°‎ ‎7．如图K－51－7，AB∥EF，CD⊥EF于点D.若∠ABC＝40°，则∠BCD等于(　　)‎ 图K－51－7‎ A．140° B．130° C．120° D．110°　　‎ 二、填空题 ‎8．如图K－51－8，直线CD∥EF，直线AB与CD，EF分别相交于点M，N.若∠1＝30°，则∠2＝________°.‎ 图K－51－8‎ ‎9．如图K－51－9，AC∥BD，AE平分∠BAC交BD于点E.若∠1＝64°，则∠2＝________°.‎ 图K－51－9‎ ‎10. 如图K－51－10所示，直线a∥b，直线c与直线a，b分别相交于点A，B，AM⊥b，垂足为M.若∠1＝58°，则∠2＝ ________°.‎ 图K－51－10‎ ‎11．把一张宽度相等的纸条按如图K－51－11所示的方式折叠，则∠1＝________°.‎ 图K－51－11‎ ‎　　　‎ 6‎ ‎12．如图K－51－12，在△ABC中，∠C＝90°.若BD∥AE，∠DBC＝22°，则∠CAE的度数是________．‎ 图K－51－12‎ 三、解答题 ‎13．如图K－51－13，已知∠1＝∠2，∠A＝∠F，试说明：∠C＝∠D.请补充说明过程，并在括号内填上相应理由．‎ 图K－51－13‎ 解：∵∠1＝∠2(已知)，∠1＝∠3(____________)，‎ ‎∴∠2＝∠3(__________)，‎ ‎∴BD∥________(____________________________)，‎ ‎∴∠FEM＝∠D(________________________)．‎ ‎∵∠A＝∠F(已知)，‎ ‎∴AC∥________(______________________)，‎ ‎∴∠C＝∠FEM(___________________________________)．‎ 又∵∠FEM＝∠D(已证)，‎ ‎∴∠C＝∠D(等量代换)．‎ ‎14．如图K－51－14，直线AB，CD分别与直线AC相交于点A，C，与直线BD相交于点B，D.若∠1＝∠2，∠3＝75°，求∠4的度数．‎ 图K－51－14‎ ‎15．如图K－51－15，已知AB∥CE，∠A＝∠E.试说明：∠CGD＝∠FHB.‎ 图K－51－15‎ 6‎ ‎16．如图K－51－16所示，在△ABC中，∠1∶∠2∶∠3＝2∶3∶4，DE∥AB.若∠C＝40°，求∠A和∠B的度数．‎ 图K－51－16‎ ‎17．在三角形中，每两边所组成的角叫三角形的内角，如图K－51－17，在三角形ABC中，∠A，∠B和∠C是它的三个内角．在学习了平行线的性质以后，我们可以用几何推理的方法说明“三角形的内角和等于180°”．‎ 已知三角形ABC，试说明∠A＋∠B＋∠C＝180°.‎ 图K－51－17‎ 6‎ ‎1．C　‎ ‎2．D ‎3．B　.‎ ‎4．C　.‎ ‎5．B　.‎ ‎6．B ‎7． B　.‎ ‎8．30　‎ ‎9．122　.‎ ‎10．32‎ ‎11．65　12．68°‎ ‎13．对顶角相等　等量代换　CE　同位角相等，两直线平行　两直线平行，同位角相等　DF　内错角相等，两直线平行　两直线平行，内错角相等 ‎14．解：因为∠1＝∠2，所以AB∥CD(同位角相等，两直线平行)，所以∠3＝∠4(两直线平行，内错角相等)，所以∠4＝75°.‎ ‎15．解：∵AB∥CE，‎ ‎∴∠E＝∠BFH.‎ ‎∵∠A＝∠E，‎ ‎∴∠A＝∠BFH，‎ ‎∴AD∥EF，‎ ‎∴∠CGD＝∠EHC.‎ 又∵∠FHB＝∠EHC，‎ ‎∴∠CGD＝∠FHB.‎ ‎16．解：因为∠1∶∠2∶∠3＝2∶3∶4，‎ 且∠1＋∠2＋∠3＝180°，‎ 所以∠1＝180°×＝40°，∠2＝180°×＝60°，∠3＝180°×＝80°.‎ 又因为∠C＝40°，‎ 所以∠1＝∠C，‎ 所以EF∥BC(同位角相等，两直线平行)，‎ 所以∠2＝∠EDC(两直线平行，内错角相等)，‎ 所以∠EDC＝60°.‎ 因为DE∥AB，所以∠A＝∠3＝80°，‎ ‎∠B＝∠EDC＝60°(两直线平行，同位角相等)．‎ ‎17．作BC的延长线CD，过点C作CE∥AB，如图所示．‎ 因为CE∥AB(已作)，所以∠A＝∠ACE(两直线平行，内错角相等)，∠B＝∠ECD(两直线平行，同位角相等)．又因为∠ACB＋∠ACE＋∠ECD＝180°(平角的定义)，所以∠A＋∠B＋∠ACB＝180°. ‎ 6‎ 6‎