七年级数学下册第6章一元一次方程6-2解一元一次方程1等式的性质与方程的简单变形课件1

七年级数学下册第6章一元一次方程6-2解一元一次方程1等式的性质与方程的简单变形课件1

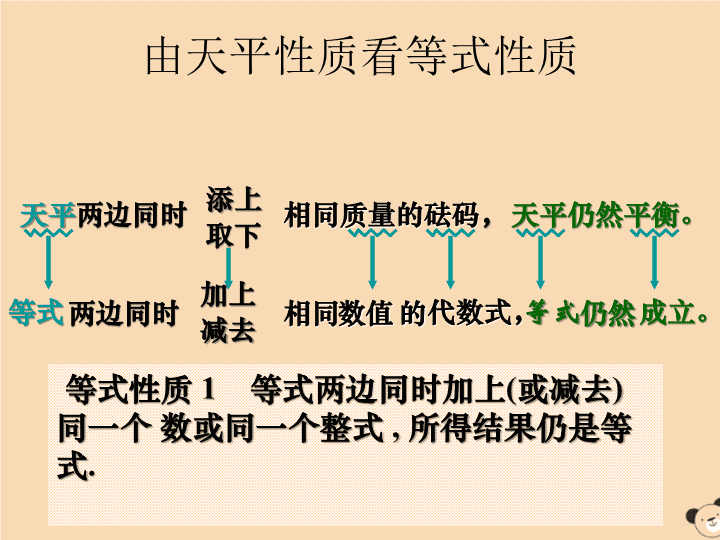
方程的简单变形6.2解一元一次方程第一课时 天平与等式把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等号成立就可看作是天平保持两边平衡。等式左边等式右边等号 由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码，两边同时相同的仍然等式加上减去数值代数式，等式成立。等式性质1等式两边同时加上(或减去)同一个数或同一个整式,所得结果仍是等式. 等式的性质如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一)，那么天平还保持两边平衡吗?于是,你又能得出等式的什么性质?试用准确、简明的语言叙述之.等式的性质2等式两边都乘以同一个数(或除以）同一个数（除数不能为0）,所得结果仍是等式. 用等式的性质解方程例1解下列方程：(1)x－5=7;(2)4x=3x－4；这几小题中的方程的变形有什么共同的特点？ 解:(1)由x－5=7两边都加上5，得x＝7+5即，x＝12(2)由4x=3x－4;两边都减去3x，得4x-3x＝－4即，x＝－4 归纳像这样，将方程两边都加上(或减去)同一个数或同一个整式，就相当于把方程中的某些项改变符号后，从方程的一边移到另一边，这样的变形叫做移项。注意：“移项”是指将方程的某些项从等号的左边移到右边或从右边移到左边，移项时要先变号。 用等式的性质解方程例2解下列方程：(1)-5x=2;(2) 归纳这两个方程的解法，都依据了等式的性质2，将方程的两边都除以未知数的系数。像这样的变形通常称作“将未知数的系数化为1”。 解下列方程：（1）10x－3＝9（2）6x－7＝4x－5 本节课你的收获是什么？这节课我们利用天平原理得出了等式的两个性质，并初步学习了用等式的两个性质解简单方程。所谓“方程解完了”，意味着经过对原方程的一系列变形(两边同加减、乘除)，最终把方程化为最简的形式：x=c即方程左边只一个未知数项、右边只一个常数项，且未知数项的系数是1. 再见