七年级数学下册第三章变量之间的关系2用关系式表示的变量间关系课件（新版）北师大版

七年级数学下册第三章变量之间的关系2用关系式表示的变量间关系课件（新版）北师大版

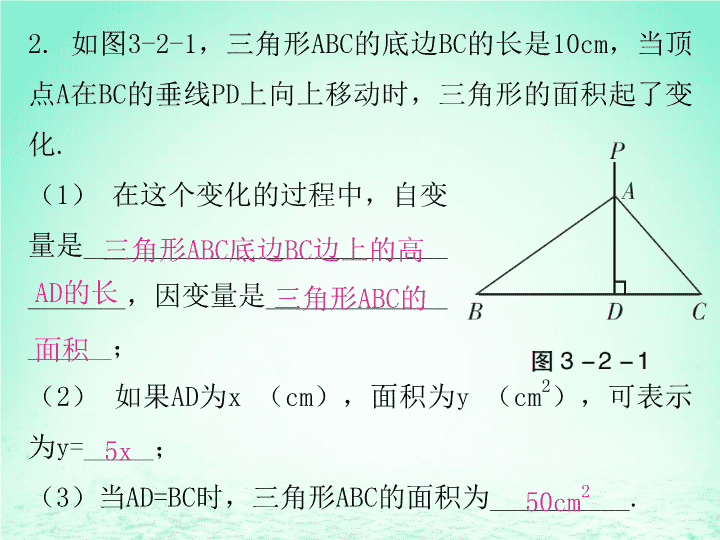
2用关系式表示的变量间关系第三章变量之间的关系 课前预习1.变量x与y之间的关系是y=x2-3，当自变量x=2时，因变量y的值是（）A.-2B.-1C.1D.2B 2.如图3-2-1，三角形ABC的底边BC的长是10cm，当顶点A在BC的垂线PD上向上移动时，三角形的面积起了变化.（1）在这个变化的过程中，自变量是_________________________________，因变量是___________________；（2）如果AD为x（cm），面积为y（cm2），可表示为y=_____；（3）当AD=BC时，三角形ABC的面积为__________.AD的长三角形ABC底边BC边上的高三角形ABC的面积5x50cm2 3.设地面气温为20℃，如果每升高1km，气温下降6℃，在这个变化过程中，自变量是__________，因变量是__________，如果高度用h（千米）表示，气温用t（℃）表示，那么t随h的变化而变化的关系式为________________.4.一列火车以60km/h的速度行驶，它驶过的路程s（km）和所用时间t（h）用关系式可表示为_______.高度气温t=-6h+20s=60t 课堂讲练新知变量关系式典型例题【例1】如图3-2-2，梯形的上底为x，下底为8，高为4.（1）求梯形的面积y与x的关系；（2）用表格表示当x从5到10时（每次增加1），y的相应值；（3）当x每增加1时，y如何变化？（4）当y=50时，x为；（5）当x=0时，y等于什么？此时它表示的是什么？ 解:（1）梯形的面积与上底长之间的关系是y=2x+16.（2）当x从5到10时（每次增加1），y的相应值为y263032x5678910362834（3）当x每增加1时，相应的y值依次增加2.（4）把y=50代入y=2x+16中，得到x=17.（5）当x=0时，y等于16.此时所表示的是底边为8，高为4的三角形的面积. 【例2】一辆汽车油箱内有油56L，从某地出发，每行驶1km，耗油0.08L，如果设油箱内剩油量为y（L），行驶路程为x（km），则y随x的变化而变化.（1）在上述变化过程中，自变量是__________；因变量是__________；（2）用表格表示汽车从出发地行驶100km,200km,300km,400km时的剩油量.请将表格补充完整：行驶路程x/km油箱内剩油量y/L1002003004004024 （3）试写出y与x的关系式：__________；（4）这辆汽车行驶350km时剩油多少升？汽车剩油8L时，行驶了多少千米？解：（1）汽车行驶路程油箱内剩油量（2）56-0.08×100=48，56-0.08×300=32.行驶路程x/km油箱内剩油量y/L10020030040040244832 （3）y=56-0.08x.（4）当x=350时，y=56-0.08×350=28，所以汽车行驶350km时剩油28L.当y=8时，56-0.08x=8，解得x=600.所以汽车行驶600km时剩油8L. 模拟演练1.用一根长是20cm的细绳围成一个长方形（如图3-2-3），这个长方形的一边的长为xcm，它的面积为ycm2.（1）写出y与x之间的关系式，在这个关系式中，哪个是自变量？它的取值应在什么范围内？（2）用表格表示当x从1变到9时（每次增加1），y的相应值；（3）从上面的表格中，你能看出什么规律？（4）估计一下，当围成的长方形的面积是22cm2时，x的值应介于哪两个相邻整数之间？ 解：（1）y=·x=（10-x）·x，x是自变量，它的值应在0~10之间（不包括0和10）.20-2x2（2）当x从1到9时（每次增加1），y的相应值为y92124x12341625241695678921 （3）可以看出：①当x逐渐增大时，y的值先由小变大，后又由大变小；②y的值在由小变大的过程中，变大的速度越来越慢，反过来y的值在由大变小的过程中，变小的速度越来越快；③当x取距5等距离的两数时，得到的两个y值相等.（4）根据表格，当y=22时，x应介于3和4之间或者6和7之间. 2.将长为40cm，宽为15cm的长方形白纸，按图3-2-4所示的方法粘合起来，粘合部分宽为5cm.（1）根据图，将下表格补充完整.白纸张数/张纸条长度/cm1234401105…145 （2）设x张白纸粘合后的总长度为ycm，则y与x之间的关系式是什么？（3）你认为白纸粘合起来总长度可能为2017cm吗？为什么？解：（1）75180（2）y=40+35（x-1）=35x+5.（3）不能.理由如下：根据题意，得2017=35x+5，解得x≈57.5.因为x为整数，所以不能. 课后作业新知变量关系式1.长方形的周长为24cm，其中一边长为x（x＞0）cm，面积为ycm2，则y与x的关系式为（　）A.y=x2B.y=（24-x）xC.y=（12-x）2D.y=（12-x）xD 2.小张为自己已经用光话费的手机充值100元，他购买的服务是：20元/月包接听，主叫0.2元/min.这个月内，他手机所剩话费y（元）与主叫时间t（min）之间的关系式是（　）A.y=100-0.2tB.y=80-0.2tC.y=100+0.2tD.y=80+0.2tB 3.一根弹簧原长12cm，它所挂的重量不超过10kg，并且挂重1kg就伸长1.5cm，写出挂重后弹簧长度y（cm）与挂重x（kg）之间的关系式是（　）A.y=1.5（x+12）（0≤x≤10）B.y=1.5x+12（0≤x≤10）C.y=1.5x+12（x≥0）D.y=1.5（x-12）（0≤x≤10）B 4.如图3-2-5所示，在三角形ABC中，已知BC=16，高AD=10，动点Q由C点沿CB向B移动（不与点B重合）.设CQ长为x，三角形ACQ的面积为S，则S与x之间的关系式为（　）A.S=80-5xB.S=5xC.S=10xD.S=5x+80B 5.从A地向B地打长途电话，按时收费，3min内收费2.4元，以后每超过1min加收1元，若通话t（t≥3）min，则需付电话费y（元）与t（min）之间的关系式是（　）A.y=t-0.5B.y=t-0.6C.y=3.4t-7.8D.y=3.4t-8B 6.声音在空气中传播的速度与气温的关系如下表，根据表格分析下列说法错误的是（　）A.在这个变化过程中，气温是自变量，声速是因变量B.声速随气温的升高而增大C.声速v与气温T的关系式为v=T+330D.气温每升高10℃，声速增加6m/sC气温T/℃声速v/（m·s-1）-20-100103183302030336324342348 7.在一边长为2的正方形中挖一个边长为x（0＜x＜2）的小正方形，如果设剩余部分的面积为y，那么y关于x的关系式是______________________.8.某商店进了一批货，每件3元，出售时每件加价0.5元，如售出x件应收入货款y元，那么y（元）与x（件）的关系式是__________.9.一个矩形的面积为20cm2，相邻两条边长分别为xcm和ycm，那么变量y与变量x的关系式为______________________.y=-x2+4（0＜x＜2）y=3.5xy=（0＜x＜20） 能力提升10.某剧院的观众席的座位为扇形，且按下表方式设置：（1）按照上表所示的规律，当x每增加1时，y如何变化？（2）写出座位数y与排数x之间的关系式；（3）按照上表所示的规律，某一排可能有90个座位吗？说说你的理由.排数（x）座位数（y）12345053…5956… 解：（1）由图表中数据，得当x每增加1时，y增加3.（2）由题意,得y=50+3（x-1）=3x+47.（3）某一排不可能有90个座位，理由：由题意，得y=3x+47=90.解得x=.故x不是整数，则某一排不可能有90个座位. 11.某城市为了加强公民的节气和用气意识，按以下规定收取每月煤气费：所用煤气如果不超过50m3，按每立方米0.8元收费；如果超过50m3，超过部分按每立方米1.2元收费.设小丽家每月用气量为xm3，应交煤气费为y元. （1）若小丽家某月用煤气量为80m3，则小丽家该月应交煤气费多少元？（2）试写出y与x之间的关系式；（3）若小丽家4月份的煤气费为88元，则她家4月份所用煤气为多少立方米？（4）已知小丽家6月份的煤气费平均每立方米0.95元，那么6月份小丽家用了多少立方米的煤气？ 解：（1）根据题意,得小丽家该月应交煤气费为0.8×50+1.2×（80-50）=76（元）.（2）当x≤50时，y=0.8x；当x＞50时，y=0.8×50+1.2（x-50）=1.2x-20.（3）设小丽家4月份用煤气xm3.因为0.8×50=40（元），而88元＞40元，根据题意，得1.2x-20=88.解得x=90.答：小丽家4月份用煤气90m3. （4）设6月份小丽家用了am3的煤气.根据题意,得1.2a-20=0.95a.解得a=80.答：6月份小丽家用了80m3的煤气.