七年级下数学课件《三角形内角和定理 2 》参考课件2_鲁教版

七年级下数学课件《三角形内角和定理 2 》参考课件2_鲁教版

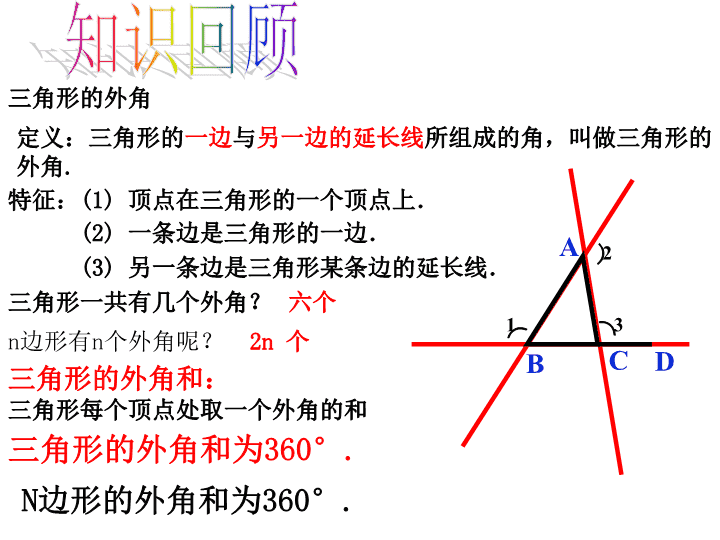
8.6三角形内角和定理（2） 三角形内角和定理三角形三个内角和等于1800.△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:∠A=1800–(∠B+∠C).∠B=1800–(∠A+∠C).∠C=1800–(∠A+∠B).∠A+∠B=1800-∠C.∠B+∠C=1800-∠A.∠A+∠C=1800-∠B.这里的结论,以后可以直接运用.回顾思考☞ABC 特征：(1)顶点在三角形的一个顶点上．(2)一条边是三角形的一边．(3)另一条边是三角形某条边的延长线．三角形的外角定义：三角形的一边与另一边的延长线所组成的角，叫做三角形的外角.DABC三角形一共有几个外角？六个三角形的外角和为360°.知识回顾n边形有n个外角呢？三角形每个顶点处取一个外角的和2n个⌒1⌒2⌒3三角形的外角和：N边形的外角和为360°. 如图.∠1是△ABC的一个外角,∠1与图中的其它角有什么关系?∠1+∠4=1800∠1>∠2，∠1>∠3∠1=∠2+∠3.证明:∵∠2+∠3+∠4=1800(三角形内角和定理),∠1+∠4=1800(平角的意义),∴∠1=∠2+∠3.(等量代换).∴∠1>∠2,∠1>∠3(和大于部分).ABCD1234能证明你的结论吗?三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角. 三角形内角和定理的推论:推论1:三角形的一个外角等于和它不相邻的两个内角的和.推论2:三角形的一个外角大于任何一个和它不相邻的内角.ABCD1234推论：由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.推论可以当作定理使用. 例2已知:如图，在△ABC中,AD平分外角∠EAC,∠B=∠C.求证：AD∥BC.证明：∵∠EAC=∠B+∠C∠B=∠C∴∠DAC=∠C∴AD∥BCACDBE∵AD平分∠EAC∴∠DAC=∠EAC··还有其它方法吗？∴∠C=∠EAC ACDBE··例2已知:如图在△ABC中,AD平分外角∠EAC,∠B=∠C.求证：AD∥BC.∵AD平分∠EAC∴∠DAE=∠EAC∴∠DAE=∠B∴AD∥BC证明：∵∠EAC=∠B+∠C∠B=∠C∴∠B=∠EAC 例3已知:如图,∠BAF,∠CBD,∠ACE是△ABC的三个外角。求证:∠BAF+∠CBD+∠ACE=360°.BACDFE123证明:∵∠BAF是△ABC的一个外角（已知）∴∠BAF=∠2+∠3(三角形的一个外角等于和它不相邻的两个内角的和).同理，∠CBD=∠1+∠3，∠ACE=∠1+∠2.∴∠BAF+∠CBD+∠ACE=2×180°=360°（等量代换）∵（∠1+∠2+∠3）=180°（三角形内角和定理）∴∠BAF+∠CBD+∠ACE=2（∠1+∠2+∠3）（等式的性质） 1、已知：如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.求：∠B和∠ACB的大小.ABCD解：∵∠DCA=∠A+∠B∠DCA=100°,∠A=45°∴∠B=100°-45°=55°又∵∠DCA+∠BCA=180°∴∠ACB=180°-1000=800100°45°练一练 我们知道：“在三角形的每个顶点处各取一个外角，它们的和就是这个三角形的外角和”．（1）三角形的外角和是多少度？（2）如果将三角形三条边都向两边延长，并且在每条线上任取两点连接起来，那么在原三角形外又得到三个新三角形，如图所示，猜想：∠A、∠B、∠C、∠D、∠E、∠F的和是多少？请用（1）的结论证明你的猜想．⌒1⌒2⌒3∠A+∠B+∠C+∠D+∠E+∠F=3600 小结三角形内角和定理：推论1：推论2：推论3：三角形三个内角的和等于1800.三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.直角三角形的两锐角互余.三角形的外角和为360°.N边形的外角和为360°.三角形外角和定理：三角形外角和定理推论：