[精] 华师大版 数学七年级下册 课件 9三角形内角和与外角和

[精] 华师大版 数学七年级下册 课件 9三角形内角和与外角和

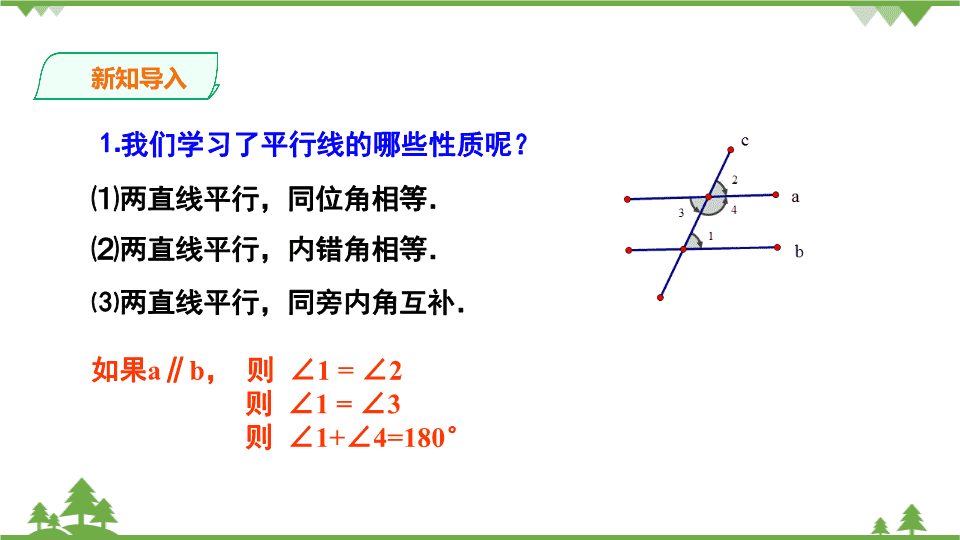
9.1.2三角形内角和与外角和第九章多边形 1.掌握三角形的内角和定理，理解直角三角形的两个锐角互余的性质。2.掌握三角形外角的性质。3.会用三角形的内角与外角的性质来进行相关计算或比较。学习目标 新知导入⒈我们学习了平行线的哪些性质呢？⑴两直线平行，同位角相等．⑵两直线平行，内错角相等．⑶两直线平行，同旁内角互补．如果a∥b，则∠1=∠2则∠1=∠3则∠1+∠4=180° 新知导入请同学们回忆上一节三角形按角分类分为哪几类？想一想，锐角三角形、直角三角形、钝角三角形的三角之和有什么共同特点？锐角三角形;直角三角形;钝角三角形.你是怎样知道的呢？共同特点：三角形的内角和等于180° 撕一撕拼一拼证一证新知讲解 新知讲解你有什么办法可以验证它呢?方法一:剪拼法.把三个角拼在一起试试看？想一想探索1.三角形的内角和. 新知讲解12321图112323图2231如果我们不用剪拼办法，可不可以用说理的办法说明该结论正确呢？ 新知讲解证明:作CE∥AB,并延长BC到D，∴∠1=∠A(两直线平行,内错角相等)∠2=∠B(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°(平角定义)∴∠A+∠B+∠ACB=180°(等量代换)21231已知：∠A，∠B，∠ACB是△ABC的三个内角，证明：∠A+∠B+∠C=180°21EDCBA 新知讲解F21ECBA证明:过点A作EF∥BC∴∠B=∠2，∠C=∠1（两直线平行,内错角相等）∵∠2+∠1+∠BAC=180°（平角定义）∴∠B+∠C+∠BAC=180°(等量代换)已知：∠A，∠B，∠ACB是△ABC的三个内角，证明：∠A+∠B+∠C=180°12332 三角形的内角和定理文字语言：三角形的内角和等于180°符号语言：∵∠A、∠B、∠C是△ABC的三个内角∴∠A＋∠B＋∠C＝180°（三角形的内角和等180°）总结新知讲解直角三角的两个锐角互余 新知讲解在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线。在平面几何里，辅助线通常画成虚线。为了证明三个角的和为180°,转化为一个平角,这种转化思想是数学中的常用方法.思路总结 课堂练习1、在△ABC中，∠A=35°，∠B=43°则∠C=.2、在△ABC中，∠A:∠B:∠C=2:3:4，则∠A=∠B=.∠C=.3、一个三角形中最多有个直角？为什么？4、一个三角形中最多有个钝角？为什么？5、一个三角形中至少有个锐角？为什么？102°80°60°40°211 课堂练习7008003503007006、∠C=(),∠E=(),∠J=().30°115°20°三角形的内角和是180° 新知讲解探索2：三角形的外角与内角有什么关系呢？思考：三角形的一个外角与相邻的内角有什么关系呢？∠ACD(外角)+∠ACB(相邻的内角)=180˚（互补）思考：三角形的一个外角与不相邻的两个内角又有什么关系呢？外角相邻的内角不相邻的内角 在一张白纸上画出如图所示的图形，然后把∠1、∠2剪下拼在一起，放到∠４上，看看会出现什么结果？发现：∠１＋∠２＝∠４新知讲解做一做为什么？ ∠ACD+∠ACB=180°∠A+∠B+∠ACB=180°所以，∠A+∠B=∠ACDABC新知讲解方法1 新知讲解21EDCBA证明:作CE∥AB，并延长BC到D∴∠1=∠A∠2=∠B∴∠1+∠2=∠A+∠B∵∠1+∠2=∠ACD，∴∠ACD=∠A+∠B方法2 新知讲解三角形的一个外角与三角形三个内角之间有何关系？ABCD三角形的一个外角等于与它不相邻的两个内角的和。三角形的外角大于任何一个与它不相邻的内角。∠ACD=∠A+∠B∠ACD+∠ACB=180°三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢？外角+相邻的内角=180˚ 新知讲解与三角形每个内角相邻的外角分别有两个，这两个外角是对顶角，从与每个内角相邻的两个外角中分别取一个相加，得到的和称为三角形的外角和，如图所示∠1+∠2+∠3就是三角形外交和三角形外角和的定义：（1 做一做新知讲解∠1+=180°∠2+=180°∠3+=180°三式相加可以得到∠1+∠2+∠3+++=。①而∠ACB+∠BAC+∠ABC=180°②由①②比较得到∠1+∠2+∠3=360°（1如图所示∠BAC∠ABC∠ACB∠BAC∠ABC∠ACB540°由此可知，三角形的外角和是360° 新知讲解例、D是△ABC的BC边上的一点，∠B=∠BAD,∠ADC=80°，∠BAC=70°求：（1）∠B的度数（2）∠C的度数解:(1)∵∠ADC是△ABD的外角（已知）∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等于与它不相邻的两个内角之和)又∵∠B=∠BAD（已知）∴∠B=80°=40°（等量代换） （2）∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)∴∠C=180°-∠B-∠BAC(等式的性质)=180°-40°-70°=70°例、D是△ABC的BC边上的一点，∠B=∠BAD,∠ADC=80°，∠BAC=70°求：（1）∠B的度数（2）∠C的度数新知讲解 课堂练习7、判断（1）三角形越大，它的内角和就越大。（）（2）一个三角形的三个内角度数是：70°、54°、45°。（）（3）一个三角形中最多只有一个钝角或直角（）（4）一个三角形至少有两个锐角（）（5）三角形的任何一个外角都大于其内角。（）×××√√ 课堂练习8.判断∠1与∠3的大小，并说明理由。∵∠3>∠2,∠2>∠1∴∠3>∠1解：∠3>∠1 课堂练习9、已知△ABC中,∠ABC＝∠C=2∠A,BD是AC边上的高，求∠DBC的度数。（三角形内角和定理）解：设∠A＝x，则∠ABC＝∠C＝2x∴x＋2x＋2x＝180°解得x＝36∴∠C＝2×36°＝72°∴∠DBC＝180°－90°－72°（三角形内角和定理）在△BDC中，∵∠BDC＝90°(三角形高的定义）∴∠DBC＝18° 课堂总结内角和三角形外角与内角间的关系通过本课时的学习，需要我们掌握 作业布置从教材中选择 谢谢