七年级下册数学课件《幂的乘方与积的乘方》 (1)_北师大版

七年级下册数学课件《幂的乘方与积的乘方》 (1)_北师大版

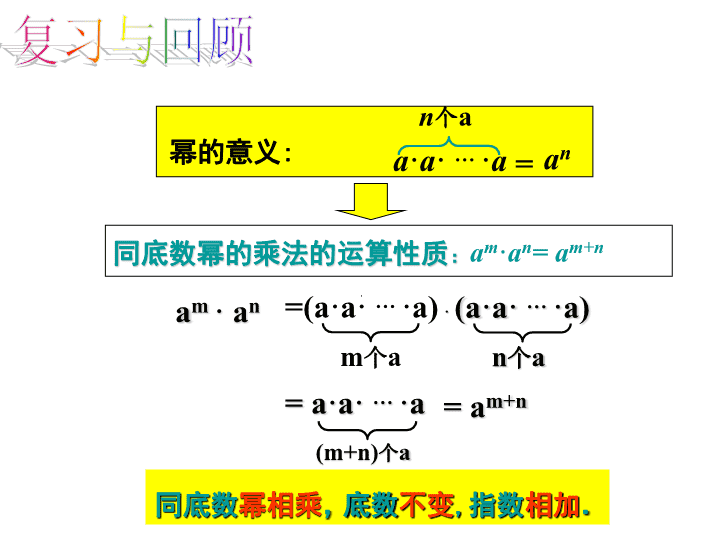
幂的乘方 同底数幂的乘法的运算性质：am·an=(a·a·…·a)m个a=a·a·…·a(m+n)个a=am+nam·an=am+na·a·…·an个aan幂的意义:=同底数幂相乘,底数不变,指数相加.·(a·a·…·a)n个a复习与回顾 （1）；（3）；（5）；（6）.（2）；（4）；1.计算（口答）：2．下面的计算对不对？如果不对应该怎样改正？⑴⑵⑷⑶⑸3．计算：错错对错错 情境引入乙正方体的棱长是2cm,则乙正方体的体积V乙=cm3可以看出，V甲是V乙的倍8125即53倍棱长比的甲正方体的棱长是乙正方体的5倍，则甲正方体的体积V甲=cm31000立方正方体的体积之比= 乙球的半径为3cm,则乙球的体积V乙=cm3.V甲是V乙的倍即103倍球的体积比与半径比的关系甲球的半径是乙球的10倍，则甲球的体积V甲=cm3.10003636000从计算的结果我们看出，球体的体积与半径的大小有着紧密的联系，如果甲球的半径是乙球的n倍，那么甲球的体积是乙球的体积的n3倍.立方球体的体积之比=半径比的 情境引入地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍，它们的体积分别约是地球的多少倍？V球=—πr3，其中V是体积、r是球的半径34103倍(102)3倍你知道(102)3等于多少吗？ 1.2幂的乘方与积的乘方（一）第一章整式的乘除 学习目标1.经历探索幂的乘方的运算性质的过程，进一步体会幂的意义。2.了解幂的乘方的运算性质，并能解决一些简单问题。3.体会类比、归纳等方法的作用，发展运算能力和有条理的思考和表达能力。 探究新知你知道(102)3等于多少吗？(102)3=102×102×102=102+2+2=102×3=106(根据).(根据).同底数幂的乘法幂的意义 个am=am·am·…·am探究新知做一做：计算下列各式，并说明理由.(1)(62)4;(2)(a2)3;(3)(am)2;(4)(am)n.解：(1)(62)4(2)(a2)3(3)(am)2=62·62·62·62=62+2+2+2=68=a2·a2·a2=a2+2+2=a6=am·am=am+m=62×4;(62)4=a2×3;(a2)3=a2m;(am)2n(4)(am)n=amn个m=am+m+…+mn 探究新知幂的乘方，底数，指数.(am)n=amn(m,n都是正整数)不变相乘幂的乘方法则 【例1】计算：(1)(102)3;(2)(b5)5;(3)(an)3;(4)-(x2)m;(5)(y2)3·y;(6)2(a2)6-(a3)4.(6)2(a2)6–(a3)4=102×3=106;(1)(102)3解：(2)(b5)5=b5×5=b25;(3)(an)3=an×3=a3n;(4)-(x2)m=-x2×m=-x2m;(5)(y2)3·y=y2×3·y=y6·y=2a2×6-a3×4=2a12-a12=a12.=y7;例题解析 幂的乘方的逆运算：(1)x13·x7=x（）=()5=()4=()10；(2)a2m=()2=()m（m为正整数）.20x4x5x2ama2幂的乘方法则的逆用 落实基础2.计算：(1)(103)3;(2)－(a2)5;(3)(x3)4·x2;(4)[(－x)2]3;(5)(－a)2(a2)2;(6)x·x4–x2·x3.随堂练习：1.判断下面计算是否正确？如果有错误请改正：(1)(x3)3=x6;(2)a6·a4=a24.相信你准能做对！ 联系拓广⑴a12＝（a3）()＝（a2）()＝a3a()＝（）3＝（）4(4)32﹒9m＝3()(2)y3n＝3,y9n＝.(3)（a2）m+1＝. 想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？ 幂的乘方法则：其中m,n都是正整数.同底数幂的乘法法则： 运算种类公式法则中运算计算结果底数指数同底数幂乘法幂的乘方乘法乘方不变不变指数相加指数相乘 底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m,n都是正整数 1.下列各式对吗？请说出你的观点和理由：(1)(a4)3=a7()(2)a4a3=a12()(3)(a2)3+(a3)2=(a6)2()(4)(－x3)2=(－x2)3()××××达标测评 2．下列各式中，与x5m+1相等的是（　　）（A）（x5)m+1（B）（xm+1)5（C）x·(x5)m（D）x·x5·xmc3．x14不可以写成（　　）（A）x5·(x3)3（B）(－x)·(－x2)·(－x3)·(－x8)（C）(x7)7（D）x3·x4·x5·x2C