七年级数学下册第四章三角形1认识三角形（第2课时三角形的高、中线与角平分线）课件（新版）北师大版

七年级数学下册第四章三角形1认识三角形（第2课时三角形的高、中线与角平分线）课件（新版）北师大版

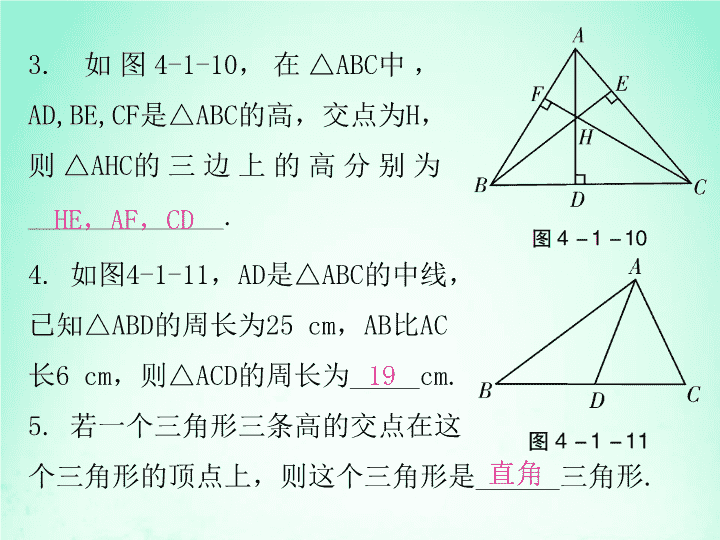
1认识三角形第四章三角形第2课时三角形的高、中线与角平分线 课前预习1.如图4-1-8，AD⊥BC于D，那么图中以AD为高的三角形有__________个.2.如图4-1-9，在△ABC中，AB=13，AC=10，AD为中线，则△ABD与△ACD的周长之差为__________.63 3.如图4-1-10，在△ABC中，AD,BE,CF是△ABC的高，交点为H，则△AHC的三边上的高分别为______________.HE，AF，CD4.如图4-1-11，AD是△ABC的中线，已知△ABD的周长为25cm，AB比AC长6cm，则△ACD的周长为_____cm.5.若一个三角形三条高的交点在这个三角形的顶点上，则这个三角形是______三角形.19直角 课堂讲练典型例题新知1三角形的高【例1】下列四个图形中，线段BE是△ABC的高的是（　）C 【例2】下列尺规作图，能判断AD是△ABC边上的高的是（　）D 模拟演练1.如图4-1-12，△ABC中BC边上的高是（　）A.BDB.AEC.BED.CFB 2.下列各图中，正确画出AC边上的高的是（　）D 典型例题新知2三角形的中线【例3】如图4-1-13，已知△ABC的周长为24cm，AD是BC边上的中线，AD=AB，AD=5cm，△ABD的周长是18cm，求AC的长. 解：因为AD=AB，AD=5cm，所以AB=8cm.又因为△ABD的周长是18cm，所以BD=5cm.又因为D是BC的中点，所以BC=2BD=10cm.又因为△ABC的周长为24cm，所以AC=24-8-10=6（cm）. 【例4】如图4-1-15，在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多5cm，AB与AC的和为13cm，求AC的长.解：因为AD是BC边上的中线，所以D为BC的中点，CD=BD.因为△ADC的周长-△ABD的周长=5,所以AC-AB=5（cm）.又因为AB+AC=13（cm），所以AC=9（cm）,即AC长9cm. 模拟演练3.如图4-1-14，在△ABC中（AB＞BC），AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，求AC和AB的长. 解：因为AD是BC边上的中线，AC=2BC，所以BD=CD.设BD=CD=x，AB=y，则AC=4x，分为两种情况：①AC+CD=60，AB+BD=40，则4x+x=60，x+y=40.解得x=12，y=28.即AC=4x=48，AB=28. ②AC+CD=40，AB+BD=60，则4x+x=40，x+y=60，解得x=8，y=52，即AC=4x=32，AB=52，BC=2x=16.此时不符合三角形三边关系定理,故舍去.综上所述,AC=48，AB=28. 4.如图4-1-16，CD为△ABC的AB边上的中线，△BCD的周长比△ACD的周长大3cm，BC=8cm，求边AC的长.解：因为CD为△ABC的AB边上的中线，所以AD=BD.因为△BCD的周长比△ACD的周长大3cm，所以（BC+BD+CD）-（AC+AD+CD）=3（cm）.所以BC-AC=3（cm）.因为BC=8cm，所以AC=5（cm）. 典型例题新知3三角形的角平分线【例5】如图4-1-17，在△ABC中，∠B=60°，∠C=30°，AD和AE分别是△ABC的高和角平分线，求∠DAE的度数. 解：在△ABC中，∠B=60°，∠C=30°,所以∠BAC=180°-∠B-∠C=180°-60°-30°=90°.因为AE是∠BAC的平分线,所以∠BAE=∠BAC=45°.因为AD是△ABC的高，所以∠ADB=90°.所以在△ADB中，∠BAD=90°-∠B=90°-60°=30°.所以∠DAE=∠BAE-∠BAD=45°-30°=15°. 【例6】如图4-1-19，△ABC中，AD,AE分别是△ABC的高和角平分线，BF是∠ABC的角平分线，BF与AE交于O，若∠ABC=40°，∠C=60°，求∠AEC、∠BOE的度数. 解：在△ABC中，因为∠ABC=40°，∠C=60°，所以∠BAC=180°-∠B-∠C=80°.因为AE是△ABC的角平分线，所以∠EAC=∠BAC=40°.因为AD是△ABC的高，所以∠ADC=90°.所以在△ADC中，∠DAC=180°-∠ADC-∠C=180°-90°-60°=30°.所以∠DAE=∠EAC-∠DAC=40°-30°=10°.所以∠AEC=90°-10°=80°. 因为BF是∠ABC的平分线，所以∠FBC=∠ABC=20°.又因为∠C=60°，所以∠AFO=80°.所以∠AOF=180°-80°-40°=60°.所以∠BOE=∠AOF=60°. 模拟演练5.如图4-1-18，△ABC中，∠ABC=40°，∠C=60°，AD⊥BC于D，AE是∠BAC的平分线.（1）求∠DAE的度数；（2）指出AD是哪几个三角形的高. 解：（1）因为AD⊥BC于D，所以∠ADB=∠ADC=90°.因为∠ABC=40°，∠C=60°，所以∠BAD=50°，∠CAD=30°.所以∠BAC=50°+30°=80°.因为AE是∠BAC的平分线，所以∠BAE=40°.所以∠DAE=50°-40°=10°.（2）AD是△ABE、△ABD、△ABC、△AED、△AEC、△ADC的高. 6.已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD,AC于点F,E，求证：∠CFE=∠CEF. 证明：如答图4-1-1所示标明各角.因为∠ACB=90°，所以∠1+∠3=90°.因为CD⊥AB，所以∠2+∠4=90°.又因为BE平分∠ABC，所以∠1=∠2.所以∠3=∠4.因为∠4=∠5，所以∠3=∠5，即∠CFE=∠CEF. 课后作业新知1三角形的高1.如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（　）A.锐角三角形B.钝角三角形C.直角三角形D.都有可能C 2.画△ABC中AB边上的高，下列画法中正确的是（　）C 3.如图4-1-21，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（　）A.△ABC中，AD是BC边上的高B.△GBC中，CF是BG边上的高C.△ABC中，GC是BC边上的高D.△GBC中，GC是BC边上的高C 新知2三角形的中线4.三角形一边上的中线把原三角形分成两个（　）A.形状相同的三角形B.面积相等的三角形C.直角三角形D.周长相等的三角形B 5.如图4-1-22，在△ABC中，AD是高，AE是∠BAC的平分线，AF是BC边上的中线，则下列线段中，最短的是（　）A.ABB.AEC.ADD.AFC 新知3三角形的角平分线6.如图4-1-23，已知∠1=∠2，∠3=∠4，则正确结论的个数为（　）①AD平分∠BAF；②AF平分∠DAC；③AE平分∠DAF；④AE平分∠BACA.1个B.2个C.3个D.4个B 7.如图4-1-24，在△ABC中，∠C=90°，D，E为AC上的两点，且AE=DE，BD平分∠EBC，则下列说法不正确的是（　）A.BC是△ABE的高B.BE是△ABD的中线C.BD是△EBC的角平分线D.∠ABE=∠EBD=∠DBCD 8.如图4-1-25，若AE是△ABC边BC上的高，AD是∠EAC的平分线交BC于D.若∠ACB=40°，则∠DAE=__________.25° 能力提升9.如图4-1-26，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数. 解：因为∠CAB=50°，∠C=60°,所以∠ABC=180°-50°-60°=70°.又因为AD是高，所以∠ADC=90°.所以∠DAC=180°-90°-∠C=30°.因为AE,BF是角平分线，所以∠CBF=∠ABF=35°，∠EAF=25°.所以∠DAE=∠DAC-∠EAF=5°，∠AFB=∠C+∠CBF=60°+35°=95°.所以∠BOA=∠EAF+∠AFB=25°+95°=120°.故∠DAE=5°，∠BOA=120°.