2020-2021学年浙教 版八年级上册数学期末复习试卷（有答案）

2020-2021学年浙教 版八年级上册数学期末复习试卷（有答案）

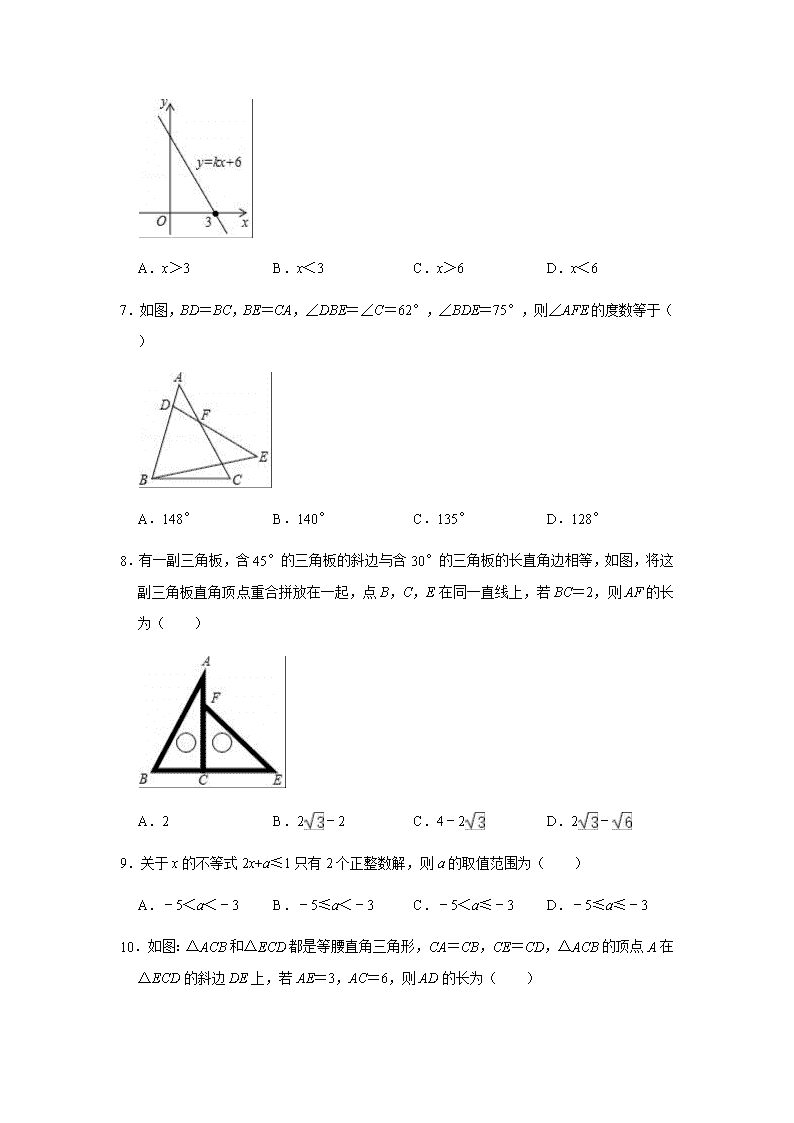
2020-2021学年浙教新版八年级上册数学期末复习试卷一．选择题（共10小题，满分30分，每小题3分）1．49的算术平方根是（　　）A．7B．±7C．﹣7D．2．已知x＞y，则下列不等式不成立的是（　　）A．x﹣6＞y﹣6B．3x＞3yC．﹣2x＜﹣2yD．﹣3x+6＞﹣3y+63．a、b、c为△ABC三边，下列条件不能判断它是直角三角形的是（　　）A．a2＝c2﹣b2B．a＝3，b＝4，c＝5C．∠A：∠B：∠C＝3：4：5D．a＝5k，b＝12k，c＝13k（k为正整数）4．关于一次函数y＝5x﹣3的描述，下列说法正确的是（　　）A．图象经过第一、二、三象限B．向下平移3个单位长度，可得到y＝5xC．函数的图象与x轴的交点坐标是（0，﹣3）D．图象经过点（1，2）5．一个正方形的面积等于30，则它的边长a满足（　　）A．4＜a＜5B．5＜a＜6C．6＜a＜7D．7＜a＜86．如图，直线y＝kx+6经过点（3，0），则关于x的不等式kx+6＜0的解集是（　　） A．x＞3B．x＜3C．x＞6D．x＜67．如图，BD＝BC，BE＝CA，∠DBE＝∠C＝62°，∠BDE＝75°，则∠AFE的度数等于（　　）A．148°B．140°C．135°D．128°8．有一副三角板，含45°的三角板的斜边与含30°的三角板的长直角边相等，如图，将这副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC＝2，则AF的长为（　　）A．2B．2﹣2C．4﹣2D．2﹣9．关于x的不等式2x+a≤1只有2个正整数解，则a的取值范围为（　　）A．﹣5＜a＜﹣3B．﹣5≤a＜﹣3C．﹣5＜a≤﹣3D．﹣5≤a≤﹣310．如图：△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A在△ECD的斜边DE上，若AE＝3，AC＝6，则AD的长为（　　） A．3B．6C．9D．4二．填空题（共6小题，满分24分，每小题4分）11．不等式﹣3x﹣6≥﹣18的正整数解为　　．12．若在实数范围内有意义，则x的取值范围是　　．13．若一个直角三角形的三边分别为x，4，5，则x＝　　．14．|3﹣|﹣＝　　．15．已知关于x，y的方程组的解满足不等式2x+y＞8，则m的取值范围是　　．16．如图，正方形ABCD中，AD＝+2，已知点E是边AB上的一动点（不与A、B重合）将△ADE沿DE对折，点A的对应点为P，当△APB是等腰三角形时，AE＝　　．三．解答题（共8小题，满分66分）17．解不等式组．，把不等式组的解集在数轴上表示出来．18．如图，在△ABC中，AB＝AC＝8，BC＝12，点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动，点E同时从C出发以每秒2个单位的速度在线段CA 上向点A运动，连接AD、DE，设D、E两点运动时间为t秒（0＜t＜4）（1）运动　　秒时，AE＝DC；（2）运动多少秒时，△ABD≌△DCE能成立，并说明理由；（3）若△ABD≌△DCE，∠BAC＝α，则∠ADE＝　　（用含α的式子表示）．19．在如图所示的方格纸中，△ABC的顶点都在小正方形的顶点上，以小正方形互相垂直的两边所在直线建立直角坐标系．（1）作出△ABC关于y轴对称的△A1B1C1，其中点A，B，C分别和点A1，B1，C1对应；（2）平移△ABC，使得点A在x轴上，点B在y轴上，平移后的三角形记为△A2B2C2，作出平移后的△A2B2C2，其中点A，B，C分别和点A2，B2，C2对应；（3）直接写出△ABC的面积．20．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝12，BC＝5，求BD的长． 21．如图，平面直角坐标系中，一次函数y＝﹣x+4的图象l1分别与x，y轴交于A，B两点，正比例函数的图象l2与l1交于点C（m，3）．（1）求m的值及l2的解析式；（2）求S△AOC﹣S△BOC的值；（3）一次函数y＝kx+1的图象为l3，且l1，l2，l3不能围成三角形，直接写出k的值．22．茶为国饮，茶文化是中国传统文化的重要组成部分，这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展，在“春季茶叶节”期间，某茶具店老板购进了A、B两种不同的茶具．若购进A种茶具1套和B种茶具2套，需要250元：若购进A种茶具3套和B种茶具4套则需要600元．（1）A、B两种茶具每套进价分别为多少元？（2）由于茶具畅销，老板决定再次购进A、B两种茶具共80套，茶具工厂对两种类型的茶具进行了价格调整，A种茶具的进价比第一次购进时提高了8%，B种茶具的进价按第一次购进时进价的八折；如果茶具店老板此次用于购进A、B两种茶具的总费用不超过6240元，则最多可购进A种茶具多少套？（3）若销售一套A种茶具，可获利30元，销售一套B种茶具可获利20元，在（2）的条件下，如何进货可使再次购进的茶具获得最大的利润？最大的利润是多少？ 23．如图1，已知直线y＝﹣2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第一象限内作等腰Rt△ABC．（1）求A、B两点的坐标；（2）求BC所在直线的函数关系式；（3）如图2，直线BC交y轴于点D，在直线BC上取一点E，使AE＝AC，AE与x轴相交于点F．①求证：BD＝ED；②在x轴上是否存在一点P，使△APE的面积等于△ABD的面积？若存在，直接写出点P的坐标；若不存在，说明理由．24．如图1，在平面直角坐标系中，直线AB分别交x轴、y轴于点A（a，0）点B（0，b）且a、b满足a2+4a+4+|2a+b|＝0．（1）a＝　　；b＝　　．（2）点P在直线AB的右侧，且∠APB＝45°，①若点P在x轴上，则点P的坐标为　　； ②若△ABP为直角三角形，求点P的坐标；（3）如图2，在（2）的条件下，∠BAP＝90°且点P在第四象限，AP与y轴交于点M，BP与x轴交于点N，连接MN．求证：∠1＝∠2．（提示：过点P作PH⊥AP交x轴于H） 参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．解：72＝49，∴49的算术平方根是7．故选：A．2．解：A、∵x＞y，∴x﹣6＞y﹣6，故本选项错误；B、∵x＞y，∴3x＞3y，故本选项错误；C、∵x＞y，∴﹣x＜﹣y，∴﹣2x＜﹣2y，故选项错误；D、∵x＞y，∴﹣3x＜﹣3y，∴﹣3x+6＜﹣3y+6，故本选项正确．故选：D．3．解：A．若a2＝c2﹣b2，则△ABC为直角三角形，故本选项不合题意；B．若a＝3，b＝4，c＝5，则△ABC为直角三角形，故本选项不合题意；C．若∠A：∠B：∠C＝3：4：5，则最大角∠C＜90°，△ABC不是直角三角形，故本选项符合题意；D．若a＝5k，b＝12k，c＝13k（k为正整数），则a2+b2＝c2，那么这个三角形就是直角三角形，故本选项不合题意．故选：C．4．解：在y＝5x﹣3中，∵5＞0，∴y随x的增大而增大；∵﹣3＜0，∴函数与y轴相交于负半轴， ∴可知函数过第一、三、四象限；向下平移3个单位，函数解析式为y＝5x﹣6；将点（0，﹣3）代入解析式可知，﹣3＝﹣3，函数的图象与y轴的交点坐标是（0，﹣3），将点（1，2）代入解析式可知，2＝5﹣3＝2，故选：D．5．解：∵＜＜，∴5＜＜6．故选：B．6．解：∵x＞3时，y＜0，∴关于x的不等式kx+6＜0的解集是x＞3．故选：A．7．解：∵BD＝BC，BE＝CA，∠DBE＝∠C，∴△ABC≌△EDB（SAS），∴∠A＝∠E，∵∠DBE＝62°，∠BDE＝75°，∴∠E＝180°﹣62°﹣75°＝43°，∴∠A＝43°，∵∠BDE+∠ADE＝180°，∴∠ADE＝105°，∴∠AFE＝∠ADE+∠A＝105°+43°＝148°．故选：A． 8．解：在Rt△ABC中，BC＝2，∠A＝30°，AC＝＝2，则EF＝AC＝2，∵∠E＝45°，∴FC＝EF•sinE＝，∴AF＝AC﹣FC＝2﹣，故选：D．9．解：解不等式2x+a≤1得：x≤，不等式有两个正整数解，一定是1和2，根据题意得：2≤＜3，解得：﹣5＜a≤﹣3．故选：C．10．解：连接BD，∵CA＝CB，CE＝CD，∠ECA＝90°﹣∠ACD＝∠DCB，∴△ECA≌△DCB（SAS），∴DB＝AE＝3，∠CDB＝∠E＝45°，∴∠ADB＝ADC+CDB＝90°，在Rt△ABC中，CA＝CB＝6， ∴AB＝6，在Rt△ADB中，AB＝6，BD＝3，∴AD＝＝＝3故选：A．二．填空题（共6小题，满分24分，每小题4分）11．解：﹣3x﹣6≥﹣18，移项得：﹣3x≥﹣18+6合并同类项得：﹣3x≥﹣12，把x的系数化为1得：x≤4，∴不等式﹣3x﹣6≥﹣18的正整数解为1、2、3、4．故答案为1、2、3、4．12．解：根据题意得x﹣3≥0，解得x≥3．故答案为：x≥3．13．解：设第三边为x，（1）若5是直角边，则第三边x是斜边，由勾股定理得：52+42＝x2，∴x＝；（2）若5是斜边，则第三边x为直角边，由勾股定理得：32+x2＝52，∴x＝3；∴第三边的长为3或． 故答案为：3或．14．解：|3﹣|﹣＝3﹣﹣（﹣3）＝6﹣15．解：解方程组得x＝2m﹣1，y＝4﹣5m，将x＝2m﹣1，y＝4﹣5m代入不等式2x+y＞8得4m﹣2+4﹣5m＞8，∴m＜﹣6，故答案为m＜﹣6．16．解：若AP＝BA，∵四边形ABCD是正方形∴AD＝AB，∠DAB＝90°，∵折叠∴AD＝DP＝AP，∠ADE＝∠PDE∴△ADP是等边三角形∴∠ADP＝60°∴∠ADE＝30°∴AE＝＝若AP＝PB，如图，过点P作PF⊥AD于点F，作∠MED＝∠MDE， ∵AP＝PB，∴点P在AB的垂直平分线上，且PF⊥AD，∴PF＝AB，∵折叠∴AD＝DP＝AB，∠ADE＝∠PDE∴PF＝PD∴∠PDF＝30°∴∠ADE＝15°∵∠MED＝∠MDE，∴∠AME＝30°，ME＝MD∴AM＝AE，ME＝2AE∴AD＝2AE+AE＝2+∴AE＝1当AB＝PB时，∴AB＝AD＝BP，由折叠知，AD＝DP，∴BP＝DP， 在△ADP和△ABP中，，∴△ADP≌△ABP（SSS），∴∠DAP＝∠BAP＝45°，∴∠DAE＝90°，∴点E和点B重合，不符合题意，即：AB＝PB此种情况不存在，故答案为：1或三．解答题（共8小题，满分66分）17．解：解不等式2x+5≤3（x+2），得：x≥﹣1，解不等式2x﹣＜1，得：x＜3，则不等式组的解集为﹣1≤x＜3，将解集表示在数轴上如下：18．解：（1）由题可得，BD＝CE＝2t，∴CD＝12﹣2t，AE＝8﹣2t，∴当AE＝DC，时，8﹣2t＝（12﹣2t），解得t＝3，故答案为：3；（2）当△ABD≌△DCE成立时，AB＝CD＝8， ∴12﹣2t＝8，解得t＝2，∴运动2秒时，△ABD≌△DCE能成立；（3）当△ABD≌△DCE时，∠CDE＝∠BAD，又∵∠ADE＝180°﹣∠CDE﹣∠ADB，∠B＝∠180°﹣∠BAD﹣∠ADB，∴∠ADE＝∠B，又∵∠BAC＝α，AB＝AC，∴∠ADE＝∠B＝（180°﹣α）＝90°﹣α．故答案为：90°﹣α．19．解：（1）如图所示，△A1B1C1即为所求． （2）如图所示，△A2B2C2即为所求．（3）△ABC的面积为3×3﹣×1×3﹣×1×2﹣×2×3＝．20．解：∵在Rt△ABC中，∠ACB＝90°，AC＝12，BC＝5，∴AB＝＝13，∵AB•CD＝AC•BC∴CD＝＝，∴BD＝＝．21．解：（1）一次函数y＝﹣x+4的图象l1分别与x，y轴交于A，B两点，则点A、B的坐标分别为：（8，0）、（0，4），则OA＝8，OB＝4，将点C坐标代入上式得：3＝﹣m+4，解得：m＝2，点C（2，3），设l2的表达式为：y＝nx，将点C（2，3）代入上式得：3＝2n，解得：n＝，故：l2的表达式为：y＝x；（2）S△AOC﹣S△BOC＝×OA×yCBO×xC＝×8×3×4×2＝8； （3）当l1∥l3或l2∥l3时，l1，l2，l3不能围成三角形，即k＝﹣或，当l3过点C时，将点C坐标代入上式并解得：k＝1；故当l3的表达式为：y＝x+1或y＝x+1或y＝x+1．故k＝﹣或或1．22．解：（1）设A种茶具每套进价x元，B两种茶具每套进价y元，依题意得：，解得：，答：A、B两种茶具每套进价分别为100元和75元．（2）设最多购进A种茶具a套，则B套茶具（80﹣a）套，依题意得：100（1+8%）a+75×80%（80﹣a）≤6240．解得：a≤30．∵a取正整数，∴0＜a≤30．∴a的最大值为30．答：最多可购进A种茶具30套．（3）设茶具的利润为w，则依题意得：w＝30a+20（80﹣a）＝10a+1600，又∵0＜a≤30，∴w随a的增大而增大，∴当a＝30时，W＝10×30+1600＝1900元． 即采购A种茶具30个，B种茶具50个可获得最利润为1900元．答：最大利润为1900元．23．解：（1）y＝﹣2x+2中，当x＝0时y＝2，则A（0，2），当y＝0时，﹣2x+2＝0，解得x＝1，则B（1，0）；（2）如图①，过点C作CD⊥x轴于点D，则∠AOB＝∠BDC＝90°，∴∠OAB+∠ABO＝90°，∵△ABC是等腰直角三角形，∴AB＝BC，∠ABC＝90°，∴∠ABO+∠CBD＝90°，∴∠OAB＝∠DBC，∴△ABO≌△BCD（AAS），∴BD＝OA＝2，CD＝OB＝1，则点C（3，1）， 设直线BC所在直线解析式为y＝kx+b，将点B（1，0）、C（3，1）代入，得：，解得，∴直线BC所在直线解析式为y＝x﹣．（3）①过点C作CG⊥x轴于点G，作EM⊥x轴于点M，EN⊥y轴于点N，则∠BGC＝∠BME＝∠END＝∠BOD＝90°，∵∠ABC＝90°，且AE＝AC，∴AB是CE的中垂线，∴BC＝BE，∵∠CBG＝∠EBM，∴△BCG≌△BEM（AAS），∴BM＝BG＝2，EM＝CG＝1，∵BO＝1，∴OM＝EN＝OB＝1， ∵∠BDO＝∠EDN，∴△BDO≌△EDN（AAS），∴BD＝ED；②如图③，作EH⊥x轴于点H，由y＝x﹣知D（0，﹣），即OD＝，则AD＝OA+OD＝，∴S△ABD＝AD•OB＝××1＝，由①知E（﹣1，﹣1），根据A（0，2）、E（﹣1，﹣1）得直线AE解析式为y＝3x+2，当y＝0时，3x+2＝0，解得x＝﹣，∴F（﹣，0），设P（a，0），∴PF＝|﹣﹣a|，则S△APE＝S△APF+S△EPF＝•PF•（EH+AO） ＝•|﹣﹣a|•3＝|+a|，∵S△ABD＝S△APE，∴|+a|＝，解得a＝或a＝﹣，∴点P的坐标为（，0）或（﹣，0）．24．解：（1）a2+4a+4+|2a+b|＝（a+2）2+|2a+b|＝0，即：a＝﹣2，b＝4，故答案是﹣2，4；（2）①点P在x轴上，则OP＝OB＝4，故：答案是（4，0）；②当∠BAP＝90°时，∠HAP+∠BAH＝90°，∠ABO+∠HPA＝90°，∴∠OBA＝∠HAP，∠ABO＝∠AHP＝90°，又∠APB＝45°，∴AP＝AB，∴△AOB≌△AHP（AAS），∴PH＝AO＝2，AH＝OB＝4，OH＝AH﹣AO＝2， 故点P的坐标为（2，﹣2）；当∠ABP＝90°时，同理可得：点P的坐标为（4，2），故点P的坐标为（2，﹣2）或（4，2）；（3）过点P作PH⊥AP交x轴于H，过点P分别作x、y轴的垂线，交于点F、E，由（2）知，PE＝PF＝2，∠MPE+∠NPF＝∠EPF﹣∠MPN＝90°﹣45°＝45°，∠HPF+∠FPN＝∠MPH﹣∠MPN＝90°﹣45°＝45°，∴∠MPE＝∠HPF，又∠HFP＝∠MEP＝90°，∴△MEP≌△HFP（AAS），∴∠2＝∠FHP，MP＝HP，∠HPN＝∠HPF+∠FPN＝∠MPE+∠FPN＝45°＝∠MPN，又PN＝PN，∴△MNP≌△HNP（SAS），∴∠1＝∠NHP，∴∠1＝∠2．