- 2022-03-31 发布 |
- 37.5 KB |
- 18页

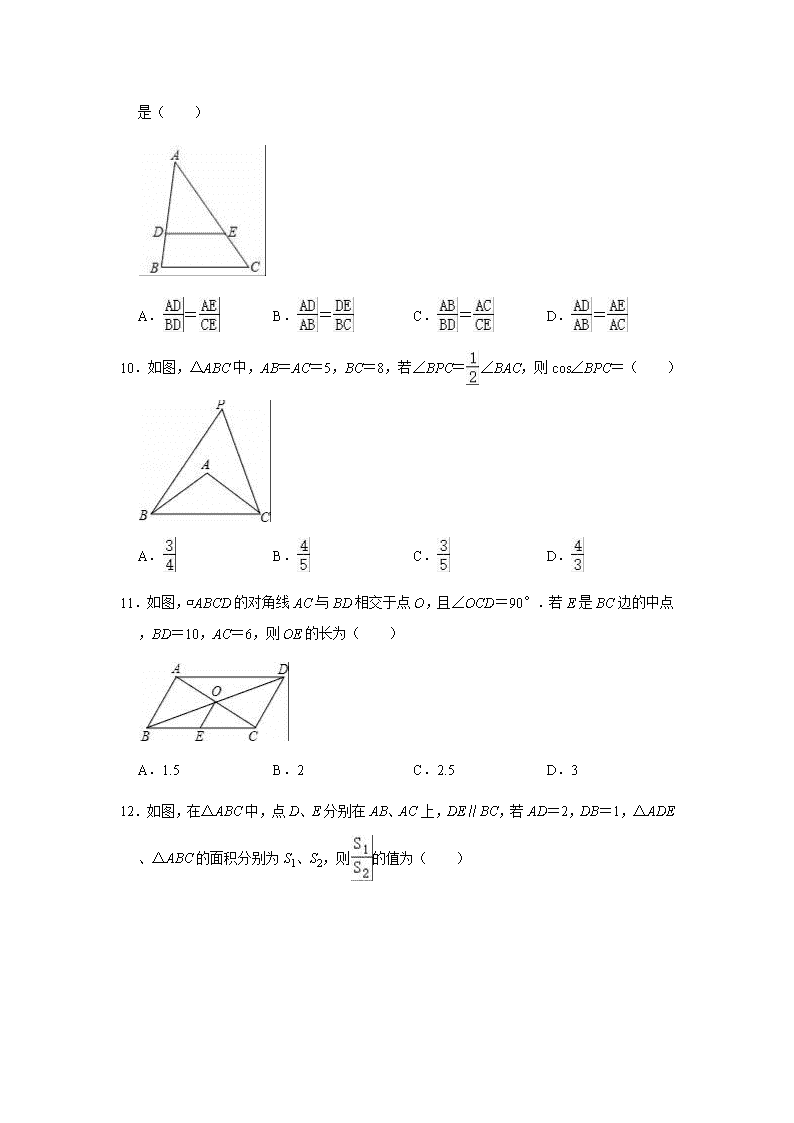
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020-2021学年华东师大 版九年级上册数学期末复习试卷1
2020-2021学年华东师大新版九年级上册数学期末复习试卷1一.选择题(共14小题,满分42分,每小题3分)1.若=x﹣5,则x的取值范围是( )A.x<5B.x≤5C.x≥5D.x>52.下列计算中,正确的是( )A.B.C.D.3.下列计算:(1)()2=2,(2)=2,(3)(﹣2)2=12,(4)(+1)(﹣1)=1.其中结果正确的个数为( )A.1B.2C.3D.44.若代数式有意义,则x的取值范围是( )A.x>﹣1且x≠1B.x≥﹣1C.x≠1D.x≥﹣1且x≠15.方程x2=4x的根是( )A.x=4B.x=0C.x1=0,x2=4D.x1=0,x2=﹣46.已知x=﹣2是方程x2+bx﹣2=0的一个根,则b的值为( )A.1B.﹣1C.2D.﹣27.将一元二次方程x2﹣8x﹣5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是( )A.﹣4,21B.﹣4,11C.4,21D.﹣8,698.某厂通过改进工艺降低了某种产品的成本,两个月内从每件产品250元降低到每件160元,则平均每月降低的百分率为( )A.10%B.5%C.15%D.20%9.如图,点D、E分别在△ABC的边AB、AC上,下列各比例式不一定能推得DE∥BC 的是( )A.=B.=C.=D.=10.如图,△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,则cos∠BPC=( )A.B.C.D.11.如图,▱ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )A.1.5B.2C.2.5D.312.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若AD=2,DB=1,△ADE、△ABC的面积分别为S1、S2,则的值为( ) A.B.C.D.213.如图,一张三角形纸片ABC,其中∠C=90°,AC=6,BC=8.某同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m、n的长度分别是( )A.4,B.4,3C.4,D.3,514.如图,在山地上种树,已知∠A=30°,AC=3米,则相邻两株树的坡面距离AB是( )A.6米B.米C.2米D.2米二.填空题(共4小题,满分16分,每小题4分)15.(4分)若x<2,化简﹣|4﹣x|的结果是 .16.(4分)如果关于x的一元二次方程x2﹣3x+k=0有两个相等的实数根,那么实数k的值是 .17.(4分)如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形 ABCD的面积是12,那么阴影部分的面积是 .18.(4分)如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F,若BC=4,∠CBD=30°,则DF的长为 .三.解答题(共6小题,满分62分)19.(14分)计算:20.(8分)某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元.经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.(1)降价后,每件衬衫的利润为 元,销量为 件;(用含x的式子表示)(2)为了扩大销售,尽快减少库存,商场决定采取降价措施.但需要平均每天盈利1200元,求每件衬衫应降价多少元?21.(8分)在甲口袋中有三个球分别标有数码1,﹣2,3;在乙口袋中也有三个球分别标有数码4,﹣5,6;已知口袋均不透明,六个球除标码不同外其他均相同,小明从甲口袋中任取一个球,并记下数码,小林从乙口袋中任取一个球,并记下数码.(1)用树状图或列表法表示所有可能的结果;(2)求所抽取的两个球数码的乘积为负数的概率.22.(9分)如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少? 23.(10分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,1)、B(1,﹣2)、C(3,﹣1).(1)画出△A1B1C1,使△A1B1C1与△ABC关于点O成中心对称,并写出点A的对应点A1的坐标 ;(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△ABC放大后的△A2B2C2,并写出点A的对应点A2的坐标 ;(3)sin∠B2A2C2= .24.(13分)在矩形ABCD中,AB=a,AD=b,点E为对角线AC上一点,连接DE,以DE为边,作矩形DEFG,点F在边BC上;(1)观察猜想:如图1,当a=b时,= ,∠ACG= ;(2)类比探究:如图2,当a≠b时,求的值(用含a、b的式子表示)及∠ACG的度数; (3)拓展应用:如图3,当a=6,b=8,且DF⊥AC,垂足为H,求CG的长. 参考答案与试题解析一.选择题(共14小题,满分42分,每小题3分)1.解:∵=x﹣5,∴5﹣x≤0∴x≥5.故选:C.2.解:A、==3,故本选项正确;B、与不是同类二次根式不能合并,故本选项错误;C、3×3=9,故本选项错误;D、=3,故本选项错误.故选:A.3.解:(1)()2=2,结果正确;(2)=2,结果正确;(3)(﹣2)2=12,结果正确;(4)(+1)(﹣1)=()2﹣12=2﹣1=1,结果正确;故选:D.4.解:由题意得:x+1≥0,且x﹣1≠0,解得:x≥﹣1,且x≠1,故选:D.5.解:方程整理得:x(x﹣4)=0,可得x=0或x﹣4=0, 解得:x1=0,x2=4,故选:C.6.解:把x=﹣2是方程x2+bx﹣2=0得4﹣2b﹣2=0,解得b=1.故选:A.7.解:∵x2﹣8x﹣5=0,∴x2﹣8x=5,则x2﹣8x+16=5+16,即(x﹣4)2=21,∴a=﹣4,b=21,故选:A.8.解:如果设平均每月降低率为x,根据题意可得250(1﹣x)2=160,∴x1=20%,x2=180%(不合题意,舍去).故选:D.9.解:∵,∴DE∥BC,∵,∴DE∥BC,∵,∴DE∥BC,故选:B. 10.解:过点A作AE⊥BC于点E,如图所示:∵AB=AC=5,∴BE=BC=×8=4,∠BAE=∠BAC,∵∠BPC=∠BAC,∴∠BPC=∠BAE.在Rt△BAE中,由勾股定理得AE===3,∴cos∠BPC=cos∠BAE==.故选:C.11.解:∵四边形ABCD是平行四边形,BD=10,AC=6,∴OA=3,OB=5,AB∥DC,∵∠OCD=90°,∴∠BAO=90°,∴AB=,∵E是BC边的中点,OA=OC,∴2OE=AB,∴OE=2, 故选:B.12.解:∵DE∥BC,∴△ADE∽△ABC,∴=()2=,故选:C.13.解:如图所示:由折叠的性质得:DE是线段AC的垂直平分线,∴DE是△ABC的中位线,∴m=DE=BC=4;∵∠C=90°,AC=6,BC=8,∴AB===10,由折叠的性质得:AD=BD=AB=5,∠BDF=90°,∵∠B=∠B,∴△BDF∽△BCA,∴,即,解得:DF=,即n=,故选:A. 14.解:cos30°=,∴AB=2.故选:C.二.填空题(共4小题,满分16分,每小题4分)15.解:∵x<2,∴﹣|4﹣x|=|x﹣2|﹣(4﹣x)=2﹣x﹣4+x=﹣2.故答案为:﹣2.16.解:根据题意得△=(﹣3)2﹣4k=0,解得k=.故答案为.17.解:∵四边形ABCD是矩形,∴AB∥CD,OA=OC,∴∠EAO=∠FCO,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴S△AOE=S△COF,∴S阴=S△COD=S矩形ABCD=3, 故答案为:3.18.解:如图,在Rt△BDC中,BC=4,∠DBC=30°,∴BD=2,连接DE,∵∠BDC=90°,点E是BC中点,∴DE=BE=CE=BC=2,∵∠DCB=30°,∴∠BDE=∠DBC=30°,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠BDE,∴DE∥AB,∴△DEF∽△BAF,∴,∴.解得:DF=.故答案为:. 三.解答题(共6小题,满分62分)19.解:原式=4×﹣(﹣)+2﹣+2×=2﹣3++2﹣+2=4﹣1.20.解:(1)∵每件衬衫降价x元,∴每件衬衫的利润为(40﹣x)元,销量为(20+2x)件.故答案为:(40﹣x);(20+2x).(2)依题意,得:(40﹣x)(20+2x)=1200,整理,得:x2﹣30x+200=0,解得:x1=10,x2=20.∵为了扩大销售,增加盈利,尽快减少库存,∴x=20.答:每件衬衫应降价20元.21.解:(1)列表如下:1﹣234(1,4)(﹣2,4)(3,4)﹣5(1,﹣5)(﹣2,﹣5)(3,﹣5)6(1,6)(﹣2,6)(3,6)(2)由表可知,共有9种等可能结果,其中所抽取的两个球数码的乘积为负数的由4种结果,∴所抽取的两个球数码的乘积为负数的概率为.22.解:如图:延长AB. ∵CD∥AB,∴∠CAB=30°,∠CBF=60°;∴∠BCA=60°﹣30°=30°,即∠BAC=∠BCA;∴BC=AB=3米;Rt△BCF中,BC=3米,∠CBF=60°;∴BF=BC=1.5米;故x=BF﹣EF=1.5﹣0.8=0.7米.答:这时汽车车头与斑马线的距离x是0.7米.23.解:(1)如图,△A1B1C1即为所求,A1(﹣2,﹣1);故答案为:(﹣2,﹣1);(2)如图,△A2B2C2即为所求,A2(﹣4,﹣2);故答案为:(﹣4,﹣2); (3)由题可得,△A2B2C2为等腰直角三角形,∴∠B2A2C2=45°,∴,故答案为:.24.解:(1)如图1,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,∵a=b,∴AB=AD,∴矩形ABCD是正方形,∴∠ACD=∠DAE=45°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN=∠MEF,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴EF=DE.∵四边形DEFG是矩形, ∴矩形DEFG是正方形;∵四边形ABCD是正方形,∴DE=DG,AD=DC,∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG.∠DAE=∠DCG=45°,∴=1,∠ACG=∠ACD+∠DCG=90°,故答案为:1;90°;(2)如图2,作EM⊥BC于M,EN⊥CD于N,则EM∥AB,EN∥AD,四边形EMCN是矩形,∴EM:AB=CE:AC,EN:AD=CE:AC,∠MEN=90°,∴EM:AB=EN:AD,∴==,∵四边形ABCD、四边形DEFG是矩形,∴∠ADC=∠DEF=∠EDG=90°,∴∠DEN=∠FEM,∠ADE=∠CDG,∵∠END=∠EMF=90°,∴△DEN∽△FEM,∴===, ∴△ADE∽△CDG,∴==,∠DAE=∠DCG,∵AB∥CD,∴∠BAC=∠ACD,∵∠BAC+∠DAE=90°,∴∠ACD+∠DCG=90°,即∠ACG=90°;(3)∵a=6,b=8,∴CD=AB=6,BC=AD=8,∴AC==10,∵DF⊥AC,∴DH===,∴CH===,∵∠FHC=∠B=90°,∠FCH=∠ACB,∴△CFH∽△CAB,∴=,即=,解得:FH=,∴DF=DH+FH=,由(2)得:===,设DE=4x,则EF=3x,∵∠DEF=90°, ∴DF==5x=,∴x=,∴DE=4x=6=DC,∴EH=CH,∴CE=2CH=,∴AE=AC﹣CE=10﹣=,由(2)得:====,∴CG=AE=.查看更多