七年级下册数学课件《完全平方公式 完全平方公式的认识》 (7)_北师大版

七年级下册数学课件《完全平方公式 完全平方公式的认识》 (7)_北师大版

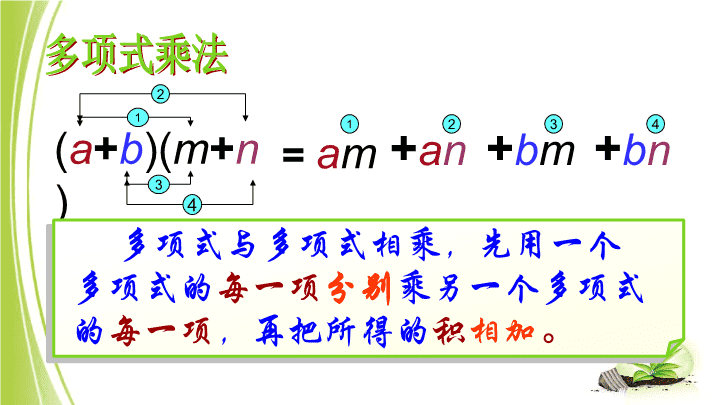
欢迎光临 124(a+b)(m+n)=am1234+an+bm+bn3多项式乘法多项式与多项式相乘，先用一个多项式的每一项分别乘另一个多项式的每一项，再把所得的积相加。 计算(x+3)(x+2)(x+5)(x-7)(x+3)(x+3)(3x+2)2(m+2n)2(a+b)2观察左边的算式及其计算结果，你有什么发现？=a2+2ab+b2(x+3)2 (a+b)2=a2+2ab+b2仿照平方差公式你能用自己的语言叙述这一公式吗？如果把公式中的b换成-b，你又能得到什么？(-b)(-b)(-b)(a-b)2=a2-2ab+b2完全平方公式：语言描述：两数和（或差）的平方，等于这两数的平方和加上（或减去）这两数积的两倍. 结构特点：首平方,尾平方,两倍乘积放中央,符号看前方(a+b)2=a2+2ab+b2(a－b)2=a2－2ab+b2(首±尾)2=首2±2首尾+尾2左边是二项式（两数和（差））的平方；右边是一个三项式即两数的平方和加上（减去）这两数乘积的两倍. 练习1.明辨是非，知错能改。①(a+1)2=a2+1（）②(a－1)2=a2－1（）③(2a－1)2=2a2－2a+1（）④(a－2)2=a2－4a－4（）××××a2+1+2aa2+1－2a(2a)2－2×2a+1a2－4a+4 例1利用完全平方公式计算：(2x−3)2；(a-b)2=a2-2ab+b232x2x3(-)2=()2-2··+()22x3=4x2-12x+9 计算(a+b)22.(a-b)23.(-a+b)23.(-a-b)2练习2.利用公式进行计算1.(x+4)22.(2t-1)23.(7a+2)2首平方,尾平方,两倍乘积放中央,符号同加异减 (-1-2x)2=(-1)2-2·(-1)·2x+(2x)2=1+4x+4x2=(-1)2+2·(-1)·(-2x)+(-2x)2=1+4x+4x2=(1+2x)2=1+4x+4x2(a-b)2=a2-2ab+b2(a+b)2=a2+2ab+b2还有其他方法吗？方法2：(-1-2x)2方法3：(-1-2x)2(a+b)2=a2+2ab+b2=[-(1+2x)]2(-1-2x)2完全平方公式再识例2计算： (2)(-4x-5y)2;(3)(mn−a)2(2)(-4x-5y)2=(-4x)2+2·(-4x)·(-5y)+(-5y)2=16x2+40xy+25y2(3)(mn-a)2=(mn)2-2·mn·a+a2=m2n2-2amn+a2 1.教材习题1.11.2.拓展练习：(a+b)2与(a－b)2有怎样的联系？能否用一个等式来表示两者之间的关系，并尝试用图形来验证你的结论？3.阅读P24杨辉三角探究(a+b)3、(a+b)4…(a+b)n作业 小结注意完全平方公式和平方差公式不同：形式不同．结果不同：完全平方公式的结果是三项，即(ab)2＝a22ab+b2;平方差公式的结果是两项，即(a+b)(a−b)＝a2−b2.有时需要进行变形，使变形后的式子符合应用完全平方公式的条件，即为“两数和(或差)的平方”，然后应用公式计算.在解题过程中要准确确定a和b、对照公式原形的两边,做到不丢项、不弄错符号、2ab时不少乘2；首尾是分数或数字与字母的乘积，平方时要注意添括号