七年级下册数学课件《整式的除法》 (6)_北师大版

七年级下册数学课件《整式的除法》 (6)_北师大版

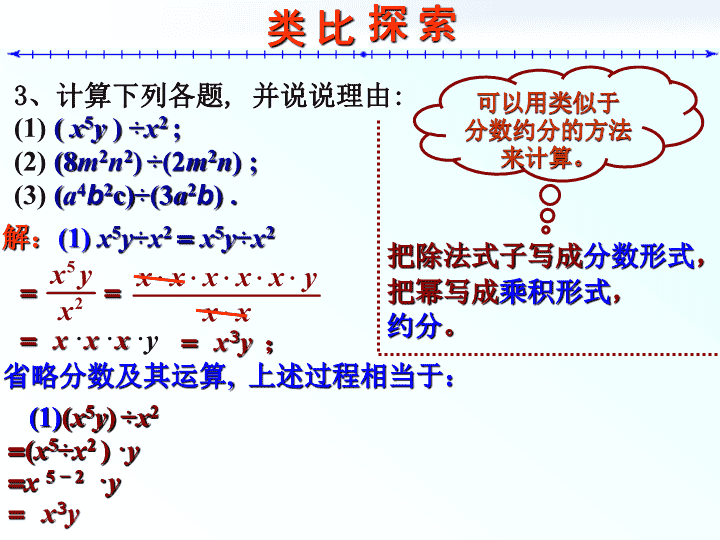
7标题标题《数学》(北师大.七年级下册)第一章整式整式的除法(1) 类比探索3、计算下列各题,并说说理由:(1)(x5y)÷x2;(2)(8m2n2)÷(2m2n);(3)(a4b2c)÷(3a2b).解：(1)x5y÷x2=x5y÷x2把除法式子写成分数形式，=把幂写成乘积形式，约分。==x·x·x·y=x3y；省略分数及其运算,上述过程相当于：(1)(x5y)÷x2=(x5÷x2)·y=x5−2·y可以用类似于分数约分的方法来计算。探索(1)(x5y)÷x2=(x5÷x2)·y=x5−2·y=x3y (1)(x5y)÷x2=x5−2·y(2)(8m2n2)÷(2m2n)=(8÷2)·m2−2·n2−1;(3)(a4b2c)÷(3a2b)=(1÷3)·a4−2·b2−1·c.观察&归纳商式被除式除式仔细观察一下，并分析与思考下列几点：(被除式的系数)÷(除式的系数)写在商里面作(被除式的指数)—(除式的指数)商式的系数＝单项式除以单项式，其结果(商式)仍是：被除式里单独有的幂，(同底数幂)商的指数＝一个单项式？因式。 单项式的除法法则如何进行单项式除以单项式的运算?单项式相除,把系数、同底数的幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连它的指数一起作为商的一个因式。理解商式＝系数•同底的幂•被除式里单独有的幂底数不变，指数相减。保留在商里作为因式。 例题解析例题例1计算：(1);(2)(10a4b3c2)÷(5a3bc);(−x2y3)÷(3x2y3)(3)(2x2y)3·(−7xy2)÷(14x4y3);(4)(2a+b)4÷(2a+b)2.本例所涉及的知识点：（1）同底幂的除法法则:am÷an=am−n（2）括号内是积、括号外右角有指数时，先用积的乘方法则。（3）两个底数是相同的多项式时,应看成一个整体. 解： 注意运算顺序：先乘方，再乘除，最后算加减可以把看成一个整体 答:学以致用月球距离地球大约3.84×105千米,一架飞机的速度约为8×102千米/时.如果乘坐此飞机飞行这么远的距离,大约需要多少时间?3.84×105÷(8×102)？这样列式的依据=0.48×103？如何得到的？单位是什么=480(小时)？如何得到的=20(天).？做完了吗如果乘坐此飞机飞行这么远的距离,大约需要20天时间.解题后的反思你能直接列出一个时间为天的算式吗?3.84×105÷(8×102)÷12.你会计算吗? 本节课你的收获是什么？小结在计算题时，要注意运算顺序和符号．同底数幂相除是单项式除法的特例；单项式除以单项式的法则的探求过程中我们使用了观察、归纳的方法，这是数学发现规律的一种常用方法。 单项式相乘单项式相除第一步第二步第三步系数相乘系数相除同底数幂相乘同底数幂相除其余字母不变连同其指数作为积的因式只在被除式里含有的字母连同其指数一起作为商的因式对比学习