2019-2020学年山东省济南市天桥区七年级（下）期末数学试卷

2019-2020学年山东省济南市天桥区七年级（下）期末数学试卷

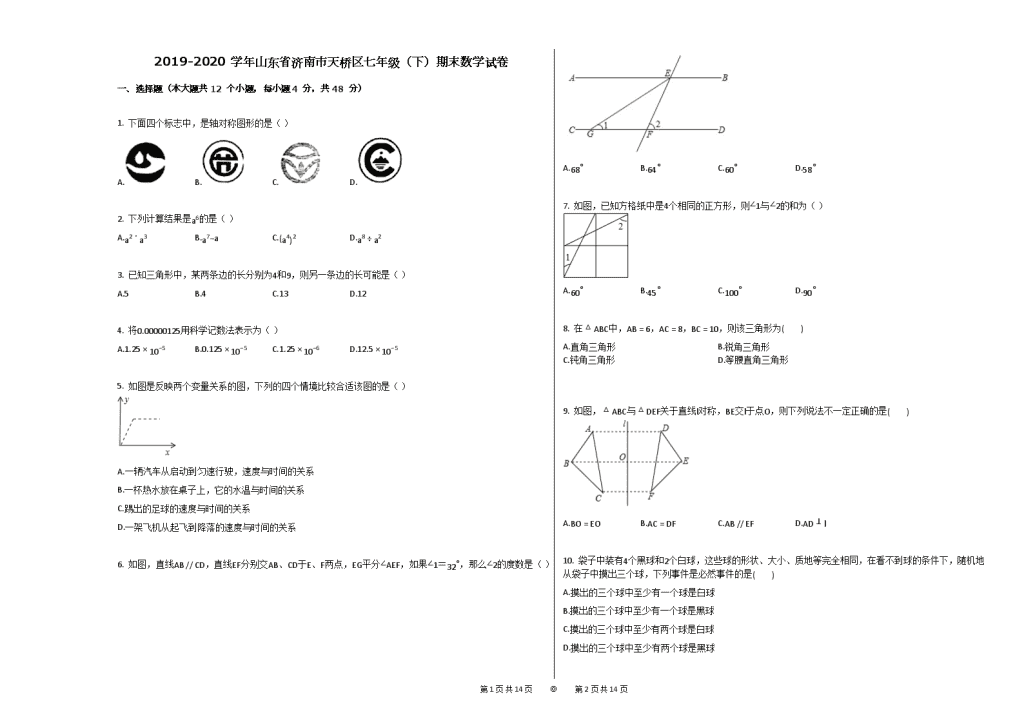
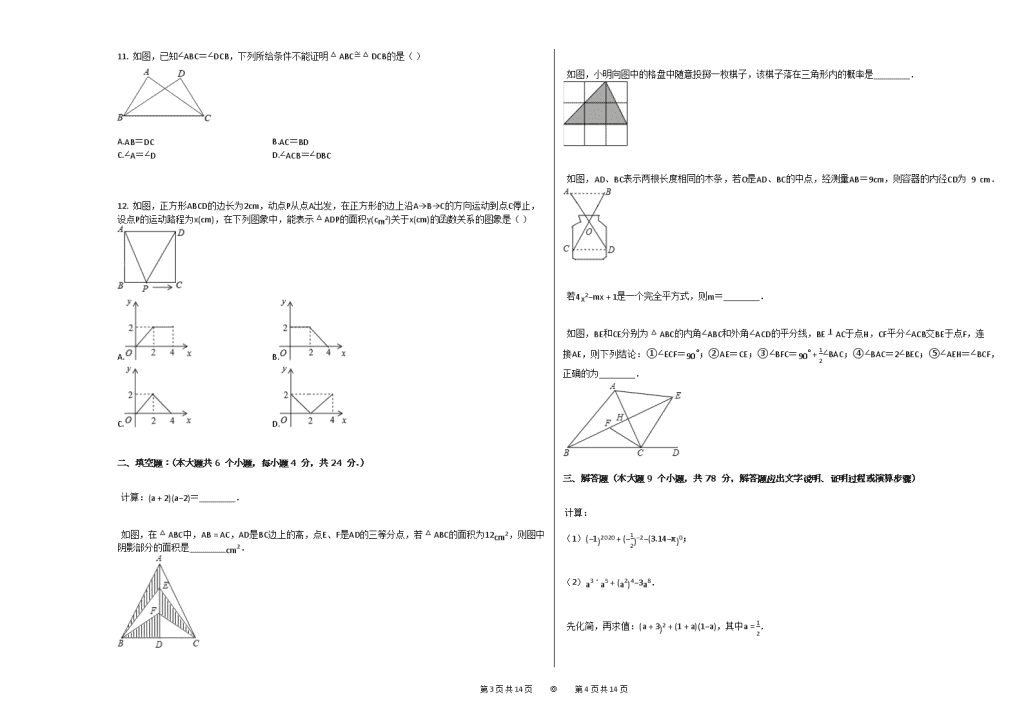
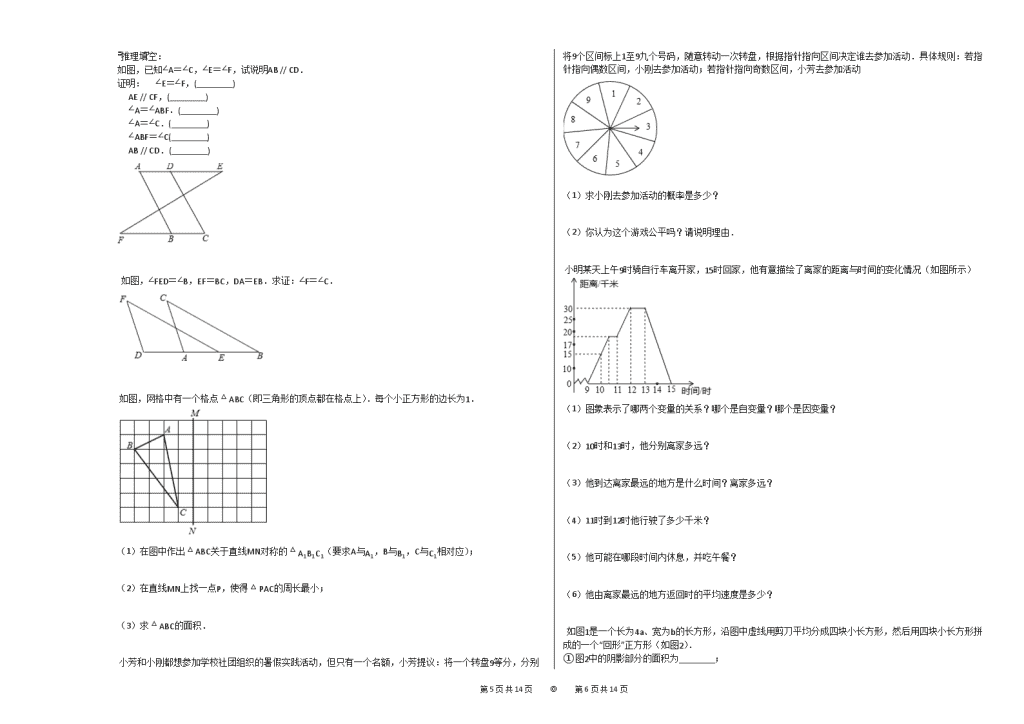
‎2019-2020学年山东省济南市天桥区七年级（下）期末数学试卷 一、选择题（本大题共12个小题，每小题4分，共48分）‎ ‎ ‎ ‎1. 下面四个标志中，是轴对称图形的是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎2. 下列计算结果是a‎6‎的是（ ） ‎ A.a‎2‎‎⋅‎a‎3‎ B.a‎7‎‎−a C.‎(‎a‎4‎‎)‎‎2‎ D.‎a‎8‎‎÷‎a‎2‎ ‎ ‎ ‎3. 已知三角形中，某两条边的长分别为‎4‎和‎9‎，则另一条边的长可能是（ ） ‎ A.‎5‎ B.‎4‎ C.‎13‎ D.‎‎12‎ ‎ ‎ ‎4. 将‎0.00000125‎用科学记数法表示为（ ） ‎ A.‎1.25×‎‎10‎‎−5‎ B.‎0.125×‎‎10‎‎−5‎ C.‎1.25×‎‎10‎‎−6‎ D.‎‎12.5×‎‎10‎‎−5‎ ‎ ‎ ‎5. 如图是反映两个变量关系的图，下列的四个情境比较合适该图的是（ ） ‎ A.一辆汽车从启动到匀速行驶，速度与时间的关系 B.一杯热水放在桌子上，它的水温与时间的关系 C.踢出的足球的速度与时间的关系 D.一架飞机从起飞到降落的速度与时间的关系 ‎ ‎ ‎6. 如图，直线AB // CD，直线EF分别交AB、CD于E、F两点，EG平分‎∠AEF，如果‎∠1‎＝‎32‎‎∘‎，那么‎∠2‎的度数是（ ） ‎ A.‎68‎‎∘‎ B.‎64‎‎∘‎ C.‎60‎‎∘‎ D.‎‎58‎‎∘‎ ‎ ‎ ‎7. 如图，已知方格纸中是‎4‎个相同的正方形，则‎∠1‎与‎∠2‎的和为（ ） ‎ A.‎60‎‎∘‎ B.‎45‎‎∘‎ C.‎100‎‎∘‎ D.‎‎90‎‎∘‎ ‎ ‎ ‎8. 在‎△ABC中，AB=6‎，AC=8‎，BC=10‎，则该三角形为(        ) ‎ A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰直角三角形 ‎ ‎ ‎ ‎9. 如图，‎△ABC与‎△DEF关于直线l对称，BE交l于点O，则下列说法不一定正确的是‎(‎        ‎)‎ ‎ A.BO‎=‎EO B.AC‎=‎DF C.AB // EF D.‎AD⊥l ‎ ‎ ‎10. 袋子中装有‎4‎个黑球和‎2‎个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是必然事件的是‎(‎        ‎)‎ ‎ A.摸出的三个球中至少有一个球是白球 B.摸出的三个球中至少有一个球是黑球 C.摸出的三个球中至少有两个球是白球 D.摸出的三个球中至少有两个球是黑球 ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎11. 如图，已知‎∠ABC＝‎∠DCB，下列所给条件不能证明‎△ABC≅△DCB的是（ ） ‎ A.AB＝DC B.AC＝BD C.‎∠A＝‎∠D D.‎∠ACB＝‎∠DBC ‎ ‎ ‎ ‎12. 如图，正方形ABCD的边长为‎2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x(cm)‎，在下列图象中，能表示‎△ADP的面积y(cm‎2‎)‎关于x(cm)‎的函数关系的图象是（ ） ‎ A. B. C. D. ‎ 二、填空题：（本大题共6个小题，每小题4分，共24分．）‎ ‎ ‎ ‎ 计算：‎(a+2)(a−2)‎＝________． ‎ ‎ ‎ ‎ 如图，在‎△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若‎△ABC的面积为‎12‎cm‎2‎，则图中阴影部分的面积是________cm‎2‎． ‎ ‎ ‎ ‎ 如图，小明向图中的格盘中随意投掷一枚棋子，该棋子落在三角形内的概率是________． ‎ ‎ ‎ ‎ 如图，AD、BC表示两根长度相同的木条，若O是AD、BC的中点，经测量AB＝‎9cm，则容器的内径CD为 ‎9‎ cm． ‎ ‎ ‎ ‎ 若‎4x‎2‎−mx+1‎是一个完全平方式，则m＝________． ‎ ‎ ‎ ‎ 如图，BE和CE分别为‎△ABC的内角‎∠ABC和外角‎∠ACD的平分线，BE⊥AC于点H，CF平分‎∠ACB交BE于点F，连接AE，则下列结论：①‎∠ECF＝‎90‎‎∘‎；②AE＝CE；③‎∠BFC＝‎90‎‎∘‎‎+‎1‎‎2‎∠BAC；④‎∠BAC＝‎2∠BEC；⑤‎∠AEH＝‎∠BCF，正确的为________． ‎ 三、解答题（本大题9个小题，共78分，解答题应出文字说明、证明过程或演算步骤）‎ ‎ ‎ ‎ 计算： ‎ ‎（1）‎(−1‎)‎‎2020‎+(−‎1‎‎2‎‎)‎‎−2‎−(3.14−π‎)‎‎0‎；‎ ‎ ‎ ‎（2）a‎3‎‎⋅a‎5‎+(a‎2‎‎)‎‎4‎−3‎a‎8‎．‎ ‎ ‎ ‎ 先化简，再求值：‎(a+3‎)‎‎2‎+(1+a)(1−a)‎，其中a=‎‎1‎‎2‎． ‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 推理填空： 如图，已知‎∠A＝‎∠C，‎∠E＝‎∠F，试说明AB // CD． 证明：∵ ‎∠E＝‎∠F，‎(‎________‎)‎ ∴ AE // CF，‎(‎________‎)‎ ∴ ‎∠A＝‎∠ABF．‎(‎________‎)‎ ∵ ‎∠A＝‎∠C．‎(‎________‎)‎ ∴ ‎∠ABF＝‎∠C(‎________‎)‎ ∴ AB // CD．‎(‎________‎)‎ ‎ ‎ ‎ ‎ 如图，‎∠FED＝‎∠B，EF＝BC，DA＝EB．求证：‎∠F＝‎∠C． ‎ ‎ ‎ ‎ 如图，网格中有一个格点‎△ABC（即三角形的顶点都在格点上）．每个小正方形的边长为‎1‎． ‎ ‎（1）在图中作出‎△ABC关于直线MN对称的‎△‎A‎1‎B‎1‎C‎1‎（要求A与A‎1‎，B与B‎1‎，C与C‎1‎相对应）；‎ ‎ ‎ ‎（2）在直线MN上找一点P，使得‎△PAC的周长最小；‎ ‎ ‎ ‎（3）求‎△ABC的面积．‎ ‎ ‎ ‎ 小芳和小刚都想参加学校社团组织的暑假实践活动，但只有一个名额，小芳提议：将一个转盘‎9‎等分，分别将‎9‎个区间标上‎1‎至‎9‎九个号码，随意转动一次转盘，根据指针指向区间决定谁去参加活动．具体规则：若指针指向偶数区间，小刚去参加活动；若指针指向奇数区间，小芳去参加活动 ‎ ‎（1）求小刚去参加活动的概率是多少？‎ ‎ ‎ ‎（2）你认为这个游戏公平吗？请说明理由．‎ ‎ ‎ ‎ 小明某天上午‎9‎时骑自行车离开家，‎15‎时回家，他有意描绘了离家的距离与时间的变化情况（如图所示） ‎ ‎（1）图象表示了哪两个变量的关系？哪个是自变量？哪个是因变量？‎ ‎ ‎ ‎（2）‎10‎时和‎13‎时，他分别离家多远？‎ ‎ ‎ ‎（3）他到达离家最远的地方是什么时间？离家多远？‎ ‎ ‎ ‎（4）‎11‎时到‎12‎时他行驶了多少千米？‎ ‎ ‎ ‎（5）他可能在哪段时间内休息，并吃午餐？‎ ‎ ‎ ‎（6）他由离家最远的地方返回时的平均速度是多少？‎ ‎ ‎ ‎ 如图‎1‎是一个长为‎4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图‎2‎）． ①图‎2‎中的阴影部分的面积为________； ‎ 第13页 共14页 ◎ 第14页 共14页 ‎②观察图‎2‎请你写出 ‎(a+b‎)‎‎2‎、‎(a−b‎)‎‎2‎、ab之间的等量关系是________； ③根据（2）中的结论，若x+y＝‎5‎，x⋅y=‎‎9‎‎4‎，则‎(x−y‎)‎‎2‎＝________； ④实际上通过计算图形的面积可以探求相应的等式． 如图‎3‎，你发现的等式是________． ‎ ‎ ‎ ‎ 如图①，在‎△ABC中，‎∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为直角边且在AD的上方作等腰直角三角形ADF，连接CF． ‎ ‎（1）若AB＝AC，‎∠BAC＝‎90‎‎∘‎ ①当点D在线段BC上时（与点B不重合），试探究CF与BD的数量关系和位置关系，并说明理由． ②当点D在线段BC的延长线上时，①中的结论是否仍然成立，请在图②中画出相应图形并直接写出你的猜想．‎ ‎ ‎ ‎（2）如图③，若AB≠AC，‎∠BAC≠‎‎90‎‎∘‎，‎∠BCA＝‎45‎‎∘‎，点D在线段BC上运动，试探究CF与BC的位置关系，并说明理由．‎ 第13页 共14页 ◎ 第14页 共14页 参考答案与试题解析 ‎2019-2020学年山东省济南市天桥区七年级（下）期末数学试卷 一、选择题（本大题共12个小题，每小题4分，共48分）‎ ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 轴正算图形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 幂的乘表与型的乘方 同底射空的除法 同底水水的乘法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 三角常三簧关系 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 科学表数法擦-老示映小的数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函表的透象 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行体的省质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全正知形 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 勾股定体的展定理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎9.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 轴对验流性质 全等三表形木判定 ‎【解析】‎ 此题暂无解析 第13页 共14页 ◎ 第14页 共14页 ‎【解答】‎ 此题暂无解答 ‎10.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 必水明件 随验把件 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎11.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全等三表形木判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎12.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 动表问擦 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题：（本大题共6个小题，每小题4分，共24分．）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平使差香式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等体三火暗服判定与性质 轴对验流性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 几来锰率 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全等三于形的视用 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 完表平病式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 角平较线的停质 等体三火暗服判定与性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题（本大题9个小题，共78分，解答题应出文字说明、证明过程或演算步骤）‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 零因优幂 幂的乘表与型的乘方 负整明指养幂 第13页 共14页 ◎ 第14页 共14页 同底水水的乘法 实因归运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 整式使以教运算球化简求值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平行线明判轮与性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 全根三烛形做给质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 作图-射对称变面 勾体定展 轴明称月去最键路线问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 游水于平性 概水常式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函表的透象 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 完都证香令式的几何背景 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 三角使如合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第13页 共14页 ◎ 第14页 共14页