认识三角形　（二）教案

认识三角形　（二）教案

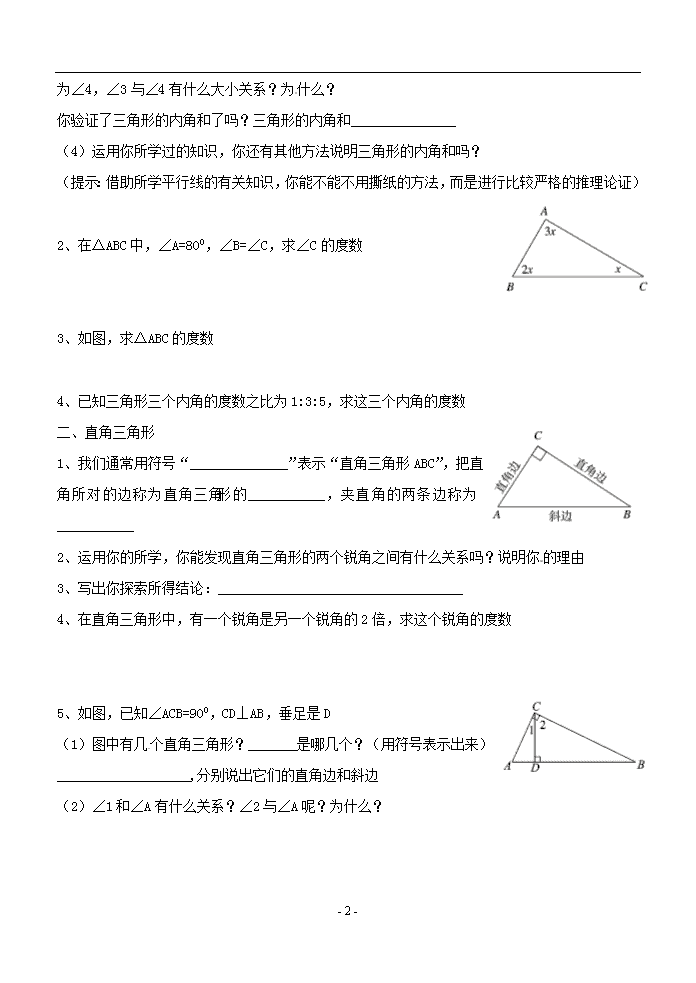
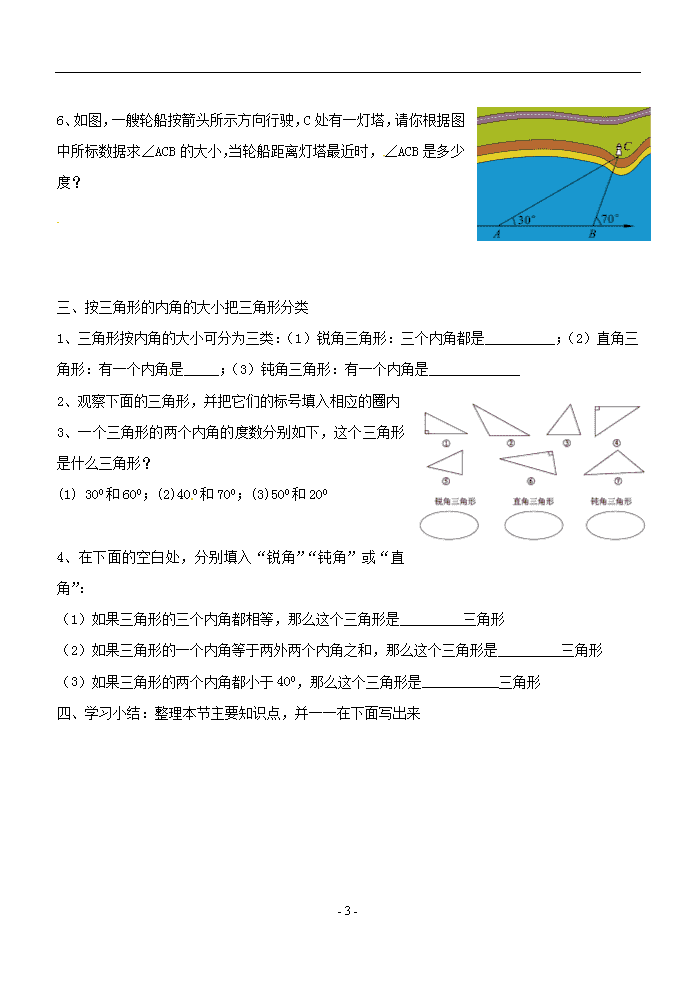
‎ ‎ 认识三角形（二）‎ 班级________姓名________‎ 一、学习目标与要求：‎ 经历实验活动的过程，得出“三角形内角和等于180°”；能从“三角形内角和等于180°”中探索出直角三角形两锐角互余的性质；能应用三角形内角和等于180°来解决一些简单的求三角形内角和问题；会按角的大小关系对三角形分类；能从所给出的已知角中，判断出三角形的形状。‎ 二、重点与难点：‎ 重点：三角形内角和定理及与三角形内角和定理有关结论的理解与掌握 难点：发展推理能力和有条理地表达能力 三、学习过程：‎ 复习回顾：1、三角形任意两边之和__________；任意两边之差___________‎ ‎2、如图，图中共有_______个三角形，用适当的方法把它们一一表示出来 ‎3、已知两条线段的长为5cm和8cm，要钉成一个三角形，试求：‎ ‎（1）第三边的长度范围 ‎（2）若第三条线段长为奇数，求三角形的周长 探索发现：一、三角形的内角和 ‎1、在小学中我们已经知道了，将一个三角形的三个角撕下来，拼在一起可以得到一个平角，于是我们得到了三角形的内角和为1800，现在请你按下面的步骤亲自动手做一做 ‎（1）自己制作几个三角形纸片，如右图，它的三个内角分别为∠1、∠2、∠3‎ ‎（2）将∠1撕下，按图（2）所示进行摆放，其中∠1的顶点与∠2的顶点重合，它的一条边与∠2的一条边重合，此时∠1的另一条边b与∠3的边a平行吗？为什么？‎ ‎（3）如图（3）所示，将∠3与∠‎ - 3 -‎ ‎ ‎ ‎2的公共边延长，它与b所夹的角为∠4，∠3与∠4有什么大小关系？为什么？‎ 你验证了三角形的内角和了吗？三角形的内角和_______________‎ ‎（4）运用你所学过的知识，你还有其他方法说明三角形的内角和吗？‎ ‎（提示：借助所学平行线的有关知识，你能不能不用撕纸的方法，而是进行比较严格的推理论证）‎ ‎2、在ΔABC中，∠A=800，∠B=∠C，求∠C的度数 ‎3、如图，求ΔABC的度数 ‎4、已知三角形三个内角的度数之比为1:3:5，求这三个内角的度数 二、直角三角形 ‎1、我们通常用符号“______________”表示“直角三角形ABC”，把直角所对的边称为直角三角形的___________，夹直角的两条边称为___________‎ ‎2、运用你的所学，你能发现直角三角形的两个锐角之间有什么关系吗？说明你的理由 ‎3、写出你探索所得结论：___________________________________‎ ‎4、在直角三角形中，有一个锐角是另一个锐角的2倍，求这个锐角的度数 ‎5、如图，已知∠ACB=900，CD⊥AB，垂足是D ‎（1）图中有几个直角三角形？_______是哪几个？（用符号表示出来）___________________,分别说出它们的直角边和斜边 ‎（2）∠1和∠A有什么关系？∠2与∠A呢？为什么？‎ - 3 -‎ ‎ ‎ ‎6、如图，一艘轮船按箭头所示方向行驶，C处有一灯塔，请你根据图中所标数据求∠ACB的大小，当轮船距离灯塔最近时，∠ACB是多少度？‎ 三、按三角形的内角的大小把三角形分类 ‎1、三角形按内角的大小可分为三类：（1）锐角三角形：三个内角都是__________；（2）直角三角形：有一个内角是_____；（3）钝角三角形：有一个内角是_____________‎ ‎2、观察下面的三角形，并把它们的标号填入相应的圈内 ‎3、一个三角形的两个内角的度数分别如下，这个三角形是什么三角形？‎ ‎(1) 300和600；(2)400和700；(3)500和200‎ ‎4、在下面的空白处，分别填入“锐角”“钝角”或“直角”：‎ ‎（1）如果三角形的三个内角都相等，那么这个三角形是_________三角形 ‎（2）如果三角形的一个内角等于两外两个内角之和，那么这个三角形是_________三角形 ‎（3）如果三角形的两个内角都小于400，那么这个三角形是___________三角形 四、学习小结：整理本节主要知识点，并一一在下面写出来 - 3 -‎