2019七年级数学上册 第7章 期末复习（无答案）

2019七年级数学上册 第7章 期末复习（无答案）

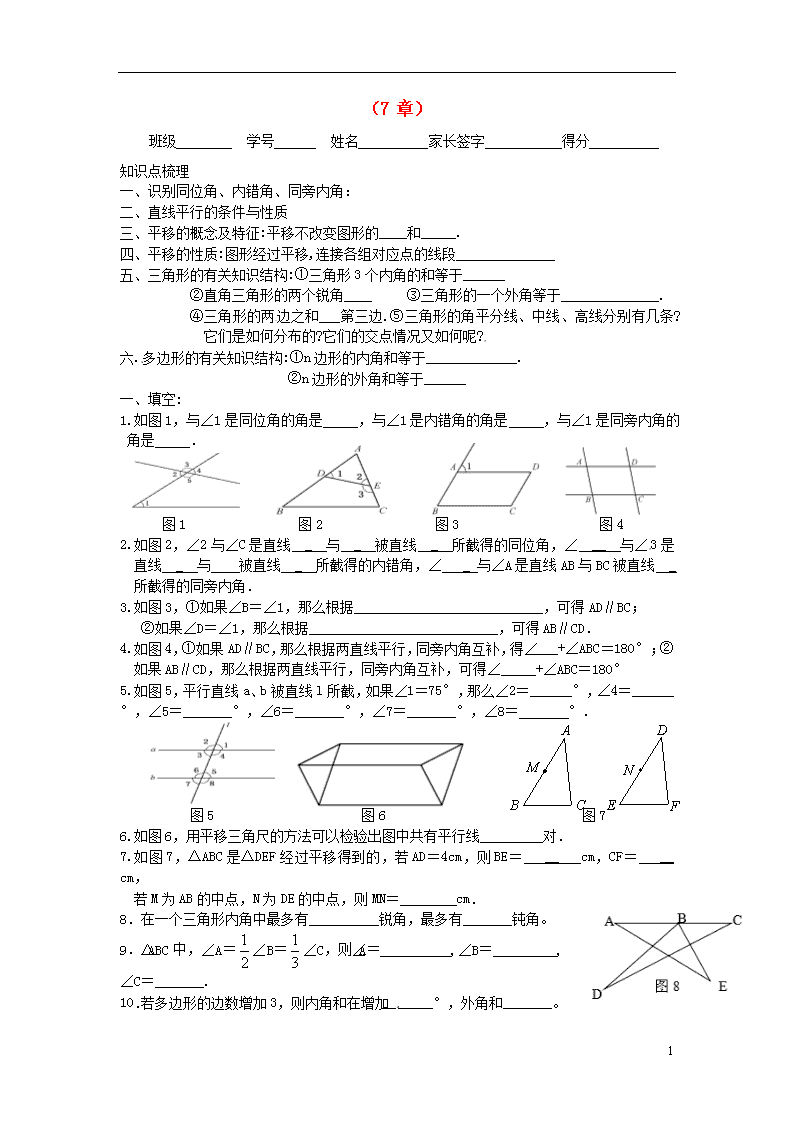
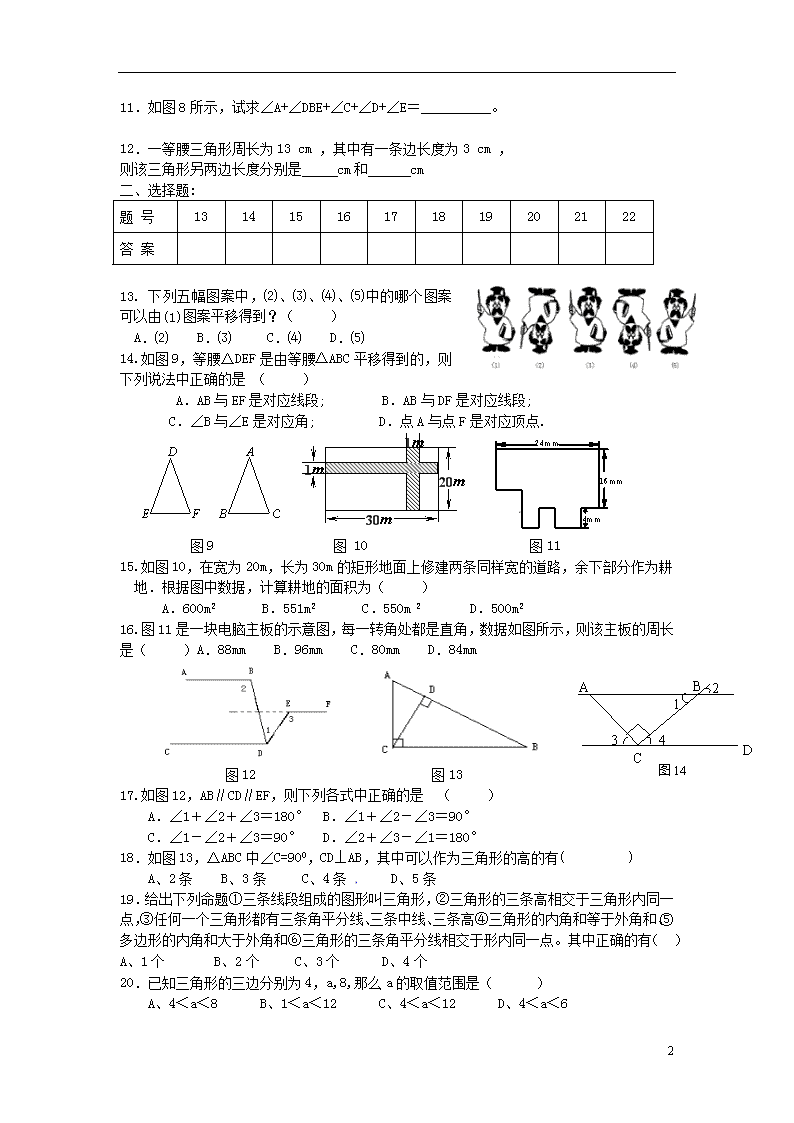
‎（7章）‎ ‎ 班级________ 学号______ 姓名__________家长签字 得分__________‎ 知识点梳理 一、识别同位角、内错角、同旁内角：‎ 二、直线平行的条件与性质 ‎ 三、平移的概念及特征:平移不改变图形的____和_____.‎ 四、平移的性质:图形经过平移,连接各组对应点的线段 ‎ 五、三角形的有关知识结构:①三角形3个内角的和等于______‎ ‎②直角三角形的两个锐角____ ③三角形的一个外角等于______________.‎ ‎④三角形的两边之和___第三边.⑤三角形的角平分线、中线、高线分别有几条?它们是如何分布的?它们的交点情况又如何呢?‎ 六.多边形的有关知识结构:①n边形的内角和等于_____________.‎ ‎②n边形的外角和等于______‎ 一、填空:‎ ‎1.如图1，与∠1是同位角的角是 ，与∠1是内错角的角是 ，与∠1是同旁内角的角是 ．‎ ‎ ‎ 图1 图2 图3 图4 ‎ ‎2.如图2，∠2与∠C是直线 _ 与 _ 被直线 _ 所截得的同位角，∠ __ 与∠3是直线 _ 与 被直线 _ 所截得的内错角，∠ _ 与∠A是直线AB与BC被直线 _ 所截得的同旁内角．‎ ‎3.如图3，①如果∠B＝∠1，那么根据___________________________，可得AD∥BC；‎ ‎②如果∠D＝∠1，那么根据___________________________，可得AB∥CD．‎ ‎4.如图4，①如果AD∥BC，那么根据两直线平行，同旁内角互补，得∠___+∠ABC＝180°；②如果AB∥CD，那么根据两直线平行，同旁内角互补，可得∠_____+∠ABC＝180°‎ ‎5.如图5，平行直线a、b被直线l所截，如果∠1＝75°，那么∠2＝______°，∠4＝______°，∠5＝_______°，∠6＝_______°，∠7＝_______°，∠8＝ °．‎ 图5 图6 图7‎ ‎6.如图6，用平移三角尺的方法可以检验出图中共有平行线_________对．‎ ‎7.如图7，△ABC是△DEF经过平移得到的，若AD＝‎4cm，则BE＝ __ cm，CF＝ __ cm，‎ 若M为AB的中点，N为DE的中点，则MN＝ cm． ‎ ‎8．在一个三角形内角中最多有__________锐角，最多有_______钝角。‎ ‎9．△ABC中，∠A＝∠B＝∠C，则∠A＝__________,∠B＝_________,∠C＝_______.‎ ‎10．若多边形的边数增加3，则内角和在增加_______°，外角和_______。‎ 4‎ ‎11．如图8所示，试求∠A+∠DBE+∠C+∠D+∠E＝__________。‎ ‎12．一等腰三角形周长为‎13 cm ，其中有一条边长度为‎3 cm ，‎ 则该三角形另两边长度分别是 cm和 cm 二、选择题: ‎ 题 号 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ 答 案 13. 下列五幅图案中，⑵、⑶、⑷、⑸中的哪个图案可以由(1)图案平移得到？（ ）‎ A．⑵ B．⑶ C．⑷ D．⑸‎ ‎14.如图9，等腰△DEF是由等腰△ABC平移得到的，则下列说法中正确的是 （ ）‎ A．AB与EF是对应线段; B．AB与DF是对应线段;‎ C．∠B与∠E是对应角; D．点A与点F是对应顶点.‎ ‎1m ‎1m ‎30m ‎20m ‎ ‎ ‎ 图9 图 10 图11‎ ‎15.如图10，在宽为‎20m，长为‎30m的矩形地面上修建两条同样宽的道路，余下部分作为耕地．根据图中数据，计算耕地的面积为（ ）‎ A．‎600m2‎ B．‎551m‎2‎ C．‎550m 2 D．‎‎500m2‎ ‎16.图11是一块电脑主板的示意图，每一转角处都是直角，数据如图所示，则该主板的周长 是（ ）A．‎88mm B．‎96mm C．‎80mm D．‎‎84mm B C A D ‎1‎ ‎2‎ ‎3‎ ‎4‎ 图14‎ ‎ ‎ ‎ 图12 图13‎ ‎17.如图12，AB∥CD∥EF，则下列各式中正确的是 （ ）  ‎ A．∠1＋∠2＋∠3＝180° B．∠1＋∠2－∠3＝90°‎ C．∠1－∠2＋∠3＝90° D．∠2＋∠3－∠1＝180°‎ ‎18．如图13，△ABC中∠C=900，CD⊥AB，其中可以作为三角形的高的有( )‎ A、2条 B、3条 C、4条 D、5条 ‎19．给出下列命题①三条线段组成的图形叫三角形，②三角形的三条高相交于三角形内同一点，③任何一个三角形都有三条角平分线、三条中线、三条高④三角形的内角和等于外角和、⑤多边形的内角和大于外角和⑥三角形的三条角平分线相交于形内同一点。其中正确的有（ ）A、1个 B、2个 C、3个 D、4个 ‎20．已知三角形的三边分别为4，a,8,那么a的取值范围是（ ）‎ A、4＜a＜8 B、1＜a＜‎12 C、4＜a＜12 D、4＜a＜6‎ 4‎ ‎21．有a、b、c、d四根木棒长度分别为4、5、6、9，从中任意选取三根首尾顺次连接围成不同的三角形，则可以围成的三角形共有（ ）‎ A、1个 B、2个 C、3个 D、4个 ‎22．如图14，AB∥CD，AC⊥BC，则图中与∠CAB互余的角有（ ）A、1个 B、2个 C、3个 D、4个 三、作图题：‎ ‎23. 如图，请你根据图中的信息，把小船ABCD 通过平移后到的位置，‎ 画出平移后的小船位置．‎ A B C ‎ ‎ ‎24．画出钝角△ABC的高AD，角平分线BE，中线CF。‎ 四、解答题：‎ ‎25.如图，如果AB//CD，∠B=37°，∠D=37°，那么BC与DE平行吗? 为什么？‎ ‎26.如图，AD//BC，∠A＝∠C．AB与DC平行吗？为什么？‎ ‎27．一个多边形的每一个内角都等于144°，求它的边数。‎ ‎28．一多边形内角和为2340°，若每一个内角都相等，求每个外角的度数。‎ ‎29.如图，在△ABC中，∠A＝40°，∠B＝72°，CD是AB边上的高，CE是∠ACB的平分线，DF⊥CE于F，求∠CDF的度数.‎ 4‎ 五、拓展题：‎ ‎30.如图，已知直线 ∥，且 和、分别交于A、B 两点，点P在直线AB上．‎ ‎（1）试找出∠1、∠2、∠3之间的关系并说明理由；‎ ‎（2）当点P在A、B两点之间运动时，问∠1、∠2、∠3之间的关系是否发生变化？‎ A P B ‎1‎ ‎2‎ ‎3‎ ‎（3）如果点P在A、B两点外侧运动时，试探究∠1、∠2、∠3 之间的关系（点P和A、B不重合，只要写出结论，不要证明）‎ ‎31.现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°．‎ ‎①将这两块三角板摆成如图a的形式，使B、F、E、A在同一条直线上，点C在边DF上，DE与AC相交于点G， 试求∠AGD的度数．‎ D A E F B C G E A F B C D a b ‎②将图a中的△ABC固定，把△DEF绕着点F逆时针旋转成如图b的形式，当旋转的角度等于多少度时，DF∥AC？并说明理由．‎ ‎32.如图（1）△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点，‎ 研究（1）：如果沿直线DE折叠，则∠BDA′与∠A的关系是_____ __。‎ 研究（2）：如果折成图2的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由。‎ 研究（3）：如果折成图3的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由。‎ A A′‎ B E D C 图3‎ C B A A′‎ D E 图2‎ A A′‎ B E D C 图1‎ 4‎