高一数学必修5课件-3一元二次不等式 及其解法
课前练习
2.比较大小
3 2 5;
1 5 2
3 2
(1) + 7
(2)
<
<
3.2.1 一元二次不等式
及其解法
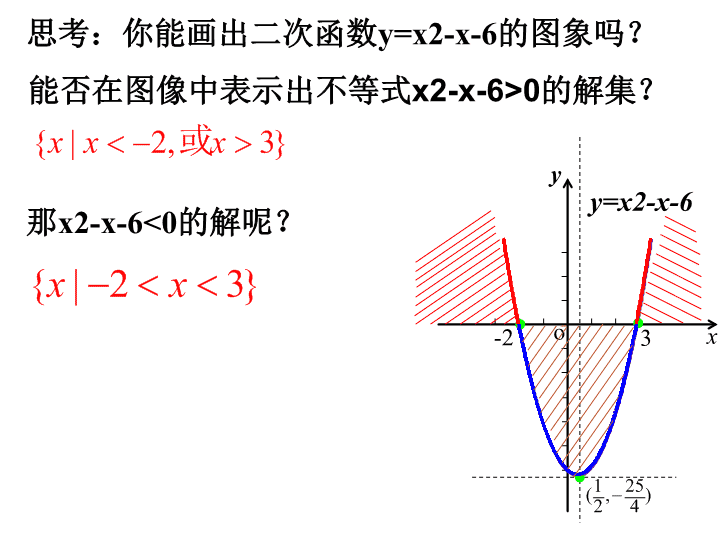
思考:你能画出二次函数y=x2-x-6的图象吗?
y
xo-2 3
1 25( , )2 4
y=x2-x-6
{ | 2, 3}x x x 或
那x2-x-6<0的解呢?
{ | 2 3}x x
能否在图像中表示出不等式x2-x-6>0的解集?
⊿=b2-4ac
二次函数
y=ax2+bx+c(a>0)
的图象
方程
ax2+bx+c=0
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0 (a>0)
的解集
⊿>0 ⊿=0 ⊿<0
有两个不等实
根 x1,x2(x1
x2}
{x|x10.
2
1 2
9 16 25 0
2 3 2 0
1 , 22
x x
x x
解:
解方程 可得
1{ | , 2}.2x x x 原不等式的解集是 或
二、例题讲解
例1:解不等式2x2-3x-2>0.
1{ | , 2}.2x x x 原不等式的解集是 或
2
1 2
2 2 3 2 (2 1)( 2)
(2 1)( 2) 0
1 , 22
x x x x
x x
x x
解 :
由 可解得
二、例题讲解
例2:解不等式4x2-4x+1>0.
2
16 16 0
4 4 1 0
1
2
x x
x
解:
解方程 可得
1{ | }.2x x 原不等式的解集是
二、例题讲解
例2:解不等式4x2-4x+1>0.
2 2
2
2 4 4 1 (2 1)
(2 1) 0
1
2
x x x
x
x
解 :
由 可得
1{ | }.2x x 原不等式的解集是
二、例题讲解
例3:解不等式- x2+2x-3>0.
2 2 3 0x x 解:整理,得
2
4 12 0
2 3 0x x
方程 无实数解
.原不等式的解集是
二、例题讲解
(1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2)判定△与0的关系,并求出方程ax2+bx+c=0 的实根;
(3)写出不等式的解集.
解一元二次不等式的步骤:
练习.解下列不等式:
(1)x2-7x+6≤0;
(2)-2x2+x-5<0;
(3)(x+2)(1-x)<0.
{x|1≤x≤6}
R
(也可先考虑是否能分解因式或配方,不行再判断△)
{x|x<-2,或x>1}
一、基础知识讲解
例4、若不等式x2+px+q<0的解集为{x|10的解集。
解:依题意可知,方程x2+px+q=0的解为x=1或
x=2
即p= -3,q =2
∴x2+qx+p=x2+2x-3
∵方程x2+2x-3=0的解是x= -3或x=1
∴不等式x2+2x-3>0的解集是{x|x<-3,或x>1}
1 2
1 2
p
q
二、例题讲解
解题小结:
若不等式ax2+bx+c>0(a>0)的解集是{x|xx2}
则x1,x2是方程ax2+bx+c=0的两个实根
同理,若不等式ax2+bx+c<0(a>0)的解集是{x|x10 (a>0)
ax2+bx+c<0 (a>0)
(2)求方程ax2+bx+c=0 的实根;
1、解一元二次不等式的步骤:
(3)根据二次函数的图象写出解集
2、分式不等式的解法
例5.解不等式: (x-a)(x+1)<0(a∈R)
解:∵方程(x-a)(x+1)=0的解为
x=a,或x=-1
∴当a>-1时,原不等式的解集为{x|-10
解得 x <-99, 或 x>90
在这个实际问题中x>0,所以这辆汽车刹车前的
车速至少为90km/h.
(1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2)判定△与0的关系,并求出方程ax2+bx+c=0 的实根;
(3)写出不等式的解集.
小结:解一元二次不等式的步骤
求解一元
二次不等式
ax2+bx+c>0
(a>0)的程序
框图:
△≥0
a
bx 2
x< x1或x> x2
某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.
公司A每小时收费1.5元;公司B的收费原则如下:在用户上网的第1小
时内收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若用户
一次上网时间超过17小时,按17小时计算).
一般来说,一次上网时间不会超过17小时,所以,不妨假设一次上网
时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公
司A比选择公司B所需费用少?
解:假设一次上网x小时,则公司A收取的费用为1.5x(元),
公司B收取的费用为1.7x+x(x-1)×(-0.1)/2=x(35-x)/20(元).
如果能够保证选择公司A比选择公司B所需费用少,则
x(35-x)/20 >1.5x (0< x <17).
整理得 x2 - 5x < 0 (0< x <17)
解得 0 < x < 5
所以,当一次上网时间在5小时以内时,选择公司A的费用少;
超过5小时,选择公司B的费用少.
例6 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流
水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系:
y = -2 x2 + 220x.若这家工厂希望在一个星期内利用这条流水线创收
6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?
解:设在一个星期内大约应该生产x辆摩托车
则依题意可得 -2x2 + 220x > 6000
移项整理得 x2 - 110x + 3000 < 0
解得 500.
因为△=81+4×7110>0, 方程x2+9x-7110=0有两个实数根,即
x1≈-88.94, x2≈79.94
画出函数y=x2+9x-7110的图象,由
图象得不等式的解集为
{x|x <-88.94, 或 x>79.94 }
在这个实际问题中,x>0,所以这辆汽车
刹车前的车速至少为79.94km/h.
例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流
水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系:
y = -2 x2 + 220x.若这家工厂希望在一个星期内利用这条流水线创收
6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?
解:设在一个星期内大约应该生产x辆摩托车.
则依题意可得 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为500
解:整理,得 x2 - 2x + 3 < 0
因为△= 4 - 12 = - 8 < 0
方程 2 x2 - 3x – 2 = 0无实数根
例1:解不等式4x2-4x +1>0
解:
由于4x2-4x+1=(2x-1)2>0
所以原不等式的解集为∅