2020高考数学(理)二轮复习题型增分练:2020高考预测卷(二)
2020 高考预测卷(二)
181
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分,考试时间
120 分钟.
第Ⅰ卷
一、选择题:本大题共 12 小题,每个小题 5 分,共 60 分.在每个小题给出
的四个选项中,只有一项是符合题目要求的.
1.已知集合 M={x|x2-4x<0},N={x|m
0,故充分性不成立.若 m·n=|m·n|,
则 m·n=|m|·|n|·cos〈m,n〉=|m|·|n||cos〈m,n〉|,则 cos〈m,n〉=|cos〈m,
n〉|,故 cos〈m,n〉≥0,即 0°≤〈m,n〉≤90°,此时 m 与 n 不一定共线,
即必要性不成立.故“m 与 n 共线”是“m·n=|m·n|”的既不充分也不必要条件,
故选 D.
答案 D
4.甲、乙、丙 3 人参加某项测试,每人通过该测试的概率都为1
3
,测试结束
后,已知甲、乙、丙 3 人中至少有 1 人通过该测试,则甲未通过该测试的概率是
( )
A.1
2 B. 9
20
C.10
19 D. 9
19
解析 设事件 A 为“甲、乙、丙 3 人中至少有 1 人通过该测试”,事件 B
为“甲未通过该测试”.则 P(A)=1- 1-1
3 3=19
27
,P(AB)= 1-1
3 × 1- 1-1
3 2
=10
27
,所以 P(B|A)=PAB
PA
=10
19.
答案 C
5.在△ABC 中,角 A,B 的对边分别为 a,b,若 a=8,b=7,B=60°,则
sinC=( )
A.3 3
14 B.5 3
14
C.3 3
14
或5 3
14 D.11
14
解析 通解 8
sinA
= 7
sin60°
⇒sinA=4 3
7
⇒cosA=±1
7.因为 sinB= 3
2
,cosB=1
2
,
sinC=sin(A+B)=sinAcosB+cosAsinB,所以当 cosA=1
7
时,sinC=5 3
14
;当 cosA
=-1
7
时,sinC=3 3
14 .故 sinC 的值为3 3
14
或5 3
14 .
优解 设角 C 的对边为 c,由余弦定理得,b2=a2+c2-2accosB⇒49=64+
c2-8c⇒c=3 或 c=5.当 c=3 时,sinC=c
b·sinB=3 3
14
;当 c=5 时,sinC=c
b·sinB
=5 3
14 .故 sinC 的值为3 3
14
或5 3
14 .
答案 C
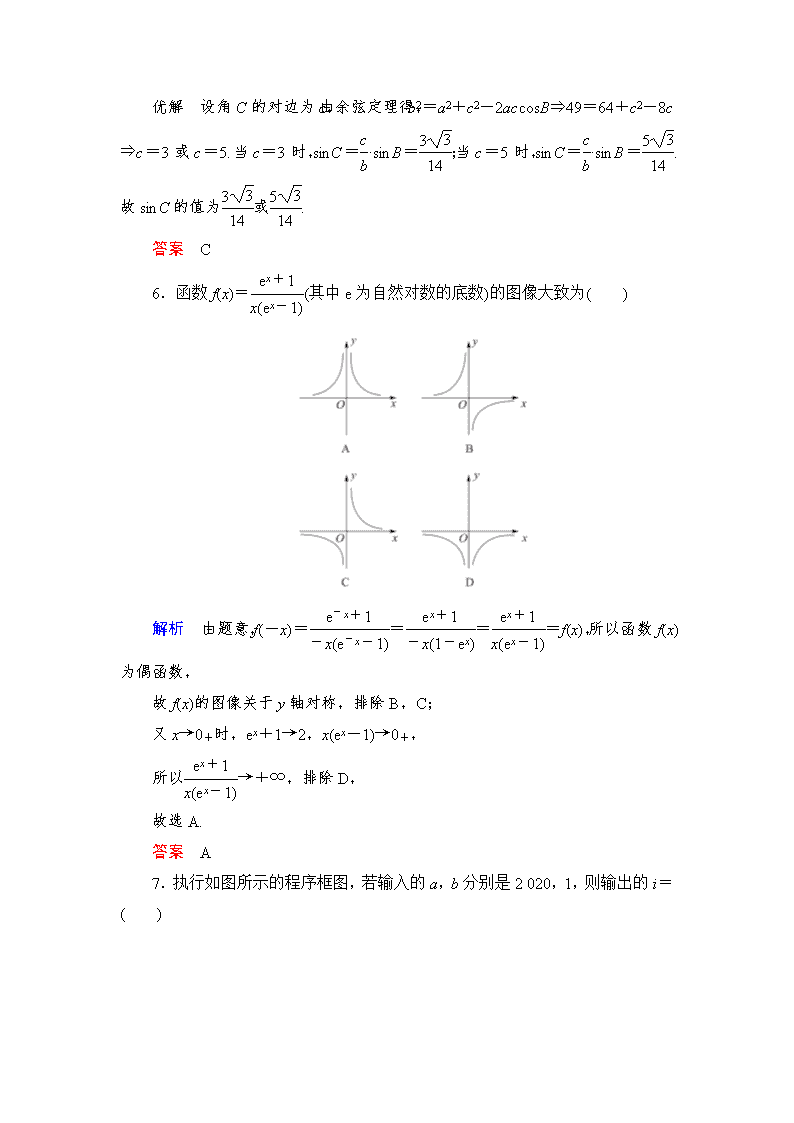
6.函数 f(x)= ex+1
xex-1(其中 e 为自然对数的底数)的图像大致为( )
解析 由题意,f(-x)= e-x+1
-xe-x-1
= ex+1
-x1-ex
= ex+1
xex-1
=f(x),所以函数
f(x)为偶函数,
故 f(x)的图像关于 y 轴对称,排除 B,C;
又 x→0+时,ex+1→2,x(ex-1)→0+,
所以 ex+1
xex-1
→+∞,排除 D,
故选 A.
答案 A
7.执行如图所示的程序框图,若输入的 a,b 分别是 2 020,1,则输出的 i
=( )
A.5 B.6
C.7 D.8
解析 i=1,a=2 020+1,b=1=1!;
i=2,a=2 020+3,b=2×1=2!;
…
i=n,a=2 020+nn+1
2
,b=n!.
当 i=6 时,a=2 020+21=2 041,b=6!=720a.
故输出的 i 的值为 7.
答案 C
8.我国南北朝时的数学著作《张邱建算经》有一道题为:“今有十等人,
每等一人,官赐金依等次差降之.上三人先入,得金四斤,持出.下三人后入,
得金三斤,持出.中间四人未到者,亦依等次更给.问各得金几何?”在该问题
中,等级较高的二等人所得黄金比等级较低的九等人所得黄金( )
A.多 1 斤 B.少 1 斤
C.多1
3
斤 D.少1
3
斤
解析 等级由高到低的十等人所得黄金由多到少依次记为 a1,a2,…,a10,
则 a1,a2,…,a10 成等差数列.由题意得 a1+a2+a3=3a2=4,a2=4
3
,a8+a9+
a10=3a9=3,a9=1.则 a2-a9=4
3
-1=1
3
,即等级较高的二等人所得黄金比等级较
低的九等人所得黄金多1
3
斤.
答案 C
9.把正方形 ABCD 沿对角线 AC 折起,当以 A,B,C,D 四点为顶点棱锥
体积最大时,直线 BD 和平面 ABC 所成角的大小为( )
A.90° B.60°
C.45° D.30°
解析 如图,当 DO⊥平面 ABC 时,三棱锥 DABC 的体积最大.
∴∠DBO 为直线 BD 和平面 ABC 所成的角,
∵在 Rt△DOB 中,OD=OB,
∴直线 BD 和平面 ABC 所成角的大小为 45°.
答案 C
10.在区间[0,1]上随机取两个数 x,y,记 p1 为事件“x+y≥1
2
”的概率,p2
为事件“|x-y|≤1
2
”的概率,p3 为事件“xy≤1
2
”的概率,则( )
A.p10,|φ|<π
2 ,f(α)=-1,f(β)=1,若|α
-β|的最小值为3π
4
,且 f(x)的图像关于点
π
4
,1 对称,则函数 f(x)的单调递增区间
是( )
A.
-π
2
+2kπ,π+2kπ ,k∈Z
B.
-π
2
+3kπ,π+3kπ ,k∈Z
C. π+2kπ,5π
2
+2kπ ,k∈Z
D. π+3kπ,5π
2
+3kπ ,k∈Z
解析 由题设条件可知 f(x)的周期 T=4|α-β|min=3π,所以ω=2π
T
=2
3
,又 f(x)
的图像关于点
π
4
,1 对称,从而 f
π
4 =1,即 sin
2
3
×π
4
+φ =0.
因为|φ|<π
2
,所以φ=-π
6
,故 f(x)=2sin
2
3x-π
6 +1,再由-π
2
+2kπ≤2
3x-π
6
≤π
2
+2kπ,k∈Z,得-π
2
+3kπ≤x≤π+3kπ,k∈Z.
答案 B
12.已知函数 f(x)是奇函数,且 f(x)+f′(x)=ln(x+1)-ln(1-x)+ 2
1-x2
,则
|f(2x-1)|<|f x+1
2 |的解集是( )
A.
1
6
,1
3 B.
1
6
,1
4
C.
1
3
,1
2 D.
1
6
,1
2
解析 ∵f(x)是奇函数,∴f(-x)=-f(x),两边同时求导数得,-f′(-x)=
-f′(x),则 f′(-x)=f′(x),即 f′(x)为偶函数.
∴f(-x)+f′(-x)=ln(-x+1)-ln(1+x)+ 2
1-x2
,
则-f(x)+f′(x)=ln(-x+1)-ln(1+x)+ 2
1-x2
,
与 f(x)+f′(x)=ln(x+1)-ln(1-x)+ 2
1-x2
联立可得
fx=ln1+x-ln1-x,
f′x= 2
1-x2.
又 f(x)的定义域为(-1,1),∴f′(x)= 2
1-x2>0,
∴f(x)在(-1,1)上为单调递增函数.
∴在(0,1)上,f(x)>f(0)=0,∴|f(x)|为偶函数,且在(0,1)上单调递增.
∴由|f(2x-1)|<|f x+1
2 |,
可得
-1<2x-1<1,
-10,b>0)上一点 C,过双曲线中心的直线交双曲
线于 A,B 两点,记直线 AC,BC 的斜率分别为 k1,k2,当 2
k1k2
+ln|k1|+ln|k2|最小
时,双曲线的离心率为________.
解析 设 A(x1,y1),C(x2,y2),
由题意知,点 A,B 为过原点的直线与双曲线x2
a2
-y2
b2
=1 的交点,∴由双曲
线的对称性,得 A,B 关于原点对称,∴B(-x1,-y1),
∴k1k2=y2-y1
x2-x1
·y2+y1
x2+x1
=y22-y21
x22-x21
,
∵点 A,C 都在双曲线上,∴x21
a2
-y21
b2
=1,x22
a2
-y22
b2
=1,
两式相减,可得 k1k2=b2
a2>0,
对于 2
k1k2
+ln|k1|+ln|k2|= 2
k1k2
+ln|k1k2|,
设函数 y=2
x
+ln x,x>0,
由 y′=-2
x2
+1
x
=0,得 x=2,
当 x>2 时,y′>0,当 00 取得最小值,
∴当 2
k1k2
+ln(k1k2)最小时,k1k2=b2
a2
=2,
∴e= 1+b2
a2
= 3.
答案 3
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~
21 题为必考题,每个试题考生都必须作答.第 22、23 题为选考题,考生根据要
求作答.
(一)必考题:共 60 分
17.(12 分)平面四边形 ABCD 中,AB⊥BC,∠A=60°,AB=3,AD=2.
(1)求 sin∠ABD;
(2)若 cos∠BDC=1
7
,求△BCD 的面积.
解析 (1)在△ABD 中,∠A=60°,AB=3,AD=2,
由余弦定理,得 BD2=AB2+AD2-2AB·AD·cosA=9+4-6=7,所以 BD=
7,(2 分)
由正弦定理,得 BD
sinA
= AD
sin∠ABD
,(4 分)
所以 sin∠ABD=AD·sinA
BD
=
2× 3
2
7
= 3
7
= 21
7 .(6 分)
(2)因为 AB⊥BC,所以∠ABC=90°,
所以 cos∠DBC=sin∠ABD= 3
7
,
所以 sin∠DBC= 2
7 .
因为 cos∠BDC=1
7
,所以 sin∠BDC=4 3
7 .(8 分)
所以 sinC=sin(π-∠BDC-∠DBC)
=sin(∠BDC+∠DBC)
=sin∠BDCcos∠DBC+cos∠BDCsin∠DBC
=4 3
7
× 3
7
+1
7
× 2
7
= 2
7.(10 分)
所以 sin∠DBC=sinC,所以∠DBC=∠C,
所以 DC=BD= 7,所以 S△BCD=1
2DC·BD·sin∠BDC=1
2
× 7× 7×4 3
7
=
2 3.(12 分)
18.(12 分)某省级示范高中高三年级对考试的评价指标中,有“难度系数”
和“区分度”两个指标.其中,难度系数=年级总平均分
总分
,
区分度=实验班的平均分-普通班的平均分
总分 .
(1)在某次数学考试(满分 150 分)中,从实验班和普通班各随机抽取三人,实
验班三人的成绩分别为 147 分,142 分,137 分,普通班三人的成绩分别为 97
分,102 分,113 分,通过样本估算本次考试的区分度(精确到 0.01).
(2)以下表格是高三年级 6 次考试的统计数据:
难度系数 x 0.64 0.71 0.74 0.76 0.77 0.82
区分度 y 0.18 0.23 0.24 0.24 0.22 0.15
①计算相关系数 r,|r|<0.75 时,认为相关性弱;|r|≥0.75 时,认为相关性强.通
过计算说明,能否利用线性回归模型拟合 y 与 x 的关系;
②已知 t=|x-0.74|,求出 y 关于 t 的线性回归方程,并预报 x=0.75 时 y 的
值(精确到 0.01).
参考数据:错误!iyi=0.9309,错误!≈0.0112,错误!iyi=0.0483,错误!(ti-
t→)2≈0.0073.
参考公式:相关系数 r=错误!=错误!,线性回归方程中斜率和截距的最小二
乘估计公式分别为b^=错误!=错误!,a^= y→-b^ x→.
解析 (1)易求得实验班三人成绩的平均分为147+142+137
3
=142(分),
普通班三人成绩的平均分为97+102+113
3
=104(分),
所以区分度为142-104
150
≈0.25.(3 分)
(2)①由表格数据知,
x→=0.64+0.71+0.74+0.76+0.77+0.82
6
=0.74,
y→=0.18+0.23+0.24+0.24+0.22+0.15
6
=0.21,
r=错误!≈
0.9309-6×0.74×0.21
0.0112
≈-0.13,
故|r|<0.75,相关性较弱.(6 分)
综上可知,不能利用线性回归模型拟合 y 与 x 的关系.(7 分)
②y 与 t 的值如下表:
t 0.10 0.03 0 0.02 0.03 0.08
区分度 y 0.18 0.23 0.24 0.24 0.22 0.15
则b^=错误!≈
0.0483-6×0.26
6 ×0.21
0.0073
≈-0.86,
a^=y^-b^ t→=0.21+0.86×0.26
6 ≈0.25.
故所求回归方程为 y=-0.86t+0.25,(11 分)
当 x=0.75 时,t=0.01,所以 y≈0.24.(12 分)
19.(12 分)在四棱锥 PABCD 中,AB∥CD,CD=2AB.
(1)设 AC 与 BD 相交于点 M,AN→=mAP→(m>0),且 MN∥平面 PCD,求实数
m 的值;
(2)若 AB=AD=DP,∠BAD=60°,PB= 2AD,且 PD⊥AD,求二面角 BPCD
的正弦值.
解析 因为 AB∥CD,
所以AM
MC
=AB
CD
=1
2
,即AM
AC
=1
3.(1 分)
因为 MN∥平面 PCD,MN⊂平面 PAC,平面 PAC∩平面 PCD=PC,
所以 MN∥PC.(2 分)
所以AN
AP
=AM
AC
=1
3
,即 m=1
3.(3 分)
(2)因为 AB=AD,∠BAD=60°,可知△ABD 为等边三角形,
所以 BD=AD=PD,又 BP= 2AD,
故 BP2=PD2+DB2,所以 PD⊥DB.
由已知 PD⊥AD,AD∩BD=D,
所以 PD⊥平面 ABCD.(5 分)
如图,以 D 为坐标原点,DA→ ,DP→ 的方向为 x,y 轴的正方向建立空间直角坐
标系,
设 AB=1,则 AB=AD=DP=1,CD=2,
所以 B
1
2
,0, 3
2 ,P(0,1,0),C(-1,0, 3)
则PB→=
1
2
,-1, 3
2 ,PC→=(-1,-1, 3),(6 分)
设平面 PBC 的一个法向量 m=(x1,y1,z1),则有
m·PB→=0,
m·PC→=0,
即 x1-2y1+ 3z1=0,
x1+y1- 3z1=0.
设 x1=1,则 y1=2,z1= 3,
所以 m=(1,2, 3),(8 分)
设平面 PCD 的一个法向量为 n=(x2,y2,z2),
由已知可得
n·DC→ =0,
n·DP→ =0,
即 x2- 3z2=0,
y2=0.
令 z2=1,则 x2= 3,所以 n=( 3,0,1).(10 分)
所以 cos〈m,n〉= m·n
|m|·|n|
= 6
4 .
设二面角 BPCD 的平面角为θ,则 sinθ= 10
4 .(12 分)
20.(12 分)已知抛物线 C:y=-x2,点 A,B 在抛物线上,且横坐标分别为
-1
2
,3
2
,抛物线 C 上的点 P 在 A,B 之间(不包括点 A,点 B),过点 B 作直线 AP
的垂线,垂足为 Q.
(1)求直线 AP 的斜率 k 的取值范围;
(2)求|PA|·|PQ|的最大值.
解析 (1)由题意可知 A
-1
2
,-1
4 ,B
3
2
,-9
4 ,
设 P(xP,-x2P),-1
20,
当-1
20 时,证明:不等式 f(x)≤m
x
在 0,1+1
m 上恒成立.
解析 (1)由题意得 f′(x)=-[mx-(m+1)](x-1)·e-x,(1 分)
①当 m=0 时,则 f′(x)=(x-1)e-x,
令 f′(x)>0 时,则 x>1;令 f′(x)<0,则 x<1.
∴f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.(2 分)
②当 m<0 时,令 f′(x)<0,则 1+1
m0,则 x<1+1
m
或 x>1.
∴f(x)在 -∞,1+1
m 和(1,+∞)上单调递增,在 1+1
m
,1 上单调递减.(3
分)
③当 m>0 时,令 f′(x)<0,则 x<1 或 x>1+1
m
;
令 f′(x)>0,则 10 时,f(x)在(0,1]上单调递减,在 1,1+1
m 上单调递增,
当 x∈(0,1]时,f(x)=mx2-x+m
ex 1,
则 g′(x)=ex-(2x+1),
令 h(x)=ex-(2x+1),x>1,则 h′(x)=ex-2>0,
∴h(x)=g′(x)在(1,+∞)上单调递增,且 g′(1)=e-3<0,
g′
3
2 =e3
2
-4>0,
∴存在 x0∈ 1,3
2 ,使得 g′(x0)=0,即 ex0-(2x0+1)=0,
∴当 x∈(1,x0)时,g′(x)<0,当 x∈ x0,3
2 时,g′(x)>0,
∴g(x)在(1,x0)上单调递减,在 x0,3
2 上单调递增,
∴g(x)min=g(x0)=ex0-x20-x0=-x20+x0+1=- x0-1
2 2+5
4>0,
当 x>1 时,g(x)=ex-x(x+1)>0,
即 ex>x(x+1),
∴e1+1
m
≥ 1+1
m 2+1
m ,
∴不等式 f(x)≤m
x
在 0,1+1
m 上恒成立.(12 分)
(二)选考题:共 10 分.请考生在第 22、23 题中任选一题作答,如果多做,
则按所做的第一题计分.
22.(10 分)选修 4-4:坐标系与参数方程
已知直线l经过点P(1,2),倾斜角α=π
6
,圆C的极坐标方程为ρ=2 2cos θ-π
4 .
(1)写出直线 l 的参数方程的标准形式,并把圆 C 的方程化为直角坐标方程;
(2)若直线 l 与圆 C 相交于 A,B 两点,求线段 AB 的中点 M 到点 P 的距离.
解析 (1)直线 l 的参数方程为
x=1+tcosπ
6
,
y=2+tsinπ
6
,
即
x=1+ 3
2 t,
y=2+t
2
(t 为参数,t∈R).
由ρ=2 2cos θ-π
4 ,
得ρ=2cosθ+2sinθ,
∴ρ2=2ρcosθ+2ρsinθ,
∴x2+y2=2x+2y,
∴圆 C 的直角坐标方程为(x-1)2+(y-1)2=2.(5 分)
(2)把
x=1+ 3
2 t,
y=2+t
2
代入(x-1)2+(y-1)2=2 得,
1+ 3
2 t-1 2+ 2+t
2
-1 2=2,
整理得 t2+t-1=0,
Δ=5>0,t1+t2=-1,
∴|MP|=|t1+t2
2 |=1
2.(10 分)
23.(10 分)选修 4-5:不等式选讲
已知函数 f(x)=x2-|x|+3.
(1)求不等式 f(x)≥3x 的解集;
(2)若关于 x 的不等式 f(x)-x2≤|x
2
+a|恒成立,求实数 a 的取值范围.
解析 (1)当 x≥0 时,f(x)=x2-x+3≥3x,
即 x2-4x+3≥0,
解得 x≥3 或 x≤1,所以 x≥3 或 0≤x≤1;
当 x<0 时,f(x)=x2+x+3≥3x,
此不等式 x2-2x+3≥0 恒成立,所以 x<0.
综上所述,原不等式的解集为{x|x≥3 或 x≤1}.(5 分)
(2)f(x)-x2≤|x
2
+a|恒成立,
即-|x|+3≤|x
2
+a|恒成立,
即|x
2
+a|+|x|≥3 恒成立,
∵|x
2
+a|+|x|=|x
2
+a|+|x
2|+|x
2|
≥|x
2
+a-x
2|+|x
2|=|a|+|x
2|≥|a|,
当且仅当 x=0 时,等号成立,
∴|a|≥3,解得 a≥3 或 a≤-3.
故实数 a 的取值范围是(-∞,-3]∪[3,+∞).(10 分)