2013年数学高考江西卷（文）

2013年数学高考江西卷（文）

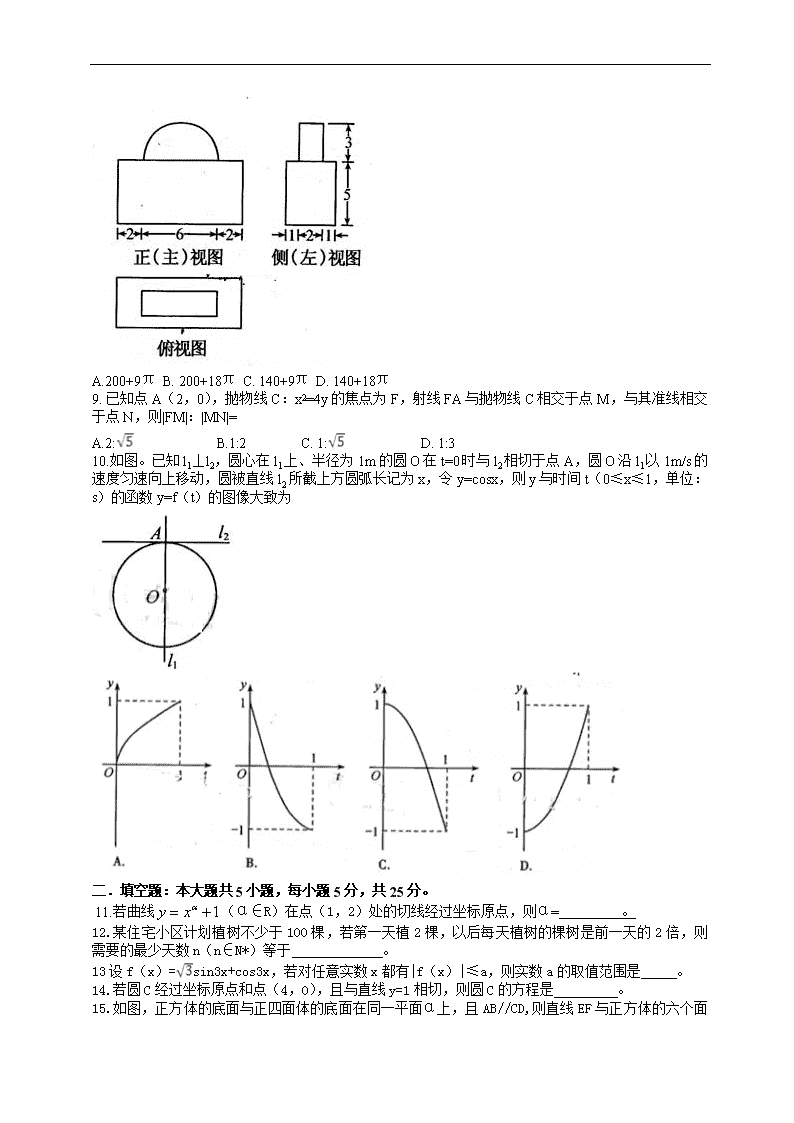
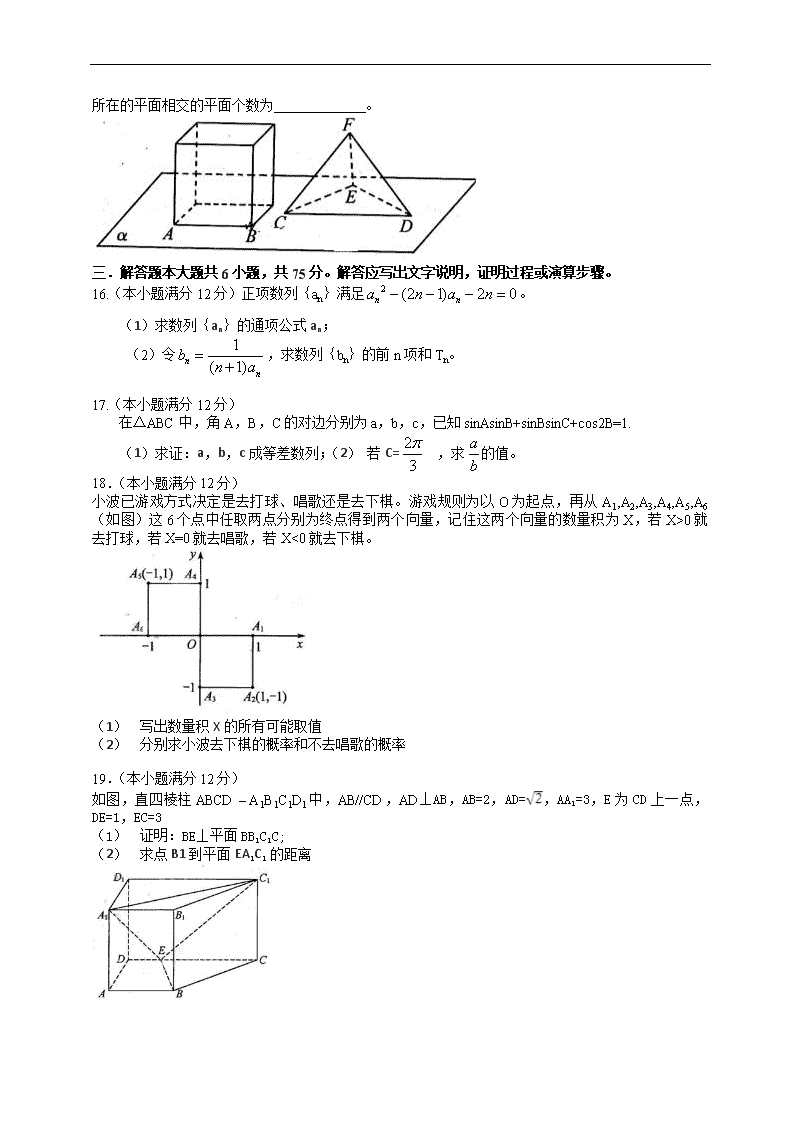
‎2013年普通高等学校招生全国统一考试（江西卷）‎ 文科数学 第Ⅰ卷 一. 选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.复数z=i（-2-i）（i为虚数单位）在复平面内所对应的点在 A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎2.若集合A=｛x∈R|ax2+ax+1＝0｝其中只有一个元素，则a=‎ A.4 B‎.2 C.0 D.0或4‎ ‎3. （ ）‎ A. B. C. D. ‎4.集合A={2,3},B={1,2,3},从A,B中各取任意一个数，则这两数之和等于4的概率是 A． B. C. D. ‎5.总体编号为01，02，…19，20的20个个体组成。利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为 A.08 B‎.07 C.02 D.01‎ ‎6. 下列选项中，使不等式x＜＜成立的x的取值范围是（ ）‎ A.（，-1） B. （-1，0） C.0，1） D.（1，+）‎ ‎7.阅读如下程序框图，如果输出i=4，那么空白的判断框中应填入的条件是 A.S＜8 B. S＜‎9 ‎‎ C. S＜10 D. S＜11‎ ‎8.一几何体的三视图如右所示，则该几何体的体积为 A.200+9π B. 200+18π C. 140+9π D. 140+18π ‎ ‎9. 已知点A（2，0），抛物线C：x2=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|=‎ A.2: B.1:‎2 C. 1: D. 1:3‎ ‎10.如图。已知l1⊥l2，圆心在l1上、半径为‎1m的圆O在t=0时与l2相切于点A，圆O沿l1以‎1m/s的速度匀速向上移动，圆被直线l2所截上方圆弧长记为x，令y=cosx，则y与时间t（0≤x≤1，单位：s）的函数y=f（t）的图像大致为 二．填空题：本大题共5小题，每小题5分，共25分。‎ ‎ 11.若曲线（α∈R）在点（1，2）处的切线经过坐标原点，则α= 。‎ ‎12.某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵树是前一天的2倍，则需要的最少天数n（n∈N*）等于 。‎ ‎13设f（x）=sin3x+cos3x，若对任意实数x都有|f（x）|≤a，则实数a的取值范围是 。 ‎ ‎14.若圆C经过坐标原点和点（4，0），且与直线y=1相切，则圆C的方程是 。‎ ‎15.如图，正方体的底面与正四面体的底面在同一平面α 上，且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为 。‎ 三．解答题本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。‎ ‎16.（本小题满分12分）正项数列｛an｝满足。‎ ‎（1）求数列｛an｝的通项公式an；‎ ‎（2）令，求数列｛bn｝的前n项和Tn。‎ ‎17.（本小题满分12分）‎ 在△ABC中，角A，B，C的对边分别为a，b，c，已知sinAsinB+sinBsinC+cos2B=1.‎ ‎（1）求证：a，b，c成等差数列；（2） 若C=，求的值。‎ ‎18．（本小题满分12分）‎ 小波已游戏方式决定是去打球、唱歌还是去下棋。游戏规则为以O为起点，再从A1,A2,A3,A4,A5,A6（如图）这6个点中任取两点分别为终点得到两个向量，记住这两个向量的数量积为X，若X>0就去打球，若X=0就去唱歌，若X<0就去下棋。‎ （1） 写出数量积X的所有可能取值 （2） 分别求小波去下棋的概率和不去唱歌的概率 ‎19．（本小题满分12分）‎ 如图，直四棱柱ABCD – A1B‎1C1D1中，AB//CD，AD⊥AB，AB=2，AD=，AA1=3，E为CD上一点，DE=1，EC=3‎ （1） 证明：BE⊥平面BB‎1C1C;‎ （2） 求点B1 到平面EA‎1C1 的距离 ‎20.（本小题满分13分）‎ 椭圆C:=1(a>b>0)的离心率，a+b=3‎ (1) 求椭圆C的方程；‎ (2) 如图，A,B,D是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线DP交x轴于点N直线AD交BP于点M，设BP的斜率为k，MN的斜率为m，证明‎2m-k为定值。‎ ‎21．（本小题满分14分）‎ 设函数 a 为 常数且a∈（0，1）.‎ （1） 当a=时，求f（f（））； ‎ （2） 若x0满足f（f（x0））= x0,但f（x0）≠x0，则称x0为f（x）的二阶周期点，证明函数有且仅有两个二阶周期点，并求二阶周期点x1，x2；‎ （3） 对于（2）中x1，x2，设A（x1,f（f（x1））），B（x2,f（f（x2）））,C(a2,0)，记△ABC的面积为s（a），求s（a）在区间[,]上的最大值和最小值。‎ 参考答案 一、选择题 ‎1．D ‎ ‎2．A ‎ ‎3．C ‎ ‎4．C ‎ ‎5．D ‎ ‎6．A ‎ ‎7．B ‎ ‎8．A ‎ ‎9．C ‎ ‎10．B ‎ ‎11．2 ‎ ‎12．6 ‎ ‎13． ‎ ‎14． ‎ ‎15．4 ‎ ‎16．解：‎ 由于｛an｝是正项数列，则。‎ ‎（2）由（1）知，故 ‎17．解：（1）由已知得sinAsinB+sinBsinC+1-2sin2B=1.故sinAsinB+sinBsinC=2sin2B 因为sinB不为0，所以sinA+sinC=2sinB再由正弦定理得a+c=2b,所以a，b，c成等差数列 ‎（2）由余弦定理知得化简得 ‎18．解：（1） x 的所有可能取值为-2 ，-1 ，0， 1。‎ ‎（2）数量积为-2的只有一种 数量积为-1的有，六种 数量积为0的有四种 数量积为1的有四种 故所有可能的情况共有15种。‎ 所以小波去下棋的概率为 因为去唱歌的概率为，所以小波不去唱歌的概率 ‎19．解.（1）证明：过B作CD的垂线交CD于F，则 在 在，故 由 ‎（2）‎ ‎，‎ 同理，‎ 因此。设点B1到平面的距离为d，则 ‎，从而 ‎20．解： 所以再由a+b=3得a=2,b=1,‎ ‎ ①‎ 将①代入，解得 又直线AD的方程为 ②‎ ①与②联立解得 由三点共线可角得 所以MN的分斜率为m=，则（定值）‎ ‎21．解：（1）当时，‎ ‎（‎ 当时，由解得x=0,由于f（0）=0,故x=0不是f（x）的二阶周期点；‎ 当时由解得 因 故是f（x）的二阶周期点；‎ 当时，由解得 因故不是f（x）的二阶周期点；‎ 当时，解得 ‎ 因 故是f（x）的二阶周期点。‎ 因此，函数有且仅有两个二阶周期点，，。‎ ‎（3）由（2）得 ‎ 则 因为a在[,]内，故，则 故 ‎ ‎