2021版高考数学一轮复习核心素养测评五十七双曲线理北师大版

2021版高考数学一轮复习核心素养测评五十七双曲线理北师大版

核心素养测评五十七 双曲线 ‎ ‎(30分钟　55分)‎ 一、选择题(每小题5分,共35分)‎ ‎1.(2020·合肥模拟)已知双曲线的一条渐近线方程为y=2x,且经过点,则该双曲线的标准方程为 (　　)‎ A.-y2=1　　　　　 B.-x2=1‎ C.x2-=1 D.y2-=1‎ ‎【解析】选B.对于A选项,双曲线的渐近线方程为y=±x,不符合题意.对于B选项,双曲线的渐近线方程为y=±2x,且过点,符合题意.对于C选项,双曲线的渐近线为y=±2x,但不过点,不符合题意.对于D选项,双曲线的渐近线为y=±x,不符合题意.‎ ‎2.(2019·全国卷Ⅲ)双曲线C:-=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,若=,则△PFO的面积为 (　　)‎ A.　　B.　　C.2　　D.3‎ ‎【解析】选A.由双曲线的方程-=1可得一条渐近线方程为y=x;‎ 在△PFO中,|PO|=|PF|,过点P作PH⊥OF,垂足为H,‎ 因为tan∠POF=得到PH=;‎ 所以S△PFO=××=.‎ - 14 -‎ ‎3.已知曲线-=1(a>0,b>0)为等轴双曲线,且焦点到渐近线的距离为,则该双曲线的方程为 (　　)‎ A.x2-y2= B.x2-y2=1‎ C.x2-y2= D.x2-y2=2‎ ‎【解析】选D.由已知,若曲线-=1(a>0,b>0)为等轴双曲线,则a2=b2,‎ c==a,即焦点的坐标为(±a,0);‎ 渐近线方程为x±y=0,‎ 若焦点到渐近线的距离为,则=a=,双曲线的标准方程为-=1,即x2-y2=2.‎ ‎4.(2018·全国卷I)已知双曲线C:-y2=1,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M,N.若△OMN为直角三角形,则= (　　)‎ A. 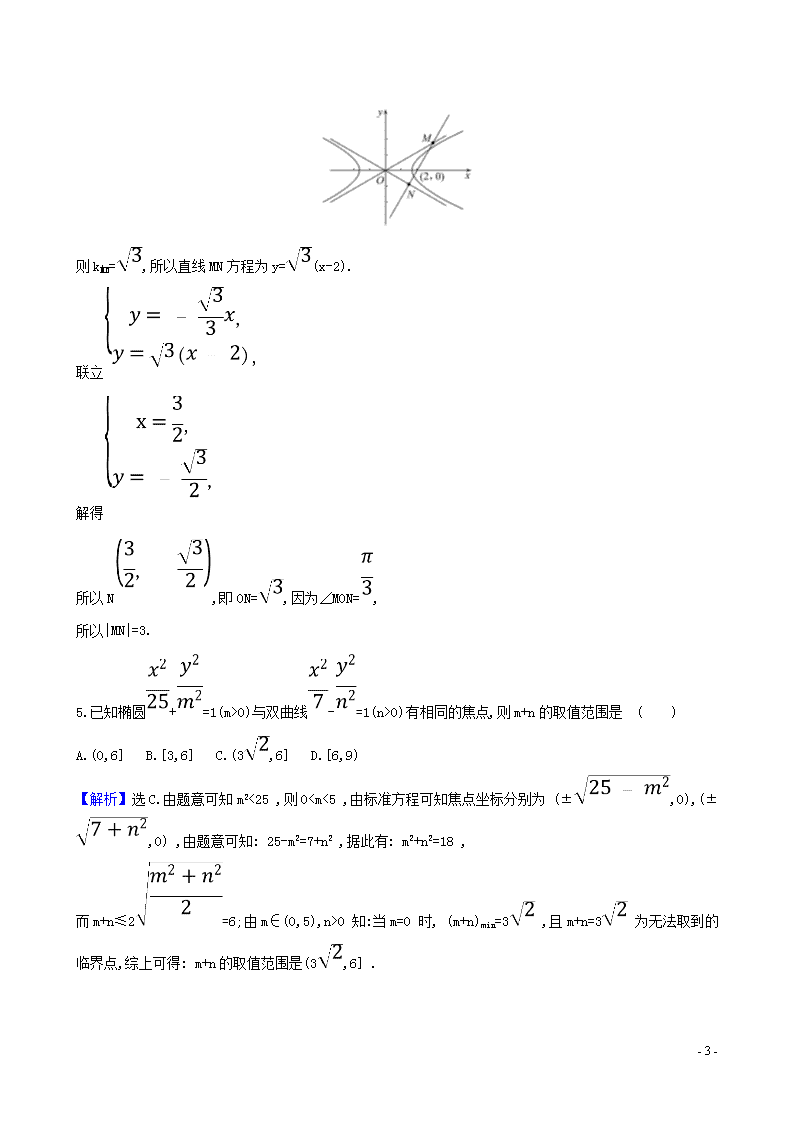B.3 C.2 D.4‎ ‎【解析】选B.渐近线方程为-y2=0,即y=±x,‎ 所以∠MON=.‎ 因为△OMN为直角三角形,假设∠ONM=,如图,‎ - 14 -‎ 则kMN=,所以直线MN方程为y=(x-2).‎ 联立 解得 所以N,即ON=,因为∠MON=,‎ 所以|MN|=3.‎ ‎5.已知椭圆+=1(m>0)与双曲线-=1(n>0)有相同的焦点,则m+n的取值范围是 (　　)‎ A.(0,6]　 B.[3,6]　 C.(3,6]　 D.[6,9)‎ ‎【解析】选C.由题意可知m2<25 ,则00 知:当m=0 时, (m+n)min=3 ,且m+n=3 为无法取到的临界点,综上可得: m+n的取值范围是(3,6] .‎ - 14 -‎ ‎6.已知F1,F2分别为双曲线C: -=1的左、右焦点, P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为 (　　)‎ A.　 B.　 C.　 D.‎ ‎【解析】选D.双曲线C:-=1的两个焦点F1(-3,0),F2(3,0),|F1F2|=6,a=2,由|PF1|=2|PF2|,‎ 设|PF2|=x,则|PF1|=2x,由双曲线的性质知,2x-x=4,解得x=4,所以|PF1|=8,|PF2|=4,‎ 因为|F1F2|=6,所以cos∠F1PF2==,所以sin∠F1PF2=,所以△PF1F2外接圆的半径为=,所以△PF1F2外接圆的面积为.‎ ‎7.(2020·杭州模拟)已知椭圆C1:+=1(a>b>0)与双曲线C2:-=1(m>0,n>0)有相同的焦点F1,F2,点P是两曲线的一个公共点,且∠F1PF2=60°,若椭圆e1=,则双曲线C2的离心率e2= (　　)‎ A.　 B.　 C.3　 D.4‎ ‎【解析】选B.设|PF1|=s,|PF2|=t,P为第一象限的交点,由椭圆和双曲线的定义可得s+t=2a,s-t=2m,解得s=a+m,t=a-m,在△F1PF2中,∠F1PF2=60°,可得4c2=s2+t2-2stcos 60°=a2+m2+2am+a2+m2-2am-(a2-m2),即有a2+3m2=4c2,可得+=4,即+=4,由e1=,可得e2=.‎ 二、填空题(每小题5分,共10分)‎ ‎8.双曲线+=1的焦距为________________. ‎ - 14 -‎ ‎【解析】由题意可得(25-k)(9-k)<0,解得90,9-k<0,双曲线方程为-=1,‎ 由c2=a2+b2=(25-k)+(k-9)=16,即c=4,所以2c=8.‎ 答案:8‎ ‎9.(2020·安庆模拟)已知双曲线-=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为________________. ‎ ‎【解析】因为渐近线方程为y=x,所以=,抛物线y2=24x的准线方程为x=-6,因此双曲线的一个焦点为(-6,0),其半焦距c=6,由双曲线的性质c2=a2+b2,‎ 所以a2=9,b2=27,‎ 故方程为-=1.‎ 答案:-=1‎ 三、解答题 ‎10.(10分)已知双曲线-=1,过点M(m,0)作垂直于双曲线实轴的直线与双曲线交于A,B两点.若△AOB是锐角三角形(O为坐标原点),求实数m的取值范围. ‎ ‎【解析】由题意得A,‎ Bm,-2,‎ - 14 -‎ 所以=,=,因为△AOB是锐角三角形,所以∠AOB是锐角,即与的夹角为锐角,所以·>0,即m2-+4>0,解得-2,故实数m的取值范围是(-2,-)∪(,2).‎ ‎(15分钟　35分)‎ ‎1.(5分)已知双曲线-=1(b>0),以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD 的面积为2b,则双曲线的方程为 (　　)‎ A.-=1 B.-=1‎ C.-=1 D.-=1‎ ‎【解析】选D.不妨设A(x0,y0)在第一象限,‎ 由已知 由①③得=,④‎ 所以=×=,⑤‎ 由②④⑤得b2=12.‎ - 14 -‎ 所以双曲线的方程为-=1.‎ ‎【变式备选】‎ 已知动圆M与圆C1:(x+4)2+y2=2 外切,与圆C2:(x-4)2+y2=2内切,则动圆圆心M的轨迹方程为 (　　)‎ A.-=1(x≥)‎ B.-=1(x≤-)‎ C.+=1(x≥)‎ D.+=1(x≤-)‎ ‎【解析】选A.设动圆的半径为r,由题意可得|MC1|=r+,|MC2|=r-,所以|MC1|-|MC2|=2=2a,故由双曲线的定义可知动点M在以C1(-4,0),C2(4,0)为焦点,实轴长为2a=2的双曲线的右支上,即a=,c=4⇒b2=16-2=14,故其标准方程为-=1(x≥).‎ ‎2.(5分)过双曲线-=1(a>0,b>0)的右焦点且垂直于x轴的直线与双曲线交于A,B两点,与双曲线的两条渐近线交于C,D两点,若|AB|≥|CD|,则双曲线离心率的取值范围为 (　　)‎ A.　 B.‎ - 14 -‎ C. D.‎ ‎【解析】选B.将x=c代入-=1,得y=±,‎ 不妨取A,B,则|AB|=,将x=c代入y=±x,得y=±,不妨取C,D,则|CD|=.因为|AB|≥|CD|,所以≥×,即b≥c,则b2≥c2,又c2-a2=b2,‎ 所以c2-a2≥c2,即c2≥a2,则e2≥,则e≥.‎ ‎【变式备选】‎ ‎(2020·武汉模拟)已知A,B,C是双曲线-=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且2|AF|=|CF|,则该双曲线的离心率是 (　　)‎ A.　　 B.　　 C.　 　D.‎ ‎【解析】选B.设左焦点为F′,|AF|=m,连接AF′,CF′,则|FC|=2m,|AF′|=2a+m,|CF′|=2a+2m,|FF′|=2c,‎ 因为BF⊥AC,且AB经过原点O,‎ 所以四边形FAF′B为矩形,‎ 在Rt△AF′C中,|AF′|2+|AC|2=|F′C|2,代入(2a+m)2+(3m)2=(2a+2m)2,‎ - 14 -‎ 化简得m=,所以在Rt△AF′F中,|AF′|2+|AF|2=|F′F|2,‎ 代入+=(2c)2,‎ 化简得= ,即e=.‎ ‎3.(5分)P是双曲线C:x2-y2=2左支上一点,直线l是双曲线C的一条渐近线,P在l上的射影为Q,F2是双曲线C的右焦点,则|PF2|+|PQ|的最小值为 (　　)‎ A.　 B.　 C.3　 D.2+‎ ‎【解析】选C.由题知|PF2|-|PF1|=2a=2,则|PF2|+|PQ|=|PF1|+|PQ|+2,由对称性,当F1,P,Q在同一直线上时|PF1|+|PQ|最小,由渐近线方程y=x,|F1O|=2知|F1Q|=,则|PF2|+|PQ|的最小值为3.‎ ‎4.(10分)(2019·福州模拟)已知双曲线C的焦点在坐标轴上,其渐近线方程为y=±x,过点P. ‎ ‎(1)求双曲线C的标准方程.‎ ‎(2)是否存在被点B(1,1)平分的弦?如果存在,求出弦所在的直线l的方程;如果不存在,请说明理由.‎ ‎【解析】(1)双曲线C的焦点在坐标轴上,其渐近线方程为y=±x,‎ 设双曲线方程为x2-=λ(λ≠0),‎ - 14 -‎ 过点P,代入可得λ=1,‎ 所求双曲线方程为x2-=1.‎ ‎(2)假设直线l存在.设B(1,1)是弦MN的中点,‎ 且M(x1,y1),N(x2,y2),则x1+x2=2,y1+y2=2.因为M,N在双曲线上,所以 所以2(x1+x2)(x1-x2)-(y1-y2)(y1+y2)=0,‎ 所以4(x1-x2)=2(y1-y2),所以k==2,‎ 所以直线l的方程为y-1=2(x-1),即2x-y-1=0,‎ 联立方程组 ,得2x2-4x+3=0,‎ 因为Δ=16-4×3×2=-8<0,‎ 所以直线l与双曲线无交点,所以直线l不存在.‎ ‎ 5.(10分)已知离心率为的椭圆的中心在原点,焦点在x轴上,双曲线以椭圆的长轴为实轴,短轴为虚轴,且焦距为2. ‎ ‎(1)求椭圆及双曲线的方程.‎ ‎(2)设椭圆的左、右顶点分别为A,B,在第二象限内取双曲线上一点P,连接BP交椭圆于点M,连接PA并延长交椭圆于点N,若=,求四边形ANBM的面积.‎ ‎【解析】(1)设椭圆方程为+=1(a>b>0),则根据题意知双曲线的方程为-=1且满足解方程组得 - 14 -‎ 所以椭圆的方程为+=1,双曲线的方程为-=1.‎ ‎(2)由(1)得A(-5,0),B(5,0),|AB|=10,‎ 设M(x0,y0),则由=得M为BP的中点,所以P点坐标为(2x0-5,2y0).‎ 将M,P坐标代入椭圆和双曲线方程,‎ 得 消去y0,得2-5x0-25=0.‎ 解之,得x0=-或x0=5(舍去).‎ 所以y0=.‎ 由此可得M,所以P(-10,3).‎ 当P为(-10,3)时,‎ 直线PA的方程是y=(x+5),‎ 即y=-(x+5),代入+=1,‎ 得2x2+15x+25=0.‎ 所以x=-或-5(舍去),‎ 所以xN=-,xN=xM,MN⊥x轴.‎ - 14 -‎ 所以S四边形ANBM=2S△AMB=2××10×=15.‎ ‎1.(2020·上饶模拟)过双曲线-=1(a>0,b>0)的左焦点F1,作圆x2+y2=a2的切线交双曲线的右支于点P,切点为T,PF1的中点M在第一象限,则以下结论正确的是 (　　)‎ A.b-a=|MO|-|MT| ‎ B.b-a>|MO|-|MT|‎ C.b-a<|MO|-|MT|‎ D.b-a=|MO|+|MT|‎ ‎【解析】选A.如图,连接OT,PF2,则OT⊥F1T,在直角三角形OTF1中,‎ ‎|F1T|==b,‎ 因为M为线段F1P的中点,O为F1F2的中点,‎ 所以|OM|=|PF2|,‎ 所以|MO|-|MT|=|PF2|-|PF1|-|F1T|‎ ‎=(|PF2|-|PF1|)+b=×(-2a)+b=b-a.‎ - 14 -‎ ‎2.(2019·赣州模拟)双曲线-=1(a>0,b>0)的左、右焦点为F1,F2,渐近线分别为l1,l2,过点F1且与l1垂直的直线分别交l1及l2于P,Q两点,若满足=+,则双曲线的离心率为 (　　)‎ A.　　　B.　　　C.2　　　D.‎ ‎【解析】选C.因为-=1(a>0,b>0)的左、右焦点为F1,F2,‎ 所以F1(-c,0),F2(c,0),‎ 双曲线的两条渐近线方程为y=-x,y=x,‎ 因为过F1的直线分别交双曲线的两条渐近线于点P,Q.‎ 又因为=+,‎ 所以点P是线段F1Q的中点,且PF1⊥OP,‎ 所以过F1的直线PQ的斜率kPQ=,‎ 所以过F1的直线PQ的方程为y=(x+c),‎ 解方程组,得P,‎ 所以|PF1|=|PQ|=b,|PO|=a,|OF1|=|OF2|=‎ ‎|OQ|=c,|QF2|=2a,‎ 因为tan∠QOF2=,所以cos ∠QOF2=,‎ 由余弦定理,得 - 14 -‎ cos ∠QOF2==1-=,‎ 即e2-e-2=0,‎ 解得e=2或e=-1(舍).‎ - 14 -‎