数学理卷·2018届广东省广雅学校高三上学期第一次月考（2017

数学理卷·2018届广东省广雅学校高三上学期第一次月考（2017

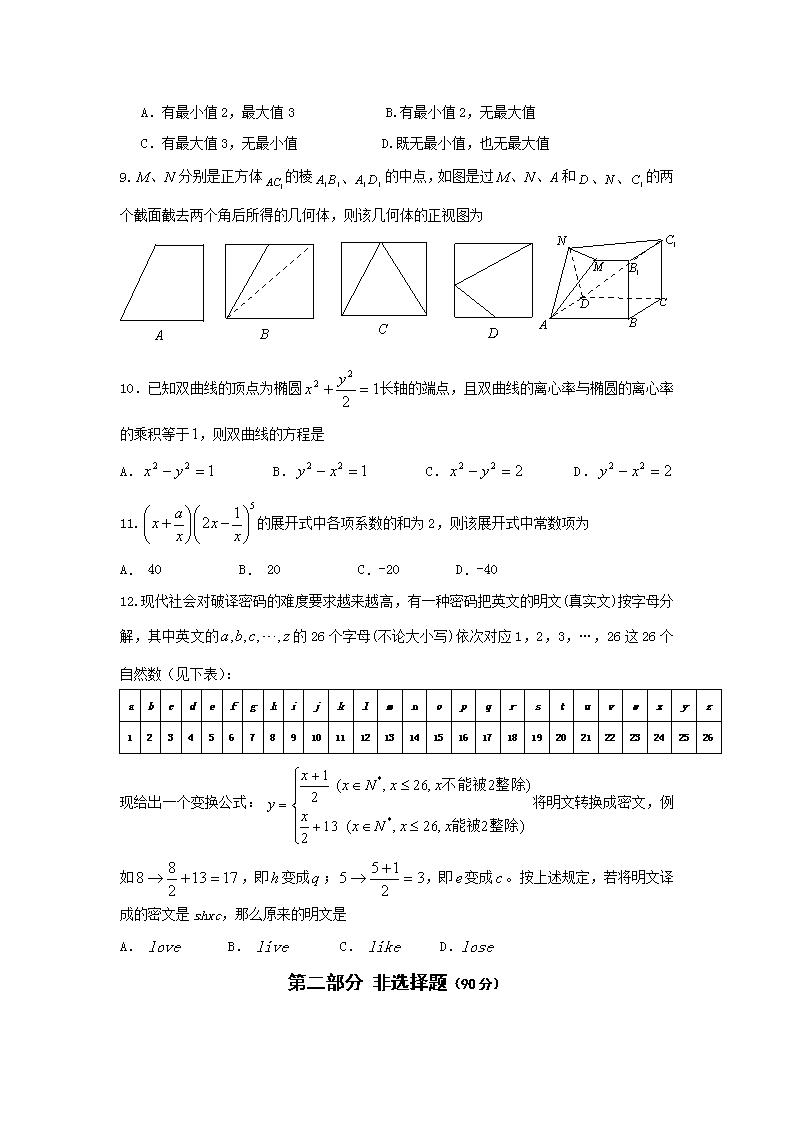
阳东广雅中学2018届高三第一次月考 理科数学 试题 本试卷分选择题和非选择题两部分，共4页，满分150分，考试用时120分钟。‎ 第一部分 选择题（共60分）‎ 一、选择题(每题5分，共60分)‎ ‎1. 已知集合，，则 ‎ A. B. C. D. ‎ ‎2.命题“，”的否定为 ‎ A．， B． ‎ C．, D．,‎ ‎3. 复数（）在复平面上所对应的点在第二象限上，则的取值范围是 ‎ A. B. C. D. ‎ ‎4.已知，则的最小值是 A．2 B． C．4 D．5‎ ‎5. 从数字，，，，中任取个，组成一个没有重复数字的两位数，则这个两位数大于的概率是 A． B． C． D． ‎ ‎6．设、是两个命题，若是真命题，那么 ‎ A．是真命题且是假命题 B．是真命题且是真命题 　 ‎ C．是假命题且是真命题 D．是假命题且是假命题 ‎ ‎7.若是常数, 则“且”是“对任意,有”的 ‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎8.设满足则 A．有最小值2，最大值3 B.有最小值2，无最大值 C．有最大值3，无最小值 D.既无最小值，也无最大值 ‎9. 分别是正方体的棱的中点，如图是过和的两个截面截去两个角后所得的几何体，则该几何体的正视图为 ‎ ‎10．已知双曲线的顶点为椭圆长轴的端点，且双曲线的离心率与椭圆的离心率的乘积等于，则双曲线的方程是 A． B． 　 C． D．‎ ‎11.的展开式中各项系数的和为2，则该展开式中常数项为 A． 40 B． 20 C．-20 D．-40‎ ‎12.现代社会对破译密码的难度要求越来越高，有一种密码把英文的明文(真实文)按字母分解，其中英文的的26个字母(不论大小写)依次对应1，2，3，…，26这26个自然数（见下表）：‎ a b c d e f g h i j k l m n o p q r s t u v w x y z ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ 现给出一个变换公式：将明文转换成密文，例如，即变成；，即变成。按上述规定，若将明文译成的密文是shxc，那么原来的明文是 ‎ A． love B． live C． like D．lose 第二部分 非选择题（90分）‎ 二、填空题(每题5分，共20分)‎ ‎13.已知函数，若，则的值为 ‎ ‎14. ‎ ‎15. 若，则__________． ‎ ‎16.某学校开设A类选修课3门，B类选修课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有 种.(用数字作答) ‎ 三、计算题(第17~21题每题12分，22题10分，共70分)‎ ‎17．(本小题满分12分)已知 ‎（1）若是的充分条件，求实数的取值范围；‎ ‎（2）若为真命题，为假命题，求实数的取值范围.‎ ‎18.（本小题满分12分） 某公司有一批专业技术人员，对他们进行年龄状况和接受教育程度(学历)的调查，其结果(人数分布)如下表：‎ 学历 ‎35岁以下 ‎35～50岁 ‎50岁以上 本科 ‎80‎ ‎30‎ ‎20‎ 研究生 ‎20‎ ‎（1）用分层抽样的方法在35～50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率；‎ ‎（2）在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取个人，其中35岁以下48人，50岁以上10人，再从这个人中随机抽取出1人，此人的年龄为50岁以上的概率为，求、的值.‎ ‎19．(本小题满分12分)在等比数列中，，公比，且 ‎，又与的等比中项为。‎ ‎（1）求数列的通项公式；‎ ‎（2）设，数列的前项和为，求数列的通项公式。并求当最大时的值. ‎ ‎20.（本小题满分12分）近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病，为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查，得到如下的列联表。‎ ‎ ‎ 已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为，‎ ‎ （1）请将上面的列联表补充完整；‎ ‎ （2）是否有的把握认为患心肺疾病与性别有关？说明你的理由；‎ ‎ （3）已知在患心肺疾病的10位女性中，有3位又患有胃病，现在从患心肺疾病的10位女性中，选出3名进行其它方面的排查，记选出患胃病的女性人数为，求的分布列、数学期望以及方差。‎ ‎ 下面的临界值表仅供参考：‎ ‎ ‎ ‎21. （本小题满分12分）已知函数，，‎ ‎（1）若，试确定函数的单调区间；‎ ‎（2）若，且对于任意的，恒成立，试确定实数的取值范围；‎ ‎（3）设函数，求证：，‎ ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系中，过点的直线的倾斜角为．以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为,直线和曲线的交点为点．‎ ‎（1）求直线的参数方程； （2）求的值．‎ 阳东广雅中学2018届高三第一次月考 理科数学答案 一、选择题(每题5分，共60分)‎ CCBCC DBBBD AA 二、填空题(每题5分，共20分)‎ ‎13. —1或9 14. 15. 16. 30‎ 三、计算题(第17~21题每题12分，22题10分，共70分)‎ ‎17．解：‎ ‎（1）∵p是q的充分条件，‎ ‎∴[﹣2，6] [2﹣m，2+m]‎ ‎∴∴实数m的取值范围是[4，+∞）．﹣﹣﹣（6分）‎ ‎（2）当m=5时，q：﹣3≤x≤7．据题意有，p与q一真一假．﹣（7分）‎ p真q假时，由﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）‎ p假q真时，由．﹣﹣（11分）‎ ‎∴实数x的取值范围为[﹣3，﹣2）∪（6，7]．﹣﹣﹣﹣﹣（12分）‎ ‎18．（1） 解: 用分层抽样的方法在35～50岁中抽取一个容量为5的样本, 设抽取学历为本科的人数为，‎ ‎ ∴ , 解得. …… 2分 ‎ ∴ 抽取了学历为研究生2人，学历为本科3人，分别记作S1、S2 ；B1、B2、B3 .‎ 从中任取2人的所有基本事件共10个: (S1, B1),(S1, B2),(S1, B3),(S2, B1),(S2, B2), ‎ ‎(S2, B3), (S1, S2), (B1, B2), (B2, B3), (B1, B3). ‎ 其中至少有1人的学历为研究生的基本事件有7个: (S1, B1),(S1, B2),(S1, B3),(S2, B1), ‎ ‎(S2, B2), (S2, B3), (S1, S2). …… 4分 ‎∴ 从中任取2人，至少有1人的教育程度为研究生的概率为. …… 6分 ‎（2）解: 依题意得： ，解得. …… 8分 ‎ ∴ 35～50岁中被抽取的人数为.‎ ‎ ∴. …… 10分 ‎ 解得. ∴. …… 12分 ‎19．解：（1），，‎ 又 ‎ 又与的等比中项为， ‎ 而， ‎ ‎， … … … …5分 ‎（2） ‎ 是以为首项，为公差的等差数列 ‎ ‎ … … … …9分 ‎ ‎ 当时，；当时，；当时，‎ 当或时，最大. … … … …12分 ‎20. （1）列联表补充如下： ‎ ‎ ---2分 ‎（2）解：因为，‎ ‎ 即，又，‎ ‎ 那么，我们有99.5%的把握认为患心肺疾病与性别有关。 ---6分 ‎（3）的所有可能取值为0，1，2，3. ‎ ‎； ；‎ ‎ ； ‎ 分布列如下：‎ ‎ ----10分 ‎ 则，‎ ‎ 。‎ ‎ 的数学期望与方差分别为，。 ----12分 ‎21. 解：（1）由得：，所以，由，得，故的单调增区间为，单调减区间为。 ----2分 ‎ （2）由可知为偶函数，于是对任意的成立，等价于对任意的成立，由，得，----3分 ‎①当时，，此时在上为增函数；故 ‎，符合题意； ---------5分 ‎②当时，，当变化时，、的变化情况如下表：‎ ‎ ‎ 由此可得，在上，，依题意，，‎ 又，，， 综合①②得：实数的取值范围是。‎ ‎ ----8分 ‎（3），‎ ‎（10分）‎ ‎，，，，‎ 由此得：‎ ‎ ‎ 故 。 ---12分 ‎22.解：（1）由条件知，直线的倾斜角，.‎ 设点是直线上的任意一点，点到点的有向距离为，则 ‎………5分 ‎（2）曲线的直角坐标方程为,由此得,‎ 即 . ‎ ‎………10分 设为此方程的两个根，因为和的交点为，所以分别是点 所对应的参数，由韦达定理得 =.‎