高考数学一轮复习第一章集合与常用逻辑用语1-1集合练习理北师大版

高考数学一轮复习第一章集合与常用逻辑用语1-1集合练习理北师大版

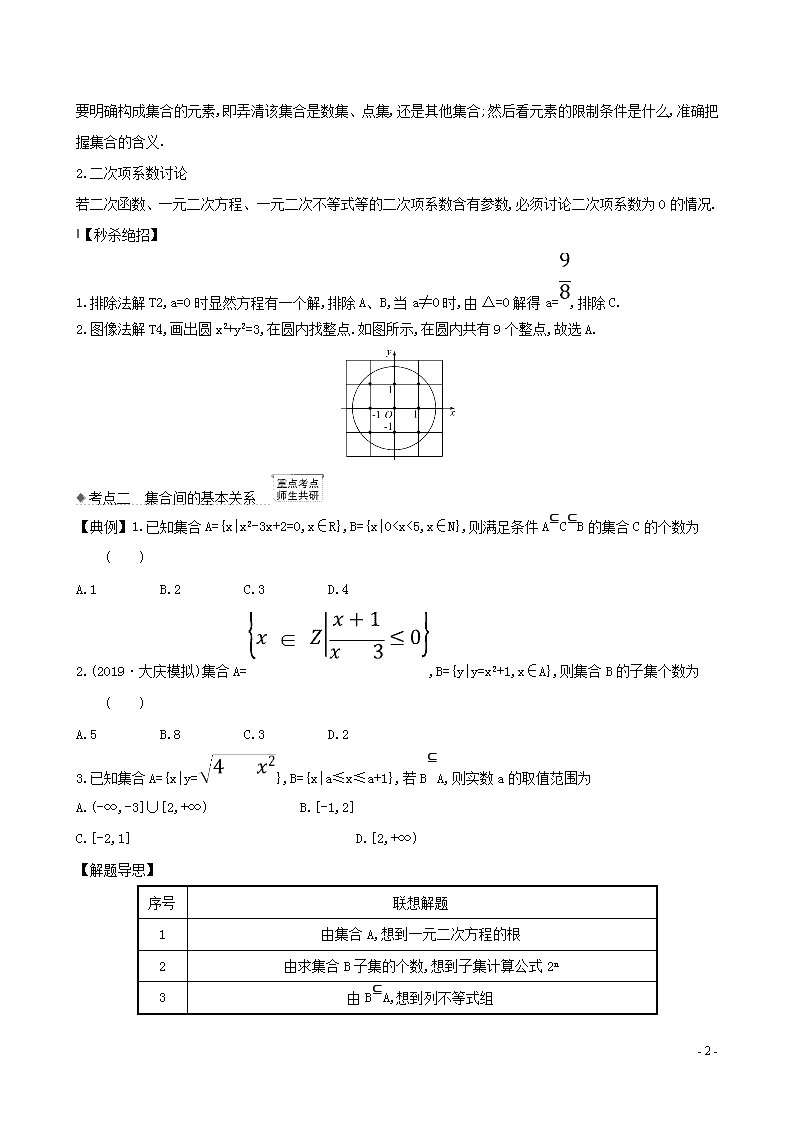
‎1.1 集合 核心考点·精准研析 考点一　集合的基本概念 ‎ ‎1.已知集合A={1,2,4},则集合B={(x,y)|x∈A,y∈A}中元素的个数为 (　　)‎ A.3 B.6 C.8 D.9‎ ‎2.若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a= (　　)‎ A. B. C.0 D.0或 ‎3.已知a,b∈R,若={a2,a+b,0},则a2 021+b2 021为 (　　)‎ A.1 B.0 C.-1 D.±1‎ ‎4.(2018·全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为 (　　)‎ A.9 B.8 C.5 D.4‎ ‎【解析】1.选D.集合B中元素有(1,1),(1,2),(1,4),(2,1),(2,2),‎ ‎(2,4),(4,1),(4,2),(4,4),共9个.‎ ‎2.选D.若集合A中只有一个元素,则方程ax2-3x+2=0只有一个实根或有两个相等实根.‎ 当a=0时,x=,符合题意;‎ 当a≠0时,由Δ=(-3)2-8a=0得a=,所以a的取值为0或.‎ ‎3.选C.由已知得a≠0,则=0,所以b=0,于是a2=1,即a=1或a=-1,又根据集合中元素的互异性可知a=1应舍去,因此a=-1,故a2 021+b2 021=(-1)2 021+02 021=-1.‎ ‎4.选A.由x2+y2≤3知,-≤x≤,-≤y≤.又x∈Z,y∈Z,所以x∈{-1,0,1},y∈{-1,0,1},所以A中元素的个数为9.‎ ‎1.集合定义应用 - 6 -‎ 要明确构成集合的元素,即弄清该集合是数集、点集,还是其他集合;然后看元素的限制条件是什么,准确把握集合的含义.‎ ‎2.二次项系数讨论 若二次函数、一元二次方程、一元二次不等式等的二次项系数含有参数,必须讨论二次项系数为0的情况.‎ ‎【秒杀绝招】‎ ‎1.排除法解T2,a=0时显然方程有一个解,排除A、B,当a≠0时,由Δ=0解得a=,排除C.‎ ‎2.图像法解T4,画出圆x2+y2=3,在圆内找整点.如图所示,在圆内共有9个整点,故选A.‎ 考点二　集合间的基本关系 ‎ ‎【典例】1.已知集合A={x|x2-3x+2=0,x∈R},B={x|00},则RA= (　　)‎ A.{x|-12}‎ D.{x|x≤-1}∪{x|x≥2}‎ ‎2.(2019·资阳模拟)设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为 (　　)‎ A.{x|x≤-1或x≥3} B.{x|x<1或x≥3}‎ C.{x|x≤1} D.{x|x≤-1}‎ - 6 -‎ ‎【解析】1.选B.方法一:A={x|(x-2)(x+1)>0}={x|x<-1或x>2},所以RA={x|-1≤x≤2}.‎ 方法二:因为A={x|x2-x-2>0},所以RA={x|x2-x-2≤0}={x|-1≤x≤2}.‎ ‎2.选D.图中阴影部分表示集合为U(A∪B),又A={x|-1-1},所以U(A∪B)={x|x≤-1}.‎ 怎样求阴影部分所表示的集合?‎ 提示:先用集合间的关系和集合的运算表示阴影,再根据集合运算求解.‎ 利用集合的运算求参数 ‎【典例】1.集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为 (　　)‎ A.0 B.1 C.2 D.4‎ ‎2.已知集合A={x|a-12‎ C.a≥-1 D.a>-1‎ ‎【解析】选D.由A∩B≠∅知,集合A,B有公共元素,作出数轴,如图所示:‎ 易知a>-1.‎ 已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为 ‎(　　)‎ A.77 B.49 C.45 D.30‎ ‎【解析】选C.集合A表示如图所示的所有“