- 2021-07-01 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北省石家庄二中2020届高三6月高考全仿真测试文科数学试题
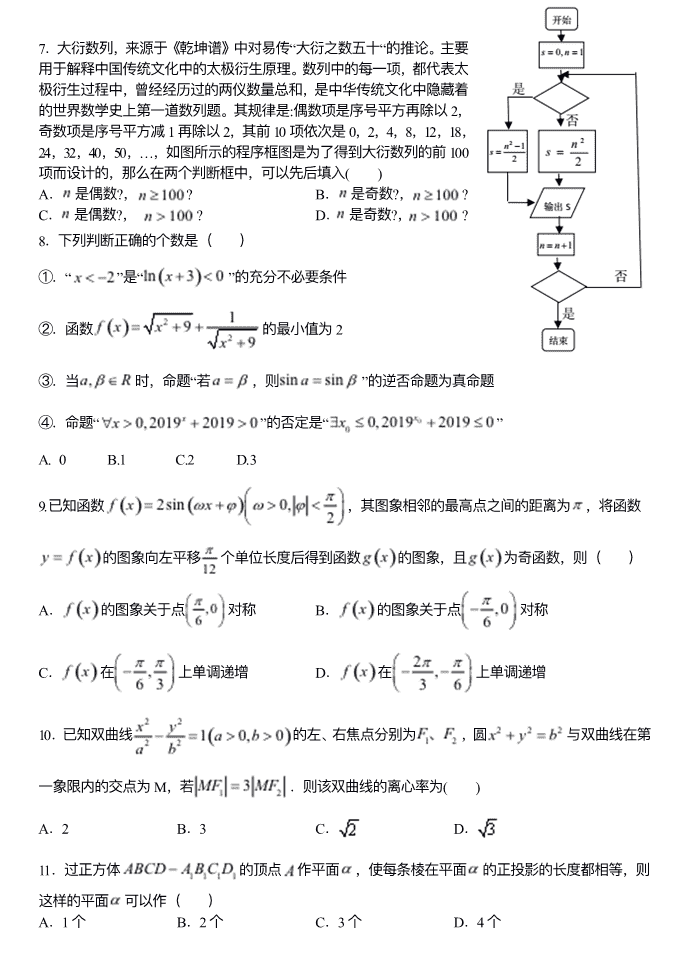
2020 年普通⾼等学校招⽣全国统⼀考试 ⽂科数学(模拟) 注意事项: 1.答卷前,考⽣务必将⾃⼰的姓名、考⽣号等填写在答题卡和试卷指定位置上。 2.回答选择题时,选出每⼩题答案后,⽤铅笔把答题卡对应题⽬的答案标号涂⿊。如需改动,⽤ 橡⽪擦⼲净后,再选涂其它答案标号。回答⾮选择题时,将答案写在答题卡上。写在本试卷上⽆效。 3.考试结束后,将本试卷和答题卡⼀并交回。 ⼀、选择题(本题共 12 ⼩题,每⼩题 5 分,共 60 分。在每⼩题给出的四个选项中,只有⼀项是符合 题⽬要求的。) 1.设集合 , ,则 ( ) A. B. C. D. 2.满⾜条件 的复数 对应点的轨迹是( ) A.直线 B.圆 C.椭圆 D.双曲线 3.已知 ,令 , , ,那么 之间的⼤⼩关系为( ) A. B. C. D. 4.若 tan(α+β)=3,tanβ=2,则 =( ) A. B.7 C.﹣ D.﹣7 5.某学⽣ 5 次考试的成绩(单位:分)分别为 85,67,m,80,93,其中 m>0,若该学⽣在这 5 次考 试中成绩的中位数为 80,则得分的平均数不可能为( ) A.70 B.75 C.80 D.85 6..已知函数 f(x)的部分图象如图所示,则 f(x)可能的解析式是 ( ) A.f(x)=sinx• B.f(x)=cosx• C.f(x)=﹣sinx• D.f(x)=﹣cosx• 7.⼤衍数列,来源于《乾坤谱》中对易传“⼤衍之数五⼗“的推论。主要 ⽤于解释中国传统⽂化中的太极衍⽣原理。数列中的每⼀项,都代表太 极衍⽣过程中,曾经经历过的两仪数量总和,是中华传统⽂化中隐藏着 的世界数学史上第⼀道数列题。其规律是:偶数项是序号平⽅再除以 2, 奇数项是序号平⽅减 1 再除以 2,其前 10 项依次是 0,2,4,8,12,18, 24,32,40,50,…,如图所示的程序框图是为了得到⼤衍数列的前 100 项⽽设计的,那么在两个判断框中,可以先后填⼊( ) A. 是偶数?, ? B. 是奇数?, ? C. 是偶数?, ? D. 是奇数?, ? 8.下列判断正确的个数是( ) ①.“ ”是“ ”的充分不必要条件 ②.函数 的最⼩值为 2 ③.当 时,命题“若 ,则 ”的逆否命题为真命题 ④.命题“ ”的否定是“ ” A. 0 B.1 C.2 D.3 9.已知函数 ,其图象相邻的最⾼点之间的距离为 ,将函数 的图象向左平移 个单位⻓度后得到函数 的图象,且 为奇函数,则( ) A. 的图象关于点 对称 B. 的图象关于点 对称 C. 在 上单调递增 D. 在 上单调递增 10.已知双曲线 的左、右焦点分别为 ,圆 与双曲线在第 ⼀象限内的交点为 M,若 .则该双曲线的离⼼率为( ) A.2 B.3 C. D. 11.过正⽅体 的顶点 作平⾯ ,使每条棱在平⾯ 的正投影的⻓度都相等,则 这样的平⾯ 可以作( ) A.1 个 B.2 个 C.3 个 D.4 个 12.已知 ,若 有四个不同的实根 ,且 ,则 的取值范围( ) A. B. C. D. ⼆.填空题(本题共 4 ⼩题,每⼩题 5 分,共 20 分) 13.曲线 在(0,0)处的切线⽅程为 14.已知平⾯向量 满⾜ , , ,则 与 的夹⻆为________. 15.设数列 的前 项和为 ,若 且当 时, ,则 的通项公式 _______. 16.四棱锥 中,底⾯ 是边⻓为 的正⽅形,侧⾯ 是以 为斜边的等腰直⻆三⻆ 形,若 ,则四棱锥 的体积取值范围为_____. 三.解答题(共 70 分。解答应写出⽂字说明、证明过程或演算步骤。第 17~21 题为必考题,每个 试题考⽣都必须作答。第 22、23 题为选考题,考⽣根据要求作答) (⼀)必考题:60 分。 17.(12 分)△ 的内⻆ 所对的边分别为 ,已知 . (Ⅰ )求 ; (Ⅱ )若 ,且△ 的⾯积为 ,求 . 18.(12 分)四棱锥 S﹣ABCD 如图所示,其中四边形 ABCD 是 直⻆梯形,AB⊥ AD,AD⊥ DC,SA⊥ 平⾯ ABCD,DA=DC= AB,AC 与 BD 交于点 G,直线 SC 与平⾯ ABCD 所成⻆的余弦值为 ,点 M 线段 SA 上. (1)若直线 SC∥ 平⾯ MBD,求 的值; (2)若 DA=1,求点 A 到平⾯ SCD 的距离. 19.(12 分)2019 年 12 ⽉以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病 例,均诊断为病毒性肺炎肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID ﹣19),简称“新冠肺炎”,下图是 2020 年 1 ⽉ 15 ⽇⾄ 1 ⽉ 24 ⽇累计确诊⼈数随时间变化的散点图. 为了预测在未采取强⼒措施下,后期的累计确诊⼈数,建⽴了累计确诊⼈数 y 与时间变量 t 的两个 回归模型,根据 1 ⽉ 15 ⽇⾄ 1 ⽉ 24 ⽇的数据(时间变量 t 的值依次 1,2,…,10)建⽴模型 和 . 参考数据:其中 , . 1.511 1.512 1.513 1.514 1.515 5.5 390 17 385 6000 31500 134720 87 130 195 290 440 (1)根据散点图判断, 和 哪⼀个适宜作为累计确诊⼈数 y 与时间变量 t 的 回归⽅程类型?(给出判断即可,不必说明理由); (2)根据(1)的判断结果及附表中数据,建⽴ y 关于 t 的回归⽅程; (3)以下是 1 ⽉ 25 ⽇⾄ 1 ⽉ 29 ⽇累计确诊⼈数的真实数据,根据(2)的结果回答下列问题: 时间 1 ⽉ 25 ⽇ 1 ⽉ 26 ⽇ 1 ⽉ 27 ⽇ 1 ⽉ 28 ⽇ 1 ⽉ 29 ⽇ 累计确诊⼈数的真实数 据 1975 2744 4515 5974 7111 (i)当 1 ⽉ 25 ⽇⾄ 1 ⽉ 27 ⽇这 3 天的误差(模型预测数据与真实数据差值的绝对值与真实数据的 ⽐值)都⼩于 0.1 则认为模型可靠,请判断(2)的回归⽅程是否可靠? (ii)2020 年 1 ⽉ 24 ⽇在⼈⺠政府的强⼒领导下,全国⼈⺠共同采取了强⼒的预防“新冠肺炎”的措 施,若采取措施 5 天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否 有效?并说明理由. 附:对于⼀组数据(u1,v1),(u2,v2),……,(un,vn),其回归直线 的斜率和截距的最 ⼩⼆乘估计分别为: , . 20.(12 分)已知椭圆 的离⼼率为 ,其右顶点为 ,下顶点为 ,定点 , 的⾯积为 ,过点 作与 轴不重合的直线 交椭圆 于 两点,直线 分别与 轴交于 两点. (1)求椭圆 的⽅程; (2)试探究 的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由. (⼆)选考题:共 10 分。请考⽣在第 22、23 题中任选⼀题作答,如果多做,则按所做的第⼀题计分。 22[选修 4–4:坐标系与参数⽅程](10 分) 在平⾯直⻆坐标系 中,已知曲线 的参数⽅程为 ( 为参数),直线 的参数⽅程为 ( 为参数),点 的坐标为 . (1)若点 在曲线 上运动,点 在线段 上运动,且 ,求动点 的轨迹⽅程. (2)设直线 与曲线 交于 两点,求 的值. 23.[选修 4–5:不等式选讲](10 分) (1)已知 ,且 ,证明: ; (2)已知 ,且 ,证明: .查看更多