- 2021-07-01 发布 |
- 37.5 KB |
- 25页

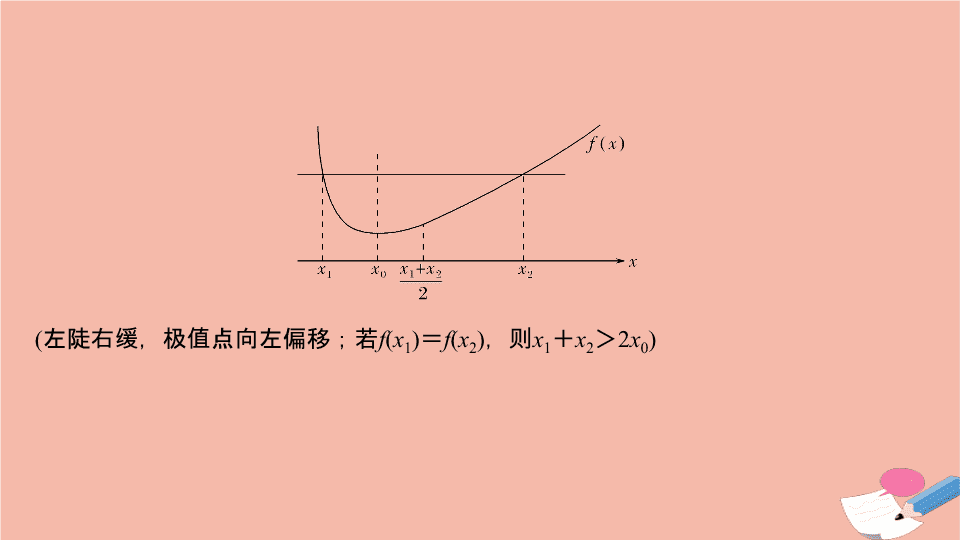
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省2021届高考数学一轮复习第四章导数及其应用补上一课极值点的“偏移”问题课件
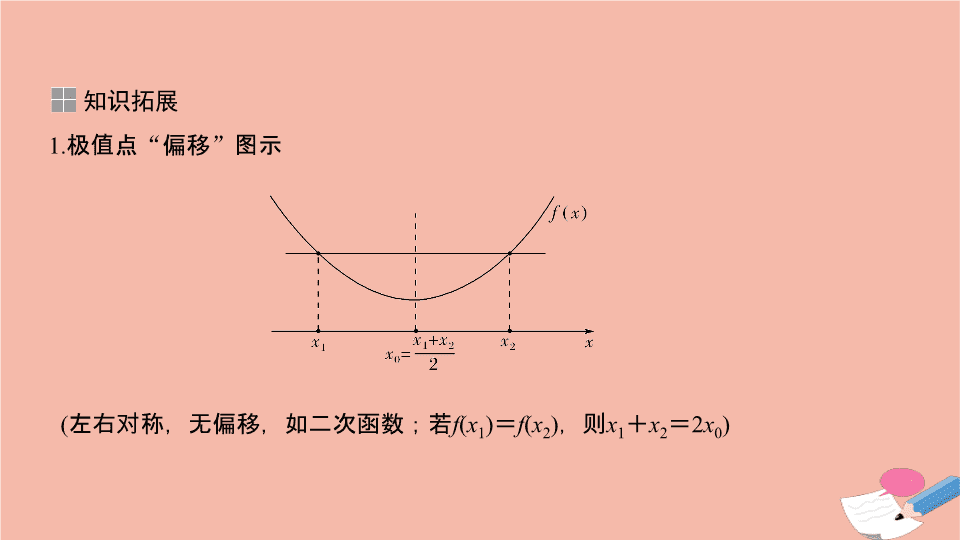
极值点的 “ 偏移 ” 问题 1. 极值点 “ 偏移 ” 图示 知识拓展 ( 左右对称,无偏移,如二次函数;若 f ( x 1 ) = f ( x 2 ) ,则 x 1 + x 2 = 2 x 0 ) ( 左陡右缓,极值点向左偏移;若 f ( x 1 ) = f ( x 2 ) ,则 x 1 + x 2 > 2 x 0 ) ( 左缓右陡,极值点向右偏移;若 f ( x 1 ) = f ( x 2 ) ,则 x 1 + x 2 < 2 x 0 ) 【例 1 】 已知函数 f ( x ) = x e - x . (1) 求函数 f ( x ) 的单调区间和极值; (2) 已知函数 g ( x ) 的图象与 f ( x ) 的图象关于直线 x = 1 对称,证明:当 x > 1 时, f ( x ) > g ( x ) ; (3) 如果 x 1 ≠ x 2 ,且 f ( x 1 ) = f ( x 2 ) ,证明: x 1 + x 2 > 2. 题型一 对称化构造法 题型突破 (2) 证明 由 g ( x ) 的图象与 f ( x ) 的图象关于直线 x = 1 对称,得 g ( x ) 的解析式为 y = f (2 - x ) ,构造辅助函数 F ( x ) = f ( x ) - g ( x ) = f ( x ) - f (2 - x ) , x ∈ (1 ,+ ∞ ) , 求导得 F ′( x ) = f ′( x ) - [ f (2 - x )]′ = e - x (1 - x ) + e x - 2 ( x - 1) = ( x - 1)(e x - 2 - e - x ) , 当 x > 1 时, x - 1 > 0 , e x - 2 - e - x > 0 ,则 F ′( x ) > 0 ,得 F ( x ) 在 (1 ,+ ∞ ) 上单增,有 F ( x ) > F (1) = 0 ,即 f ( x ) > g ( x ). (3) 证明 由 f ( x 1 ) = f ( x 2 ) ,结合 f ( x ) 的单调性可设 x 1 < 1 < x 2 ,将 x 2 代入 (2) 中不等式得 f ( x 2 ) > f (2 - x 2 ) ,又 f ( x 1 ) = f ( x 2 ) ,故 f ( x 1 ) > f (2 - x 2 ) ,又 x 1 < 1 , 2 - x 2 < 1 , f ( x ) 在 ( - ∞ , 1) 上单增,故 x 1 > 2 - x 2 , x 1 + x 2 > 2. 【训练 1 】 (2016· 新课标 Ⅰ 卷节选 ) 已知函数 f ( x ) = ( x - 2)e x + a ( x - 1) 2 有两个零点 ( a > 0). 设 x 1 , x 2 是 f ( x ) 的两个零点,证明: x 1 + x 2 <2. 证明 由 f ′( x ) = ( x - 1)e x + 2 a ( x - 1) = ( x - 1)(e x + 2 a ) ,知 f ( x ) 在 ( - ∞ , 1) 上递减,在 (1 ,+ ∞ ) 上递增, f (1) =- e ,由 f ( x 1 ) = f ( x 2 ) = 0 ,可设 x 1 < 1 < x 2 . 构造辅助函数 F ( x ) = f ( x ) - f (2 - x ) ,求导得 F ′( x ) = f ′( x ) - [ f (2 - x )]′ = ( x - 1)(e x + 2 a ) - ( x - 1)(e 2 - x + 2 a ) = ( x - 1)(e x - e 2 - x ) , 当 x < 1 时, x - 1 < 0 , e x - e 2 - x < 0 ,则 F ′( x ) > 0 ,得 F ( x ) 在 ( - ∞ , 1) 上单增,又 F (1) = 0 ,故 F ( x ) < 0( x < 1) ,即 f ( x ) < f (2 - x )( x < 1). 将 x 1 代入上述不等式中,得 f ( x 1 ) = f ( x 2 ) < f (2 - x 1 ) ,又 x 2 > 1 , 2 - x 1 > 1 , f ( x ) 在 (1 ,+ ∞ ) 递增,故 x 2 < 2 - x 1 , x 1 + x 2 < 2. 题型二 构造函数的选取 【例 2 】 已知函数 f ( x ) = e x - ax 有两个不同的零点 x 1 , x 2 ,其极值点为 x 0 . (1) 求 a 的取值范围; (2) 求证: x 1 + x 2 < 2 x 0 ; (3) 求证: x 1 + x 2 > 2 ; (4) 求证: x 1 x 2 < 1. (1) 解 f ′( x ) = e x - a ,若 a ≤ 0 ,则 f ′( x ) > 0 , f ( x ) 在 R 上单增, f ( x ) 至多有 1 个零点,舍去;故必有 a > 0 ,易得 f ( x ) 在 ( - ∞ , ln a ) 上单减,在 (ln a ,+ ∞ ) 上单增,要使 f ( x ) 有两个不同的零点,则有 f (ln a ) < 0 ⇒ a > e( 严格来讲,还需补充两处变化趋势的说明:当 x → - ∞ 时, f ( x ) → + ∞ ;当 x → + ∞ 时, f ( x ) → + ∞ ). (2) 证明 由所证结论知这是 f ( x ) 的极值点偏移问题,选取函数 f ( x ) 来做,下面按对称化构造的三个步骤来写,其中 x 0 = ln a . ① 由 (1) 知 f ( x ) 在 ( - ∞ , x 0 ) 上单减,在 ( x 0 ,+ ∞ ) 上单增,可设 x 1 < x 0 < x 2 ; ② 构造函数 F ( x ) = f ( x ) - f (2 x 0 - x ) ,则 F ′( x ) = f ′( x ) - [ f (2 x 0 - x )]′ = e x + e 2 x 0 - x - 2 a , ③ 将 x 1 代入 ② 中不等式得 f ( x 1 ) = f ( x 2 ) < f (2 x 0 - x 1 ) ,又 x 2 > x 0 , 2 x 0 - x 1 > x 0 , f ( x ) 在 ( x 0 ,+ ∞ ) 上单增,故 x 2 < 2 x 0 - x 1 , x 1 + x 2 < 2 x 0 . (4) 证明 ① 同上; 【训练 2 】 已知 b > a > 0 ,且 b ln a - a ln b = a - b . 求证: (1) a + b - ab > 1 ; (2) a + b > 2. 当 x ∈ (0 , 1) 时, (2 - x ) 2 ln x + x 2 ln(2 - x ) 的符号如何判定? 尝试变更结论:证明更强的结论 ab > 1. 题型三 变更结论 规律方法 通过换元化为常规类型证明 【训练 3 】 已知函数 f ( x ) = ln x 和 g ( x ) = ax ,若存在两个实数 x 1 , x 2 ,且 x 1 ≠ x 2 ,满足 f ( x 1 ) = g ( x 1 ) , f ( x 2 ) = g ( x 2 ) ,求证: x 1 x 2 > e 2 . 证明 令 x 1 > x 2 > 0 , ∵ f ( x 1 ) = g ( x 1 ) , f ( x 2 ) = g ( x 2 ) , ∴ ln x 1 - ax 1 = 0 , ln x 2 - ax 2 = 0 ,查看更多