2017-2018学年宁夏育才中学高二下学期期中考试数学（文）试题 Word版

2017-2018学年宁夏育才中学高二下学期期中考试数学（文）试题 Word版

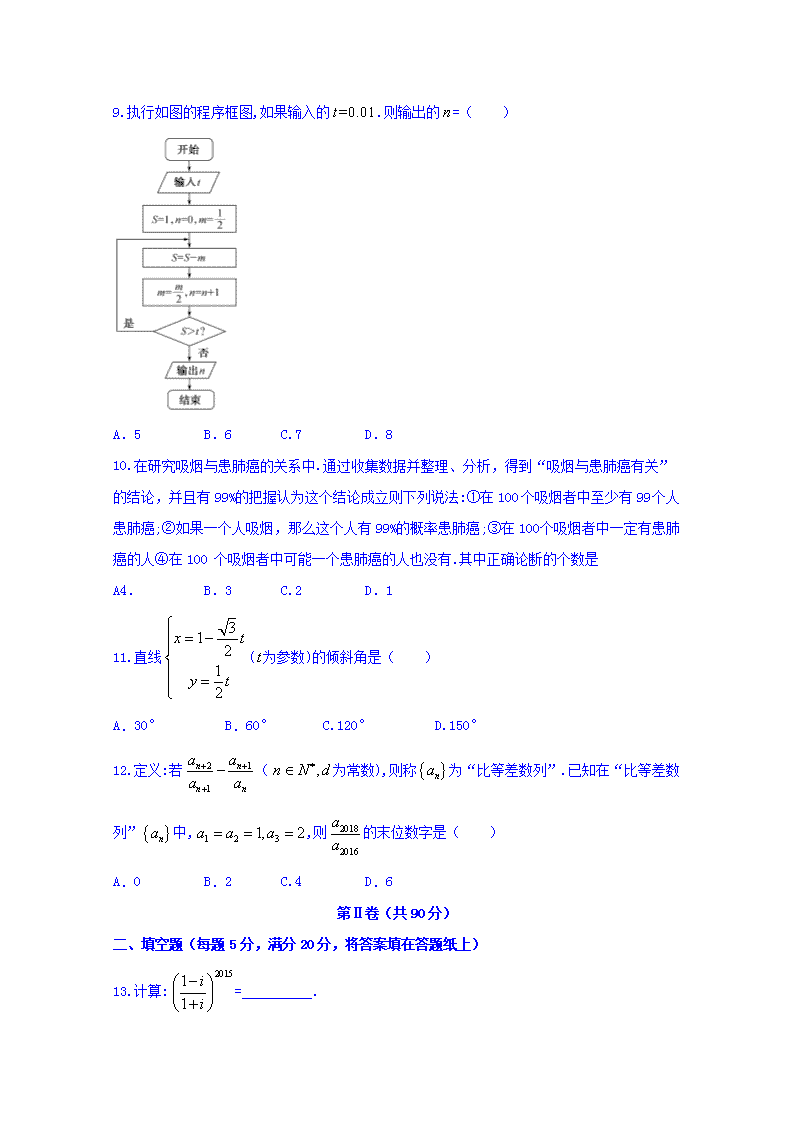
‎2017-2018学年宁夏育才中学高二下学期期中考试 数学试卷(文科)‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知为虚数单位,若复数满足.则的虚部是（ ）‎ A．-2 B．4 C．3 D．-4‎ ‎2.将极坐标化为直角坐标是（ ）‎ A． B． C． D．‎ ‎3.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则该回归直线的方程是（ ）‎ A． B． C． D． ‎ ‎4.已知为虚数单位,复数,且是实数,则实数等于（ ）‎ A． B． C. D．‎ ‎5.圆的半径是（ ）‎ A．1 B． C. D．2‎ ‎6.已知是虚数单位,则复数在复平面内所对应的点位于（ ）‎ A．第一象限 B．第二象限 C.第三象限 D．第四象限 ‎7..下列关于残差图的叙述错误的是 A.通过残差图可以发现原始数据中的可疑数据,判断所建模型的拟合效果 B.残差图的纵坐标只能是残差,横坐标可以是编号,解释变量,也可以是预报变量 C.残差点分布的带状区域的宽度越窄,模型拟合精度越高,预报精度越高 D.残差点分布的带状区域的宽度越窄,残差平方和越小,相关指数越小 ‎8.参数方程（为参数)化为普通方程是 A． B． C. D．‎ ‎9.执行如图的程序框图,如果输入的.则输出的=（ ）‎ A．5 B．6 C.7 D．8‎ ‎10.在研究吸烟与患肺癌的关系中.通过收集数据并整理、分析，得到“吸烟与患肺癌有关”的结论，并且有99%的把握认为这个结论成立则下列说法:①在100 个吸烟者中至少有99 个人患肺癌;②如果一个人吸烟，那么这个人有99%的概率患肺癌;③在100 个吸烟者中一定有患肺癌的人④在100 个吸烟者中可能一个患肺癌的人也没有.其中正确论断的个数是 A4． B．3 C.2 D．1‎ ‎11.直线(为参数)的倾斜角是（ ）‎ A．30° B．60° C.120° D.150°‎ ‎12.定义:若（ 为常数),则称为“比等差数列”.已知在“比等差数列”中,,则的末位数字是（ ）‎ A．0 B．2 C.4 D．6‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.计算:= ．‎ ‎14.某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100 名电视观众,相关的数据如下表(单位:人)所示:‎ 收看文艺节目 收看新闻节目 总计 ‎20至40岁 ‎40‎ ‎18‎ ‎58‎ 大于40岁 ‎15‎ ‎27‎ ‎42‎ 总计 ‎55‎ ‎45‎ ‎100‎ 由表中数据直观分析,收看新闻节目的观众是否与年龄有关:__________（填“是”或“否”）‎ ‎15.在极坐标系中，点到直线的距离为 ．‎ ‎16.点为此线上任意一点,则的最大值是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.设是实数,若复数(为虛数单位)在复平面内对应的点在直线上,求的值. ‎ ‎18.在对人们休闲方式的一次调查中，共调查了124 人,其中女性70 人,男性54 人。女性中有43人主要的休闲方式是看电视,另外27 人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33 人主要的休闲方式是运动.能否在犯错概率不招过0.025 的前提下判断性别与休闲方式有关系? ‎ 附：‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎19.已知函数在上是增函数..‎ ‎(1)求证:如果,那么;‎ ‎(2)判断(1)中的命题的逆命题是否成立,并证明你的结论. ‎ ‎20.某班5 名学生的数学和物理成绩(单位:分)如下表:‎ 数学成绩 ‎88‎ ‎76‎ ‎73‎ ‎66‎ ‎63‎ 物理成绩 ‎78‎ ‎65‎ ‎71‎ ‎64‎ ‎61‎ ‎(1)画出散点图;‎ ‎(2)求物理成绩对数学成绩的回直线方程;‎ ‎(3)一名学生的数学成绩是96分,试预测他的物理成绩.‎ 附：‎ ‎21.设为虚数,是实数.且.‎ ‎(1)求及的实部的取值范围;‎ ‎(2)若,求证:为纯虚数. ‎ ‎22.在平面直角坐标系中,直线的参数方程为(为参数)，以坐标原点为极点，轴的正半轴为极轴且取相同的单位长度建立极坐标系.已知曲线的极坐标方程为 ‎(1)求曲线的直角坐标方程;‎ ‎(2)若直线与曲线交于两点,且.求直线的倾斜角的值.‎ 宁夏育才中学高二年级期中考试 数学试卷(文科)‎ 一、选择题 ‎1-5:BACAA 6-10:BDCCD 11、12：DB 二、填空题 ‎13.原式= 14.是 因为在20至40岁的58名观众中有18名观众收看新闻节目,而大于40 岁的42名观众中有27 名观众收看新闻,即,两者相差较大,所以经直观分析，收看新闻节目的观众与年龄是有关的. ‎ ‎15.1 ‎ ‎16.‎ 三、解答题 ‎17.解:，‎ 又因为复数(为虚数单位)在复平面内对应的点在直线上，‎ 所以，解得 ‎18.解:建立列联表(单位:人)如下:‎ 休闲方式为看电视 休闲方式为运动 合计 女性 ‎43‎ ‎27‎ ‎70‎ 男性 ‎21‎ ‎33‎ ‎54‎ 合计 ‎64‎ ‎60‎ ‎124‎ ‎∵，，‎ ‎∴‎ 即在犯错慨率不超过0.025的前提下，认为性别与休闲方式有关系.‎ ‎19.(1)证明:当时.且》‎ 因为在上是增函数,所以 故 ‎ ‎(2)解:（1）中命题的逆命题:如果，那么.此命题成立.‎ 证明:假设.则,从而.同理可得 从而有.这与矛盾.故假设不立 故成立.即(1)中命题的逆命题成立.‎ ‎20.解:(1)散点图如图:‎ ‎(2)，‎ ‎.‎ ‎.‎ ‎.‎ 所以.‎ ‎(3),则.即可以预测他的物理成绩是82分 ‎21.(1)解:设.则 因为.所以，又，所以.所以.‎ 所以 又,即.解得.‎ 所以的实部的取值范围的取值范围为.‎ ‎(2)证明:‎ 因为.所以 所以为纯虚数.‎ ‎22.解:(1)由曲线的极坐标方程为.得.‎ 由得曲线直角坐标方程是 ‎(2)将代入曲线的方程得.‎ 化简得 设两点对应的参数分别为.则，‎ ‎∴‎ ‎∴.得，解得或.‎ 故直线的倾斜角的值为或.‎ ‎ ‎