【数学】2020届一轮复习人教A版第28课三角函数的图象与性质(2)学案(江苏专用)
____第28课__三角函数的图象与性质(2)____
1. 会利用“五点法”熟练画出y=Asin(ωx+φ)(A>0,ω>0)的简图.
2. 能由y=sinx的图象通过平移、伸缩等变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象.
3. 能用y=sinx的图象与性质来研究y=Asin(ωx+φ)的图象与性质.
1. 阅读:必修4第34~39页.
2. 解悟:①函数y=Asin(ωx+φ)的图象与y=sinx的图象有什么关系?②怎样画出y=Asin(ωx+φ)(A>0,ω>0)的简图?③你能用y=sinx的图象与性质来研究y=Asin(ωx+φ)的图象与性质吗?④你能领会必修4第35~37页的三个思考的意图吗?例1的作用是什么?
3. 践习:在教材空白处,完成必修4第39~40页练习第 2、3、5、7题.
基础诊断
1. 将函数y=sinx图象上的所有点向右平行移动个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变),所得图象的函数的解析式为__y=sin__.
解析:将函数y=sinx的图象上所有的点向右平行移动个单位长度,得到函数y=sin的图象,再把所得图象中各点的横坐标变为原来的2倍,得到函数y=sin(-)的图象.
2. 要得到函数y=sin3x+cos3x的图象,可以将函数y=sin3x的图象向__左__平移____个单位长度.
解析:因为函数y=sin3x+cos3x=sin=sin,所以将函数y=sin3x的图象向左平移个单位长度可得函数y=sin3x+cos3x的图象.
3. 函数y=sin图象的对称中心为,k∈Z__,对称轴为__x=+,k∈Z__.
解析:因为2x+=kπ,k∈Z,所以x=-,k∈Z,所以函数y=sin的图象的对称中心为,k∈Z.因为2x+=kπ+,k∈Z,所以x=+,k∈Z,
所以函数y=sin的图象的对称轴方程为x=+,k∈Z.
4. 函数y=2sin(0≤x≤9)的最大值与最小值之和为__2-__.
解析:因为0≤x≤9,所以-∈,所以2sin∈[-,2],
所以函数y=2sin(0≤x≤9)的最大值与最小值之和为2-.
范例导航
考向❶ “五点法”与“变换法”作图
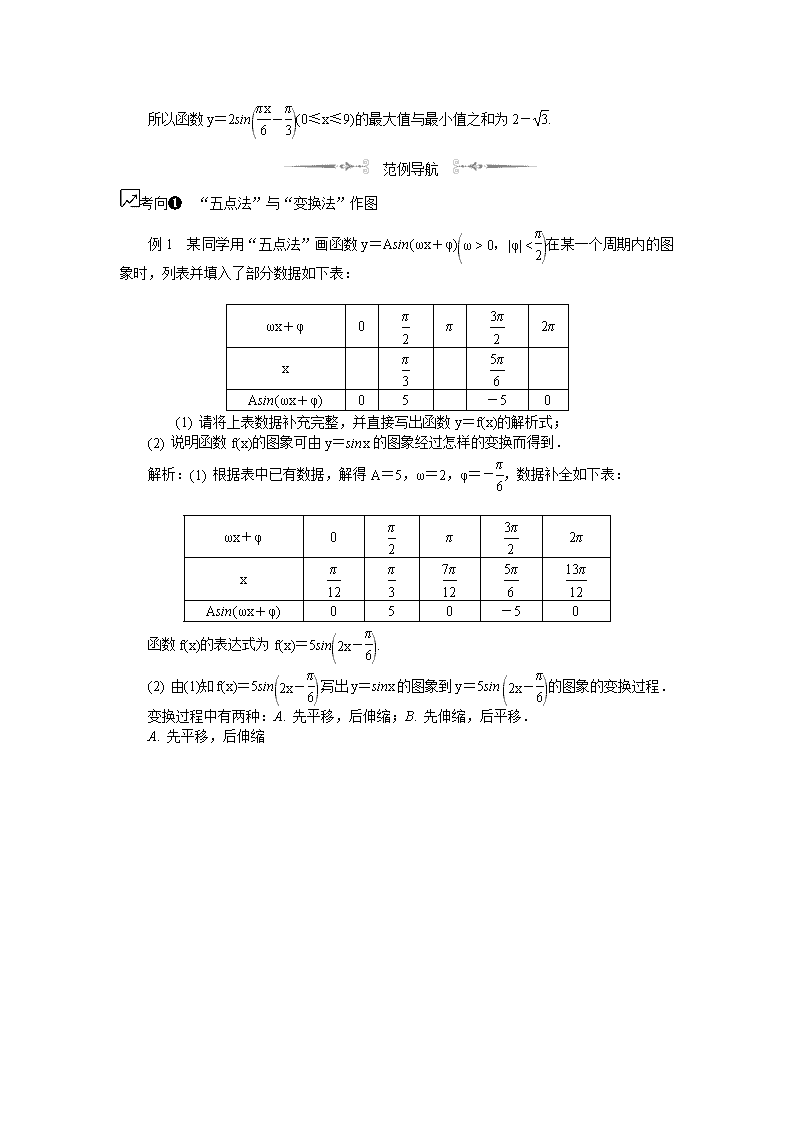
例1 某同学用“五点法”画函数y=Asin(ωx+φ)在某一个周期内的图象时,列表并填入了部分数据如下表:
ωx+φ
0
π
2π
x
Asin(ωx+φ)
0
5
-5
0
(1) 请将上表数据补充完整,并直接写出函数y=f(x)的解析式;
(2) 说明函数f(x)的图象可由y=sinx的图象经过怎样的变换而得到.
解析:(1) 根据表中已有数据,解得A=5,ω=2,φ=-,数据补全如下表:
ωx+φ
0
π
2π
x
Asin(ωx+φ)
0
5
0
-5
0
函数f(x)的表达式为f(x)=5sin.
(2) 由(1)知f(x)=5sin,写出y=sinx的图象到y=5sin的图象的变换过程.
变换过程中有两种:A. 先平移,后伸缩;B. 先伸缩,后平移.
A. 先平移,后伸缩
【注】 “五点法”作图看似简单,却蕴含着三角函数中的整体到个别,再由个别反射到整体的“运算”.
已知f(x)=cos(ωx+φ)(ω>0,-<φ<0)的最小正周期为π,且f=.
(1) 求ω和φ的值;
(2) 在坐标系中作出函数f(x)在[0,π]上的图象;
(3) 若f(x)>,求x的取值范围.
解析:(1) 周期T==π,所以ω=2.
因为f=cos=cos
=-sinφ=.
又-<φ<0,所以φ=-.
(2) 由(1)得f(x)=cos,列表如下:
x
0
π
2x-
-
0
π
f(x)
1
0
-1
0
图象如图:
(3) cos>,
所以2kπ-<2x-<2kπ+,k∈Z,
所以2kπ+<2x<2kπ+,k∈Z,
所以kπ+
0,ω>0,|φ|<π)的图象,由图中条件,写出该函数的解析式.
【点评】 由三角函数图象确定解析式是前几年命题的一个热点,此类型题要充分挖掘给出图象的信息进行求解,首先根据图象可知A=5,函数的周期T=2=3π,所以ω==.
方法一(单调性法):
因为由图象可知点(π,0)在单调递减的那段曲线上,
所以+φ=2kπ+π(k∈Z),
所以φ=2kπ+(k∈Z).
因为|φ|<π,所以φ=.
故所求函数的解析式为y=5sin.
方法二(最值点法):
将最高点坐标代入y=5sinx+φ得5sin=5,
所以+φ=2kπ+(k∈Z),
所以φ=2kπ+(k∈Z),取k=0时得满足|φ|<π的φ=,
故所求函数的解析式为y=5sin.
方法三(零点法):
函数y=Asin(ωx+φ)的图象一般由“五点法”作出,一个周期内至少两个零点.
根据y=Asin(ωx+φ)的图象可知(π,0)是一个周期内的第二个零点,而是下一个周期的第一个零点,于是有+φ=π,解得φ=,
故所求函数的解析式为y=5sin.
方法四(平移法):
由图象可知,起始点坐标是,
则将y=5sin的图象沿x轴向左平移个单位长度,就得到本题图象,
故所求函数的解析式为y=5sin,
即y=5sin.
【反思】 以上各种方法各有所长,方法三可以推广为关键点法,用此法解题要深刻理解五点作图法的本质,即五点之间的对应关系要明确. 进行三角函数图象变换若把函数y=Asin(ωx+φ)的形式平移变换、伸缩变换的次序不同,则平移单位就不同,需要特别注意.
【总结】 已知三角函数y=Asin(ωx+φ)的图象,欲求其解析式,必须搞清A,ω,φ与图象的哪些因素有关,在利用图象与x轴的交点时,要考虑这个点是在增区间上还是在减区间上,否则很容易出错.数形结合的思想方法必须时刻牢记在心,并随时加以运用.
考向❷ 根据图象和性质确定函数y=Asin(ωx+φ)的解析式
例2 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<,x∈R)的部分图象如图所示.
(1) 求函数y=f(x)的解析式;
(2) 当x∈时,求f(x)的取值范围.
解析:(1) 由图象知A=2.
又=-=,ω>0,所以T=2π=,得ω=1,所以f(x)=2sin(x+φ).将点代入,得+φ=+2kπ(k∈Z),即φ=+2kπ(k∈Z).
又-<φ<,所以φ=,
所以f(x)=2sin.
(2) 当x∈[-,]时,x+∈[-,],
所以sin∈,
即f(x)∈[-,2].
已知函数f(x)=sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两条相邻对称轴间的距离为.
(1) 求f的值;
(2) 将函数y=f(x)的图象向右平移个单位长度后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到y=g(x)的图象,求函数g(x)的单调减区间.
解析:(1) 由题可得,f(x)=2sin.
因为f(x)为偶函数,
所以φ-=kπ+,k∈Z,解得φ=kπ+,k∈Z.
因为0<φ<π,所以φ=.由题意得=2×,解得ω=2.
故f(x)=2cos2x,f=2cos=.
(2) 将f(x)的图象向右平移个单位长度后,得到f的图象,再将所得图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得f的图象,所以g(x)=f=
2cos[2(-)]=2cos,
当2kπ≤-≤2kπ+π,k∈Z,即4kπ+≤x≤4kπ+,k∈Z时,函数g(x)单调递减.
故函数g(x)的单调减区间为[4kπ+,4kπ+](k∈Z).
考向❸ 函数y=Asin(ωx+φ)(A>0,ω>0)性质的综合应用
例3 已知函数f(x)=2sin2-cos2x-1,x∈R.
(1) 求函数f(x)的最小正周期;
(2) 若h(x)=f(x+t)的图象关于点对称,且t∈(0,π),求t的值;
(3) 当x∈时,不等式<3恒成立,求实数m的取值范围.
解析:(1) 函数可化为f(x)=-cos-cos2x=sin2x-cos2x=2sin.
故函数f(x)的最小正周期为π.
(2) h(x)=f(x+t)=2sin.
令2×+2t-=kπ,k∈Z,得t=+,k∈Z.
又t∈(0,π),故t=或.
(3) 当x∈时,2x-∈[,],
所以f(x)∈[1,2].
|f(x)-m|<3,即f(x)-3f(π),则函数f(x)的单调减区间是[kπ-,kπ+](k∈Z).
解析:若f(x)≤|f|对x∈R恒成立,则f为函数的最大值或最小值,即2×+φ=kπ+,k∈Z,则φ=kπ+,k∈Z.又因为f>f(π),即-sinφ>sinφ,sinφ<0,令k=-1,此时φ=-,满足条件sinφ<0,令2x-∈[2kπ-,2kπ-](k∈Z),解得x∈[kπ-,kπ+](k∈Z),所以函数f(x)的单调减区间是[kπ-,kπ+](k∈Z).
4. 已知函数y=cosx与函数y=sin(2x+φ)(0≤φ<π)图象有一个横坐标为的交点,则φ的值为____.
解析:由题意得,sin=cos=.因为0≤φ<π,所以≤+φ<,所以+φ=,解得φ=.
1. 三种题型:①已知三角函数的图象,求函数的解析式;②已知三角函数的解析式,求函数的性质(周期、对称性、单调性、最值);③三角函数的变换(注意变换的顺序).
2. 两种思想:化归思想,数形结合思想.
3. 你还有哪些体悟,写下来: