高中数学选修2-2课件数学：1_3《函数的最值与导数》课件（新人教A版选修2-2）

高中数学选修2-2课件数学：1_3《函数的最值与导数》课件（新人教A版选修2-2）

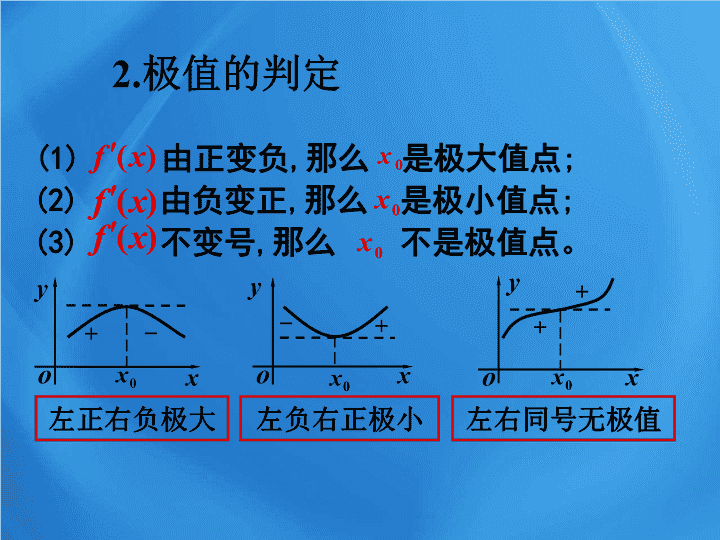
函数的最值与导数 1 、导数与单调性的关系 复习 左正右负极大 左负右正极小 左右同号无极值 (2) 由负变正 , 那么 是极小值点 ; (3) 不变号 , 那么 不是极值点。 (1) 由正变负 , 那么 是极大值点 ; 2. 极值的判定 (1)     求导函数 f ˊ( x ) ； (2)    求解方程 f ˊ( x )=0 ； (3)   检查 f ˊ( x ) 在方程 f ˊ( x )=0 的根的左右的符号，并根据符号确定极大值与极小值 . 口诀： 左负右正为极小，左正右负为极大 . 用导数法求解函数极值的 步骤： 复习 求函数最值 1) 在某些问题中，往往关心的是函数在整个定义域区间上，哪个值最大或最小的问题这就是我们通常所说的 最值问题 . 2) 在 闭区间 [ a , b ] 上的函数 y = f ( x ) 的图象是一条 连续不断 的曲线 , 则它 必有 最大值和最小值 . x y 0 a b x 1 x 2 x 3 x 4 f ( a ) f ( x 3 ) f ( b ) f ( x 1 ) f ( x 2 ) 新课 o x y a b o x y a b o y o x y a b y = f ( x ) y = f ( x ) y = f ( x ) x a b y = f ( x ) 归纳结论： （ 1 ）函数 f （ x ）的图像若在开区间（ a ， b ）上是连续不断的曲线，则函数 f （ x ）在（ a ， b ）上不一定有最大值或最小值；函数在半开半闭区间上的最值亦是如此 （ 2 ）函数 f （ x ）若在闭区间 [a ， b] 上有定义，但有间断点，则函数 f （ x ）也不一定有最大值或最小值 总结：一般地，如果在区间 [a ， b] 上 函数 f （ x ）的图像是一条连续不断的曲线，那么它 必 有最大值和最小值 。如何求最值？ 只要把连续函数的所有极值与端点的函数值进行比较，就可求最大值、最小值 解 : 当 变化时 , 的变化情况如下表 : 例 1 、求函数 在区间 上的最大 值与最小值。 令 , 解得 又由于 （ 舍去 ） － ＋ ↗ ↘ 极小值 应用 函数在区间 上最大值为 , 最小值为 例 2 ： 已知函数 (1) 求 的单调减区间 (2) 若 在区间 上的最大值为 , 求该区间上的最小值 所以函数的单调减区间为 解 : 应用 令 解得 当 变化时 , 的变化情况如下表 : （舍去） ↘ -- ↗ 极小值 最小值为 所以函数的最大值为 , 最小值为 (2) 将 y = f ( x ) 的各极值与 f ( a ) 、 f ( b )( 端点处 ) 比较 , 其中最大的一个为最大值，最小的 一个最小值 . 求 f ( x ) 在 闭区间 [ a , b ] 上的最值的步骤 (1) 求 f ( x ) 在区间 ( a , b ) 内极值 ( 极大值或极小值 ) 小结 解 : 令 解得 所以函数的极大值为 ，极小值为 1 、已知函数 (1) 求 的极值 (2) 当 在什么范围内取值时，曲线 与 轴总有交点 当 变化时 , 的变化情况如下表 : ↘ -- + ↗ ↘ -- 极小值 极大值 练习 曲线 与 轴总有交点 由（ 1 ）可知，函数在区间 上的极大值为 ，极小值为 ，又因 ， (2) 所以函数的最大值为 ，最小值为 2 、求函数 f ( x )=3 x - x 3 在区间 [-3 ， 3] 内的最大值和最小值 . 练习 一 . 是利用函数性质 二 . 是利用不等式 三 . 是利用导数 注： 求函数最值的一般方法 课本 32 页 第 6 题 (1)(2)(3) 课后作业