- 2021-07-01 发布 |
- 37.5 KB |
- 11页
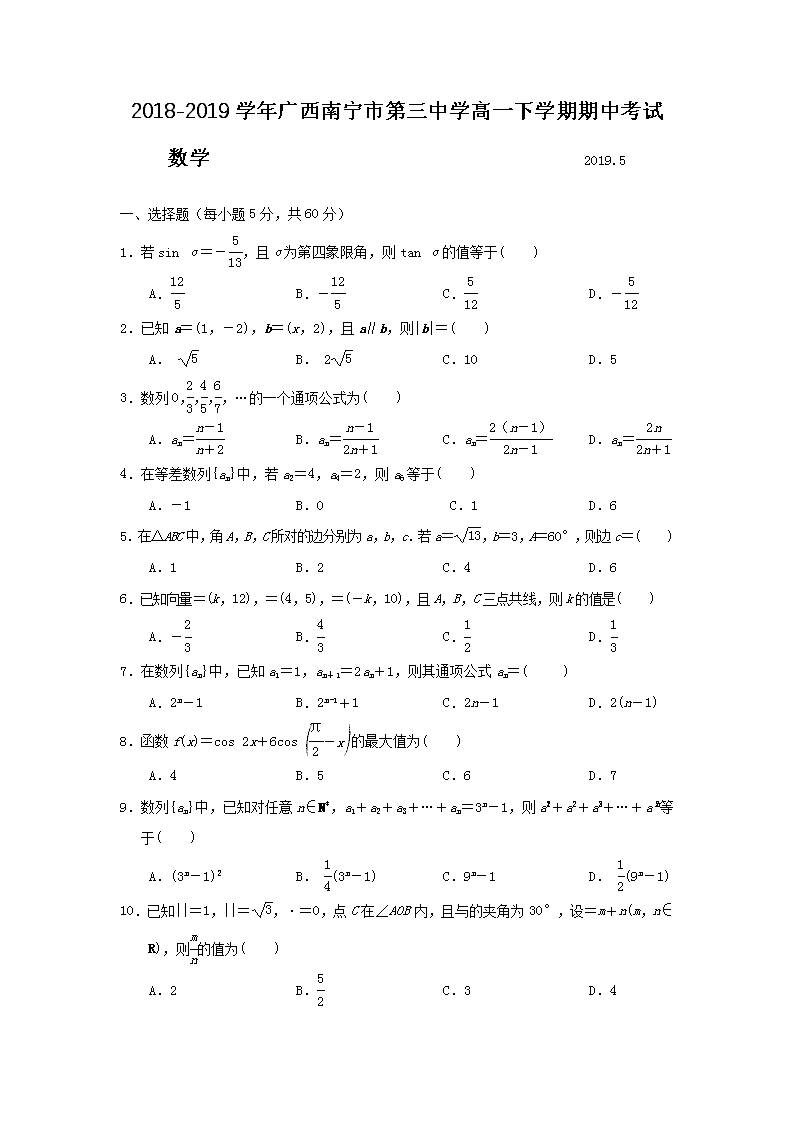


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年广西南宁市第三中学高一下学期期中考试 数学 解析版
2018-2019学年广西南宁市第三中学高一下学期期中考试 数学 2019.5 一、选择题(每小题5分,共60分) 1.若sin α=-,且α为第四象限角,则tan α的值等于( ) A. B.- C. D.- 2.已知a=(1,-2),b=(x,2),且a∥b,则|b|=( ) A. B. 2 C.10 D.5 3.数列0,,,,…的一个通项公式为( ) A.an= B.an= C.an= D.an= 4.在等差数列{an}中,若a2=4,a4=2,则a6等于( ) A.-1 B.0 C.1 D.6 5.在△ABC中,角A,B,C所对的边分别为a,b,c.若a=,b=3,A=60°,则边c=( ) A.1 B.2 C.4 D.6 6.已知向量=(k,12),=(4,5),=(-k,10),且A,B,C三点共线,则k的值是( ) A.- B. C. D. 7.在数列{an}中,已知a1=1,an+1=2an+1,则其通项公式an=( ) A.2n-1 B.2n-1+1 C.2n-1 D.2(n-1) 8.函数f(x)=cos 2x+6cos的最大值为( ) A.4 B.5 C.6 D.7 9.数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则a+a+a+…+a等于( ) A.(3n-1)2 B. (3n-1) C.9n-1 D. (9n-1) 10.已知||=1,||=,·=0,点C在∠AOB内,且与的夹角为30°,设=m+n(m,n∈R),则的值为( ) A.2 B. C.3 D.4 11.已知函数f(x)=sin(ωx+φ)的最小正周期为4π,且对于任意x∈R,有f(x)≤f 成立,则f(x)图象的一个对称中心坐标是( ) A. B. C. D. 12.已知数列{an}的通项公式为an=(n∈N*),其前n项和为Sn,则在数列S1,S2,…,S2 019中,有理数项的项数为( ) A.42 B.43 C.44 D.45 二、填空题(每小题5分,共20分) 13.设各项都是正数的等比数列{an},Sn为前n项和,且S10=10,S30=70,那么S40=________ 14.在△ABC中,角A,B,C所对的边分别为a,b,c,若角A,B,C依次成等差数列,且a=1,b=,则S△ABC=________. 15.已知向量=(3,-4),=(6,-3),=(5-m,-3-m),若∠ABC为锐角,则实数m的取值范围是________. 16.等差数列{an}的前n项和为Sn,且a2=6,a3+a6=27,设Tn=,若对于一切正整数n,总有Tn≤t成立,则实数t的取值范围是________. 三、解答题(共70分) 17.(本小题满分10分) 已知函数f(x)=(sin x+cos x)2+cos 2x. (1)求f(x)的最小正周期; (2)求f(x)在区间上的最大值和最小值. 18.(本小题满分12分) (1)已知{an}是等差数列,Sn是其前n项和,若a1+a=-3,S5=10,求a9. (2)已知x,y,z∈R,若-1,x,y,z,-3成等比数列,求xyz的值. 19.(本小题满分12分) (1)已知非零向量a,b满足|b|=4|a|,且a⊥(2a+b),求a与b的夹角θ. (2)设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3, =2,求·的值. 20.(本小题满分12分) 在△ABC中,角A,B,C的对边分别为a,b,c,且(2a-b)cos C-ccos B=0. (1)求角C的值; (2)若三边a,b,c满足a+b=13,c=7,求△ABC的面积. 21.(本小题满分12分) 设Sn为等差数列{an}的前n项和,已知S3=a7,a8-2a3=3. (1)求an; (2)设bn=,求数列{bn}的前n项和为Tn. 22.(本小题满分12分) 若数列{an}的前n项和Sn=2an-2. (1)求数列{an}的通项公式; (2)若bn=an·logan,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立, 试求实数m 的取值范围. 高一段考数学试题参考答案 1.D ∵sin α=-,且α为第四象限角,∴tan α=-. 2.A ∵a∥b,∴ x=-1,∴b=(-1,2),∴|b|==. 3.C 分子0,2,4,6都是偶数. 4.B a6=2a4-a2=2×2-4=0. 5.C a2=c2+b2-2cbcos A⇒13=c2+9-2c×3×cos 60°,即c2-3c-4=0, 解得c=4或c=-1(舍). 6.A =-=(4-k,-7),=-=(-2k,-2),因为A,B,C三点共线, 所以,共线,所以-2×(4-k)=-7×(-2k),解得k=-. 7.A 由题意知an+1+1=2(an+1),∴数列{an+1}是以2为首项,2为公比的等比数列, ∴an+1=2n,∴an=2n-1. 8.B 由f(x)=cos 2x+6cos=1-2sin2x+6sin x=-2+, 所以当sin x=1时函数的最大值为5. 9.D ∵a1+a2+…+an=3n-1,n∈N*,n≥2时,a1+a2+…+an-1=3n-1-1, ∴当n≥2时,an=3n-3n-1=2·3n-1,又n=1时,a1=2适合上式, ∴an=2·3n-1,故数列{a}是首项为4,公比为9的等比数列. 因此a+a+…+a==(9n-1). 10.C ∵·=0,∴⊥,以OA为x轴,OB为y轴建立直角坐标系, =(1,0),=(0,),=m+n=(m,n). ∵ tan 30°==,∴ m=3n,即=3. 11.A 由f(x)=sin(ωx+φ)的最小正周期为4π,得ω=.因为f(x)≤f 恒成立, 所以f(x)max=f ,即×+φ=+2kπ(k∈Z),由|φ|<,得φ=, 故f(x)=sin.令x+=kπ(k∈Z),得x=2kπ-(k∈Z), 故f(x)图象的对称中心为(k∈Z), 当k=0时,f(x)图象的对称中心为. 12.B an= = =-. 所以Sn=1-+++…+=1-, 因此S3,S8,S15…为有理项,又下标3,8,15,…的通项公式为bn=n2-1(n≥2), 所以n2-1≤2 019,且n≥2,所以2≤n≤44,所以有理项的项数为43. 13.150 数列S10,S20-S10,S30-S20,S40-S30成等比数列, 因此有(S20-S10)2=S10(S30-S20).即(S20-10)2=10(70-S20), 故S20=-20或S20=30,又S20>0,因此S20=30,S20-S10=20,S30-S20=40, 故S40-S30=80.S40=150. 14. 因为角A,B,C依次成等差数列,所以B=60°.由正弦定理,得=, 解得sin A=,因为0°<A<180°,所以A=30°或150°(舍去),此时C=90°, 所以S△ABC=ab=. 15. ∪ 由已知得=-=(3,1),=-=(2-m,1-m).若∥, 则有3(1-m)=2-m,解得m=. 由题设知,=(-3,-1),=(-1-m,-m). ∵∠ABC为锐角,∴·=3+3m+m>0,可得m>-. 由题意知,当m=时,∥,且与同向. 故当∠ABC为锐角时,实数m的取值范围是∪. 16. 设公差为d,由题意得:解得∴an=3n. 则Sn=3(1+2+3+…+n)=n(n+1),∴Tn=,Tn+1=, ∴Tn+1-Tn=-=, ∴当n≥3时,Tn>Tn+1,且T1=1查看更多