【数学】2018届一轮复习人教A版(理)4-7正弦定理和余弦定理学案
§4.7 正弦定理和余弦定理
考纲展示► 1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.
2.能够运用正弦定理、余弦定理等知识和方法解决一些与测量、几何计算有关的实际问题.
考点1 利用正、余弦定理解三角形
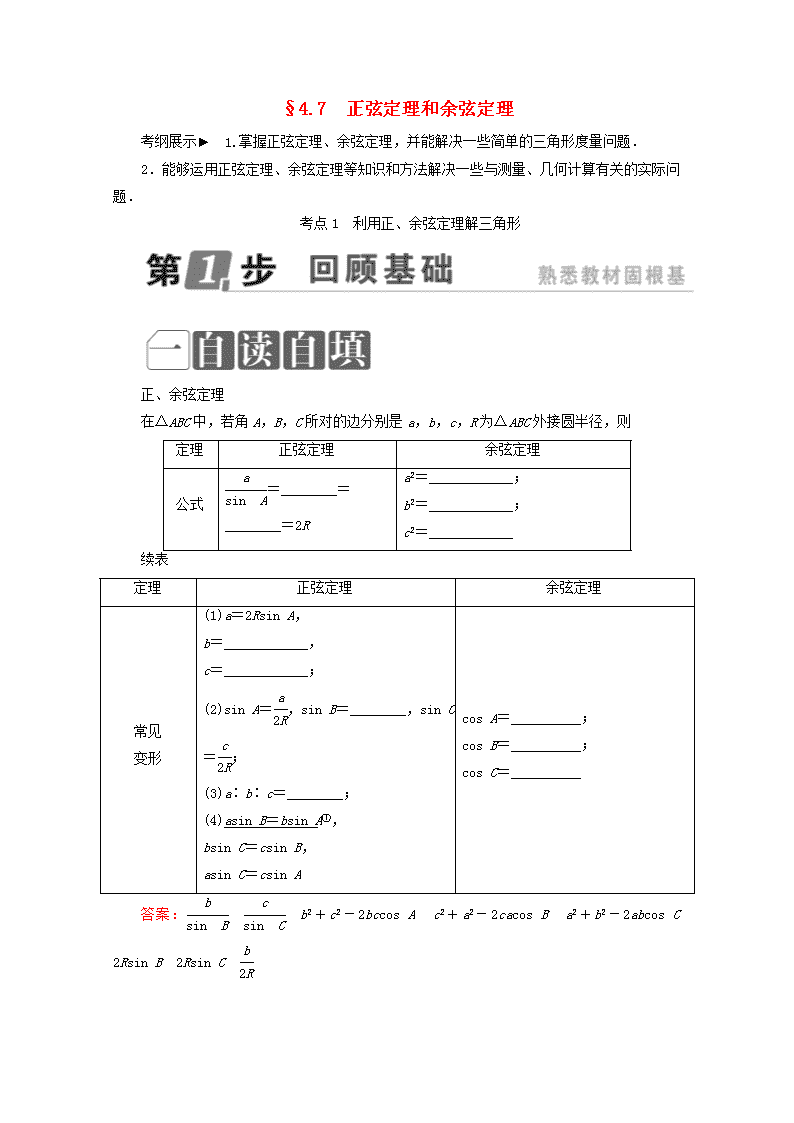
正、余弦定理
在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则
定理
正弦定理
余弦定理
公式
=________=
________=2R
a2=____________;
b2=____________;
c2=____________
续表
定理
正弦定理
余弦定理
常见
变形
(1)a=2Rsin A,
b=____________,
c=____________;
(2)sin A=,sin B=________,sin C=;
(3)a∶b∶c=________;
(4)asin B=bsin A①,
bsin C=csin B,
asin C=csin A
cos A=__________;
cos B=__________;
cos C=__________
答案: b2+c2-2bccos A c2+a2-2cacos B a2+b2-2abcos C 2Rsin B 2Rsin C
sin A∶sin B∶sin C
(1)[教材习题改编]在△ABC中,已知a=5,b=7,c=8,则∠A+∠C=( )
A.90° B.120°
C.135° D.150°
答案:B
(2)[教材习题改编]在△ABC中,已知∠A=60°,∠B=75°,c=20,则a=________.
答案:10
解三角形的一般类型:已知两边及一角;已知两角及一边;已知三边.
(1)在△ABC中,已知a=5,b=2,C=30°,则c=________.
答案:
解析:由余弦定理,得c2=a2+b2-2abcos C=52+(2)2-2×5×2cos 30°=7,所以c=.
(2)在△ABC中,内角A,B,C的对边分别为a,b,c,若B=,sin A=,b=,则a=________.
答案:
解析:由正弦定理=,得a==.
(3)在△ABC中,已知a∶b∶c=2∶4∶3,则cos C=________.
答案:
解析:设a=2k,b=4k,c=3k(k>0),
则cos C==.
[典题1] [2017·山师大附中一模]设△ABC的内角A,B,C的对边分别为a,b,c,且bsin A=acos B.
(1)求角B的大小;
(2)若b=3,sin C=2sin A,求a,c的值.
[解] (1)∵bsin A=acos B,
由正弦定理得sin Bsin A=sin Acos B.
在△ABC中,sin A≠0,
即得tan B=,∴B=.
(2)∵sin C=2sin A,由正弦定理得c=2a,
由余弦定理b2=a2+c2-2accos B,
即9=a2+4a2-2a·2acos ,
解得a=,∴c=2a=2.
[点石成金] 1.解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
2.三角形解的个数的判断:已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.
设△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cos B=.
(1)求a,c的值;
(2)求sin(A-B)的值.
解:(1)由余弦定理,得
cos B===,
即a2+c2-4=ac.
∴(a+c)2-2ac-4=ac,∴ac=9.
由得a=c=3.
(2)在△ABC中,cos B=,
∴sin B===.
由正弦定理,得=,
∴sin A===.
又A=C,∴0<A<,
∴cos A==,
∴sin(A-B)=sin Acos B-cos Asin B
=×-×=.
考点2 利用正弦、余弦定理判定三角形的形状
三角形中的角的关系判断误区:角的大小比较的误区;角的个数的误区.
(1)在△ABC中,若sin A>sin B,则A与B的大小关系是________.
答案:A>B
解析:由正弦定理,得sin A=,sin B=.
若sin A>sin B,则>,即a>b,故A>B.
(2)在△ABC中,若A=60°,a=4,b=4,则B等于________.
答案:45°
解析:由正弦定理,有=,则sin B===.又a>b,所以A>B,故B=45°.
注意挖掘题中隐含条件,以便确定满足条件的角的情况.
判断三角形的形状.
利用正、余弦定理判断三角形的形状,一般都可以通过两种途径实现:(1)把角的条件转化为边,通过边的关系判断;(2)把边的条件转化为角,通过计算角的大小进行判断.
[典题2] (1)在△ABC中,内角A,B,C的对边分别为a,b,c,且2c2=2a2+2b2+ab,则△ABC是( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.等边三角形
[答案] A
[解析]由2c2=2a2+2b2+ab,得
a2+b2-c2=-ab,
所以cos C===-<0,
所以90°<C<180°,即△ABC为钝角三角形.
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
[答案] B
[解析] 依据题设条件的特点,由正弦定理,
得sin Bcos C+cos Bsin C=sin2A,
有sin(B+C)=sin2A,
∵A∈(0,π),∴sin A≠0.
从而sin(B+C)=sin A=sin2A,解得sin A=1,
∴A=,故选B.
[题点发散1] 若将本例条件改为“若2sin Acos B=sin C”,那么△ABC一定是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
答案:B
解析:解法一:由已知得2sin Acos B=sin C=sin(A+B)=sin Acos B+cos Asin B,即sin(A-B)=0,因为-π
0),
由余弦定理可得
cos C===-<0,
又∵C∈(0,π),∴C∈,
∴△ABC为钝角三角形.
[题点发散4] 若将本例条件改为“(a2+b2)sin(A-B)=(a2-b2)sin(A+B)”,试判断三角形的形状.
解:∵(a2+b2)sin(A-B)=(a2-b2)sin(A+B),
∴b2[sin(A+B)+sin(A-B)]=a2[sin(A+B)-sin(A-B)],
∴2sin Acos B·b2=2cos Asin B·a2,
即a2cos Asin B=b2sin Acos B.
解法一:由正弦定理知a=2Rsin A,b=2Rsin B,
∴sin2Acos Asin B=sin2Bsin Acos B,
又sin A·sin B≠0,
∴sin Acos A=sin Bcos B,
∴sin 2A=sin 2B.
在△ABC中,0<2A<2π,0<2B<2π,
∴2A=2B或2A=π-2B,
∴A=B或A+B=.
∴△ABC为等腰三角形或直角三角形.
解法二:由正弦定理、余弦定理,得
a2b=b2a,
∴a2(b2+c2-a2)=b2(a2+c2-b2),
∴(a2-b2)(a2+b2-c2)=0,
∴a2-b2=0或a2+b2-c2=0.
即a=b或a2+b2=c2.
∴△ABC为等腰三角形或直角三角形.
[题点发散5] 若将本例条件改为:“2asin A=(2b+c)·sin B+(2c+b)sin C,且sin B+sin C=1”,试判断△ABC的形状.
解:由已知,根据正弦定理,得
2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc,cos A=-,sin A=,
则sin2A=sin2B+sin2C+sin Bsin C.
解得sin B=sin C=.
故B=C=,
所以△ABC是等腰钝角三角形.
[点石成金] 1.判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是不是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
2.判断三角形形状主要有以下两种途径:
(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断;
(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出三条边之间的关系进行判断.
在△ABC中,角A,B,C所对的边分别为a,b,c,若0,于是有cos B<0,B为钝角,△ABC是钝角三角形.
考点3 与三角形面积有关的问题
三角形中常用的面积公式
(1)S=ah(h表示边a上的高);
(2)S=bcsin A=acsin B=absin C;
(3)S=r(a+b+c)(r为三角形的内切圆半径).
[教材习题改编]在△ABC中,内角A,B,C的对边分别为a,b,c,且a=2,b=3,S△ABC=,则角C的值为________.
答案:60°或120°
解析:由S△ABC=absin C=×2×3sin C=,得sin C=,因为C为三角形ABC的内角,所以C=60°或C=120°.
三角形面积公式.
利用正余弦定理三角形的面积还可以写成:
S=2R2sin Asin Bsin C,
S=.
[典题3] [2017·河北衡水模拟]如图,在△ABC中,sin ∠ABC=,AB=2,点D在线段AC上,且AD=2DC,BD=.
(1)求BC的长;
(2)求△DBC的面积.
[解] (1)因为sin ∠ABC=,
所以cos∠ABC=1-2×=.
在△ABC中,设BC=a,AC=3b,
则由余弦定理可得,9b2=a2+4-a,①
在△ABD和△DBC中,由余弦定理可得,
cos∠ADB=,cos∠BDC
=.
因为cos∠ADB=-cos∠BDC,
所以有=-,
所以3b2-a2=-6.②
由①②可得,a=3,b=1,即BC=3.
(2)由(1)得△ABC的面积为
S=×2×3×=2,所以△DBC的面积为.
[点石成金] 三角形面积公式的应用原则
(1)对于面积公式S=absin C=acsin B=bcsin A,一般是已知哪一个角就使用哪一个公式.
(2)与面积有关的问题,一般要用正弦定理或余弦定理进行边和角的转化.
[2017·湖北武汉质量预测]在△ABC中,角A,B,C的对边分别为a,b,c,且满足a2-b2-c2+bc=0,2bsin A=a,BC边上中线AM的长为.
(1)求角A和角B的大小;
(2)求△ABC的面积.
解:(1)由a2-b2-c2+bc=0,得
b2+c2-a2=bc,
∴cos A==,∴A=,
由2bsin A=a,得b=a,∴B=A=.
(2)设AC=BC=x,由余弦定理,
得AM2=x2+-2x··
=()2,
解得x=2,故S△ABC=×2×2×=2.
真题演练集训
1.[2014·新课标全国卷Ⅱ]钝角三角形ABC的面积是,AB=1 ,BC=,则AC=( )
A.5 B.
C.2 D.1
答案:B
解析:由题意可得AB·BC·sin B=,
又AB=1 ,BC=,所以sin B=,
所以B=45°或B=135°.
当B=45°时,由余弦定理可得
AC==1,
此时AC=AB=1,BC=,易得A=90°,与“钝角三角形”条件矛盾,舍去.所以B=135°.
由余弦定理可得
AC==.
2.[2014·新课标全国卷Ⅰ]已知a,b,c分别为△ABC三个内角A,B,C的对边,a
=2,且(2+b)(sin A-sin B)=(c-b)sin C,则△ABC面积的最大值为________.
答案:
解析:∵===2R,a=2,又(2+b)(sin A-sin B)=(c-b)sin C可化为(a+b)(a-b)=(c-b)c,∴a2-b2=c2-bc,∴b2+c2-a2=bc.
∴===cos A,∴A=60°.
∵△ABC中,4=a2=b2+c2-2bc·cos 60°=b2+c2-bc≥2bc-bc=bc(当且仅当b=c时等号成立),
∴S△ABC=·bc·sin A≤×4×=.
3.[2016·新课标全国卷Ⅱ]△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b=________.
答案:
解析:解法一:因为cos A=,cos C=,
所以sin A=,sin C=,
从而sin B=sin(A+C)=sin Acos C+cos Asin C
=×+×=.
由正弦定理=,得b==.
解法二:因为cos A=,cos C=,
所以sin A=,sin C=,
从而cos B=-cos(A+C)=-cos Acos C+sin Asin C=-×+×=.
由正弦定理=,得c==.
由余弦定理b2=a2+c2-2accos B,得b=.
解法三:因为cos A=,cos C=,所以sin A=,sin C=,
由正弦定理=,得c==.
从而b=acos C+ccos A=.
解法四:如图,作BD⊥AC于点D,
由cos C=,a=BC=1,知CD=,BD=.
又cos A=,所以tan A=,从而AD=.
故b=AD+DC=.
4.[2016·新课标全国卷Ⅰ]△ABC的内角A,B,C的对边分别为a,b,c,已知2cos C(acos B+bcos A)=c.
(1)求C;
(2)若c=,△ABC的面积为,求△ABC的周长.
解:(1)由已知及正弦定理,得
2cos C(sin Acos B+sin Bcos A)=sin C,
2cos Csin(A+B)=sin C,
故2sin Ccos C=sin C,C∈(0,π).
可得cos C=,所以C=.
(2)由已知,absin C=.
又C=,所以ab=6.
由已知及余弦定理,得a2+b2-2abcos C =7,
故a2+b2=13,从而(a+b)2=25.
所以△ABC的周长为5+.
课外拓展阅读
转化与化归思想在解三角形中的应用
[典例] [2016·新课标全国卷Ⅰ]△ABC的内角A,B,C的对边分别为a,b,c,已知2cos
C(acos B+bcos A)=c.
(1)求C;
(2)若c=,△ABC的面积为,求△ABC的周长.
[审题视角] (1)利用正弦定理进行边角互化求解;(2)利用三角形的面积公式得出ab,再结合余弦定理联立方程求出a+b,进而求得△ABC的面积.
[解] (1)由已知及正弦定理得,
①
2cos Csin(A+B)=sin C.故2sin Ccos C=sin C.
可得cos C=,所以C=.
(2)由已知,得absin C=.
又C=,所以ab=6.
由已知及余弦定理得,a2+b2-2abcos C=7.
故②
所以△ABC的周长为5+.
满分心得
1.(1)题中①处不能利用正弦定理将边化为角,使已知条件中的式子转化为同类.
(2)题中②处不能结合余弦定理将(a+b)视为整体进行求解而走入误区.
2.转化与化归思想在解三角形中的应用主要体现在边角之间利用正、余弦定理统一的转化化简上,使关系式中的量达到统一性.