- 2021-07-01 发布 |
- 37.5 KB |
- 380页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021年新高考数学二轮复习分专题讲义(含解析)
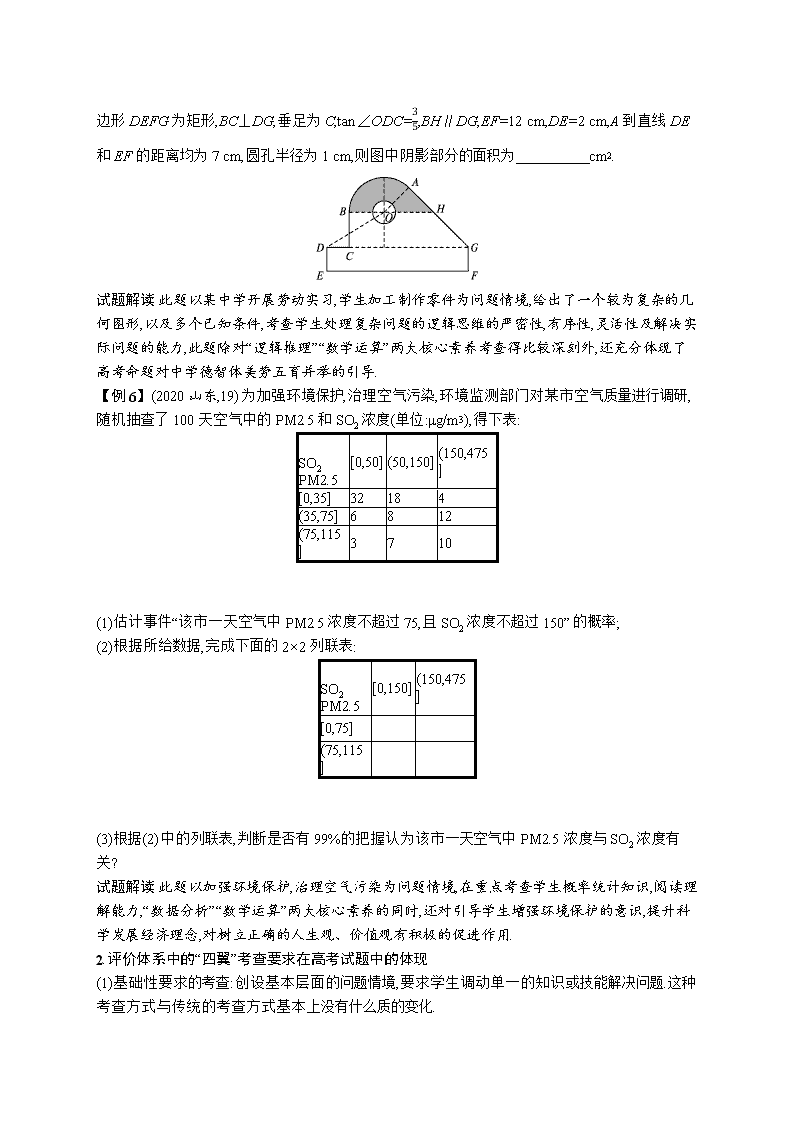
《中国高考评价体系》下的新高考备考 一、高考评价体系的内涵 中国高考评价体系主要由“一核”“四层”“四翼”三部分内容组成.其中,“一核”为高考的核心功能, 即“立德树人、服务选才、引导教学”,是对素质教育中高考核心功能的概括,回答“为什么考”的 问题;“四层”为考查内容,即“核心价值、学科素养、关键能力、必备知识”,是素质教育目标在高 考中的提炼,回答“考什么”的问题;“四翼”为考查要求,即“基础性、综合性、应用性、创新性”,是 素质教育的评价维度在高考中的体现,回答“怎么考”的问题. 二、高考评价体系的重大意义 高考评价体系创造性地将立德树人根本任务融入考试评价全过程,以实现高考评价目标与素质 教育目标的内在统一,切实将高考打造成为立德树人的重要载体和素质教育的关键环节,使之成 为德智体美劳全面培养教育体系的有机组成部分,从而实现“招—考—教—学”全流程各个环节 无缝衔接. 三、高考评价体系对高考命题的指导 为实现高考评价体系的“核心价值引领”,即以立德树人统领服务选才和引导教学,促进学生德智 体美劳全面发展.近几年无论是新课标全国卷,还是高考综合改革省、市的试卷,都遵循了高考评 价体系的精神,在命题理念上逐步实现了从“知识立意”“能力立意”向“价值引领、素养导向、能 力为重、知识为基”的转变,高考评价体系的“一核四层四翼”的内涵已在近年的高考内容改革及 命题当中逐步体现. 四、高考评价体系的要求在高考试题中的体现 认真研读近几年的高考试题,特别是今年的新高考数学山东卷试题,从中能够清晰地感觉到“核心 价值引领”下的高考数学试题,发生了较为深刻的变化.试题落实立德树人根本任务,贯彻德智体 美劳全面发展方针,重视数学本质,突出理性思维、数学应用、数学探究、数学文化的引领作用. 1.以试题情境体现“核心价值引领”“核心素养立意” 高考评价体系的理念“核心价值引领”“核心素养立意”,是通过问题情境与情境活动两类载体来实 现的,即通过选取适宜的素材,再现学科理论产生的场景或是呈现现实中的问题情境,让学生在真 实的背景下发挥核心价值引领作用,运用必备知识和关键能力去解决实际问题,全面综合展现学 科素养水平. 真题再现 【例 1】(2020 山东,4)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面 的影子来测定时间.把地球看成一个球(球心记为 O),地球上一点 A 的纬度是指 OA 与地球赤道所 在平面所成角,点 A 处的水平面是指过点 A 且与 OA 垂直的平面.在点 A 处放置一个日晷,若晷面 与赤道所在平面平行,点 A 处的纬度为北纬 40°,则晷针与点 A 处的水平面所成的角为( ) A.20° B.40° C.50° D.90° 试题解读 此题以中国古代用来测定时间的仪器日晷和地球为问题情境,考查立体几何中直线与 平面所成角的概念及计算,此题既能够引导学生关注天文、地理等自然学科,又能引导学生了解 中国古代文明,激发学生爱国情怀. 【例 2】(2020 山东,6)基本再生数 R0 与世代间隔 T 是新冠肺炎的流行病学基本参数.基本再生数 指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初 始阶段,可以用指数模型:I(t)=er t 描述累计感染病例数 I(t)随时间 t(单位:天)的变化规律,指数增长 率 r 与 R0,T 近似满足 R0=1+rT.有学者基于已有数据估计出 R0=3.28,T=6.据此,在新冠肺炎疫情 初始阶段,累计感染病例数增加 1 倍需要的时间约为(ln 2≈0.69)( ) A.1.2 天 B.1.8 天 C.2.5 天 D.3.5 天 试题解读 此题以当前世界各国正在防控的重大疫情新冠肺炎的传染为问题情境,用数学模型揭 示病毒传播规律,贴近生活.让学生感受到数学源于生活,高于生活,服务于生活.在考查相关的数 学知识和从资料中提取信息的能力,突出数学知识和数学模型的应用的同时,通过计算累计感染 病例数增加 1 倍仅需要 1.8 天的结果,进一步引起学生重视自身的防护,感受中国在抗击疫情中 取得的重大成就,关注世界各国疫情防控的情况,从而坚定特色社会主义制度的优越性,树立起正 确的人生观、价值观. 【例 3】(2020 山东,7)已知 P 是边长为 2 的正六边形 ABCDEF 内的一点,则 �R� ���� ·��� ���� 的取值范围是 ( ) A.(-2,6) B.(-6,2) C.(-2,4) D.(-4,6) 试题解读 此题给考生以较大的想象空间,以及多样的选择性,虽然题干不长,条件不多,但考查了 “直观想象”“数学抽象”“数学运算”三大核心素养,以及数形结合的数学思想和建系求解的数学方 法. 【例 4】(2020 山东,12)信息熵是信息论中的一个重要概念.设随机变量 X 所有可能的取值为 1,2,…,n,且 P(X=i)=pi>0(i=1,2,…,n), ∑�=1 � pi=1,定义 X 的信息熵 H(X)=- ∑i=1 n pilog2pi.( ) A.若 n=1,则 H(X)=0 B.若 n=2,则 H(X)随着 p1 的增大而增大 C.若 pi= 1 � (i=1,2,…,n),则 H(X)随着 n 的增大而增大 D.若 n=2m,随机变量 Y 所有可能的取值为 1,2,…,m,且 P(Y=j)=pj+p2m+1-j(j=1,2,…,m),则 H(X)≤H(Y) 试题解读 此题以信息论中的重要概念信息熵为问题情境,结合中学所学的对数,分布列等知识编 制题目,考查学生获取新知识的能力和对新问题的理解探究能力,引导学生关注前沿科学. 【例 5】(2020 山东,15)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O 为圆孔 及轮廓圆弧 AB 所在圆的圆心,A 是圆弧 AB 与直线 AG 的切点,B 是圆弧 AB 与直线 BC 的切点,四 边形 DEFG 为矩形,BC⊥DG,垂足为 C,tan∠ODC= 3 5 ,BH∥DG,EF=12 cm,DE=2 cm,A 到直线 DE 和 EF 的距离均为 7 cm,圆孔半径为 1 cm,则图中阴影部分的面积为 cm2. 试题解读 此题以某中学开展劳动实习,学生加工制作零件为问题情境,给出了一个较为复杂的几 何图形,以及多个已知条件,考查学生处理复杂问题的逻辑思维的严密性,有序性,灵活性及解决实 际问题的能力,此题除对“逻辑推理”“数学运算”两大核心素养考查得比较深刻外,还充分体现了 高考命题对中学德智体美劳五育并举的引导. 【例 6】(2020 山东,19)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研, 随机抽查了 100 天空气中的 PM2.5 和 SO2 浓度(单位:μg/m3),得下表: SO2 PM2.5 [0,50](50,150](150,475] [0,35] 32 18 4 (35,75] 6 8 12 (75,115]3 7 10 (1)估计事件“该市一天空气中 PM2.5 浓度不超过 75,且 SO2 浓度不超过 150”的概率; (2)根据所给数据,完成下面的 2×2 列联表: SO2 PM2.5 [0,150](150,475] [0,75] (75,115] (3)根据(2)中的列联表,判断是否有 99%的把握认为该市一天空气中 PM2.5 浓度与 SO2 浓度有关? 试题解读 此题以加强环境保护,治理空气污染为问题情境,在重点考查学生概率统计知识,阅读理 解能力,“数据分析”“数学运算”两大核心素养的同时,还对引导学生增强环境保护的意识,提升科 学发展经济理念,对树立正确的人生观、价值观有积极的促进作用. 2.评价体系中的“四翼”考查要求在高考试题中的体现 (1)基础性要求的考查:创设基本层面的问题情境,要求学生调动单一的知识或技能解决问题.这种 考查方式与传统的考查方式基本上没有什么质的变化. 真题再现 【例 1】(2020 山东,1)设集合 A={x|1≤x≤3},B={x|2查看更多