2018届二轮复习专题5第1讲空间几何体的三视图、表面积及体积课件（61张）（全国通用）

2018届二轮复习专题5第1讲空间几何体的三视图、表面积及体积课件（61张）（全国通用）

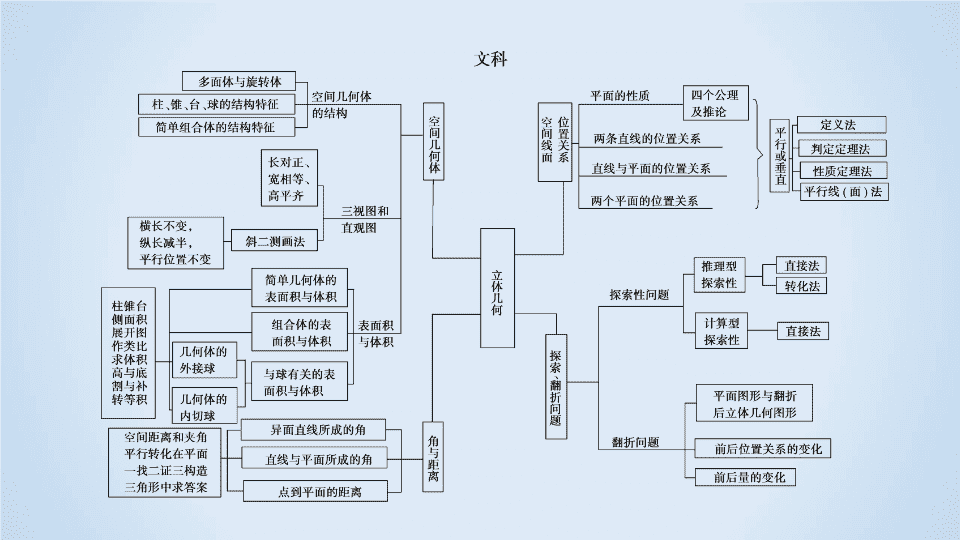
第一部分 专题强化突破 专题五　立体几何 知识网络构建 第一讲 　 空间几何体的三视图、表面积及体积 1 高考考点聚焦 2 核心知识整合 3 高考真题体验 4 命题热点突破 5 课后强化训练 高考考点聚焦 高考考点 考点解读 空间几何体的三视图与直观图的关系 1. 根据某几何体的部分三视图，判断该几何体的其他三视图；或者已知某几何体的三视图，判断该几何体的形状 2 ．考查三视图的画法以及数量关系 空间几何体的表面积与体积的计算 1. 以三视图为命题背景，考查空间几何体体积、表面积的计算方法 2 ．以空间几何体为命题背景考查空间几何体体积、表面积的计算方法 多面体与球的切、接问题 以球与多面体为背景，考查球的截面性质 备考策略 本部分内容在备考时应注意以下几个方面： (1) 加强对空间几何体结构特征的理解，掌握各种几何体的体积、表面积公式． (2) 掌握空间几何三视图的画法规则，掌握几何直观图中各个元素之间的关系以及三视图中长宽之间的关系． (3) 掌握球及球的截面的性质． 预测 2018 年命题热点为： (1) 已知空间几何体的三视图，求空间几何体的体积、表面积． (2) 已知空间几何体中各元素间的关系，求几何体的体积、表面积． (3) 给出球体与多面体，利用球的性质求解球的体积、表面积等． 核心知识整合 1 ． 柱体、锥体、台体、球的表面积与体积 Sh 　 2π rl ＋ 2π r 2 　 π rl ＋ π r 2 　 π( r ＋ r ′) l ＋ π r 2 ＋ π r ′ 2 　 4π R 2 　 2 ．空间几何体的三视图和直观图 (1) 空间几何体的三视图 三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形，三视图的画法规则为 “ 长对正、高平齐、宽相等 ”． 画三视图的基本要求：正 ( 主 ) 俯一样长，俯侧 ( 左 ) 一样宽，正 ( 主 ) 侧 ( 左 ) 一样高． 三视图排列规则：俯视图放在正 ( 主 ) 视图的下面；侧 ( 左 ) 视图放在正 ( 主 ) 视图的右面． (2) 空间几何体的直观图 空间几何体直观图的画法常采用斜二测画法．用斜二测画法画平面图形的直观图规则为 “ 轴夹角 45°( 或 135°) ，平行长不变，垂直长减半 ”． 1 ． 未注意三视图中实、虚线的区别 在画三视图时应注意看到的轮廓线画成实线，看不到的轮廓线画成虚线． 2 ． 不能准确分析组合体的结构致误 对简单组合体表面积与体积的计算要注意其构成几何体的面积、体积是和还是差． 3 ．台体可以看成是由锥体截得的，此时截面一定与底面平行． 4 ．空间几何放置的方式不同时，对三视图可能会有影响． 高考真题体验 A 　 B 　 D 　 B 　 B 　 A 　 36π 　 [ 解析 ] 　 如图，连接 OA ， OB ． 由 SA ＝ AC ， SB ＝ BC ， SC 为球 O 的直径，知 OA ⊥ SC ， OB ⊥ SC ． 命题热点突破 命题方向 1 　空间几何体的三视图 D 　 [ 分析 ] 　 根据三视图判断几何体为四棱锥，再利用体积公式求高 x 即可． D 　 [ 分析 ] 　 由已知中的四个三视图，可知四个三视图分别表示从前、后、左、右四个方向观察同一个棱锥，但其中有一个是错误的．根据 A 与 C 中俯视图正好旋转 180° ，故应是从相反方向进行观察，而其正视图和侧视图中三角形斜边倾斜方向相反，满足实际情况，可得 A ， C 均正确，而根据 A 和 C 可判断 B 正确， D 错误． [ 解析 ] 　 三棱锥的三视图均为三角形，四个选项均满足；且四个三视图均表示一个高为 3 ，底面为两直角边分别为 1,2 的棱锥； A 与 C 中俯视图正好旋转 180° ，故应是从相反方向进行观察，而其正视图和侧视图中三角形斜边倾斜方向相反，满足实际情况，故 A ， C 表示同一棱锥；设 A 中观察的正方向为标准正方向，所以 C 表示从后面观察该棱锥； B 与 D 中俯视图正好旋转 180° ，故应从相反方向进行观察，但侧视图中三角形斜边倾斜方向相同，不满足实际情况，故 B ， D 中有一个不与其他三个一样表示同一个棱锥，根据 B 中正视图与 A 中侧视图相同，侧视图与 C 中正视图相同，可判断 B 是从左边观察该棱锥．故选 D ． 『 规律总结 』 1 ． 由直观图确认三视图的方法 根据空间几何体三视图的定义及画法规则和摆放规则确认． 2 ． 由三视图还原到直观图的思路 (1) 根据俯视图确定几何体的底面． (2) 根据正视图或侧视图确定几何体的侧棱与侧面的特征，调整实线和虚线所对应的棱、面的位置． (3) 确定几何体的直观图形状． 提醒：在读图或者画空间几何体的三视图时，未注意三视图中的实虚线，造成对空间几何体的认识不准确或对三视图理解有差错 ． C 　 A ． (1)(2) 　 B ． (1)(3) 　 C ． (2)(4) 　 D ． (3)(4) 命题方向 2 　空间几何体的表面积与体积 B 　 『 规律总结 』 求几何体的表面积与体积问题，熟记公式是关键，应多角度全方位的考虑． 1 ． 给出几何体的形状、几何量求体积或表面积，直接套用公式． 2 ．用三视图给出几何体，先依据三视图规则想象几何体的形状特征，必要时画出直观图，找出其几何量代入相应公式计算． 3 ．用直观图给出几何体，先依据线、面位置关系的判定与性质定理讨论分析几何体的形状特征，再求体积或表面积． 4 ．求几何体的体积常用等积转化的方法，转换原则是其高易求，底面在几何体的某一面上，求不规则几何体的体积，主要用割补法． D 　 A 　 命题方向 3 　多面体与球 C 　 『 规律总结 』 多面体与球切、接问题的求解方法 (1) 涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点 ( 一般为接、切点 ) 或线作截面，把空间问题转化为平面问题求解． (2) 若球面上四点 P 、 A 、 B 、 C 构成的三条线段 PA 、 PB 、 PC 两两垂直，且 PA ＝ a ， PB ＝ b ， PC ＝ c ，一般把有关元素 “ 补形 ” 成为一个球内接长方体，根据 4 R 2 ＝ a 2 ＋ b 2 ＋ c 2 求解． (3) 正方体的内切球的直径为正方体的棱长． (4) 球和正方体的棱相切时，球的直径为正方体的面对角线长． (5) 利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径 ( 直径 ) 与该几何体已知量的关系，列方程 ( 组 ) 求解． A 　 B 　 课后强化训练