2019届二轮复习集合命题与不等式学案（全国通用）

2019届二轮复习集合命题与不等式学案（全国通用）

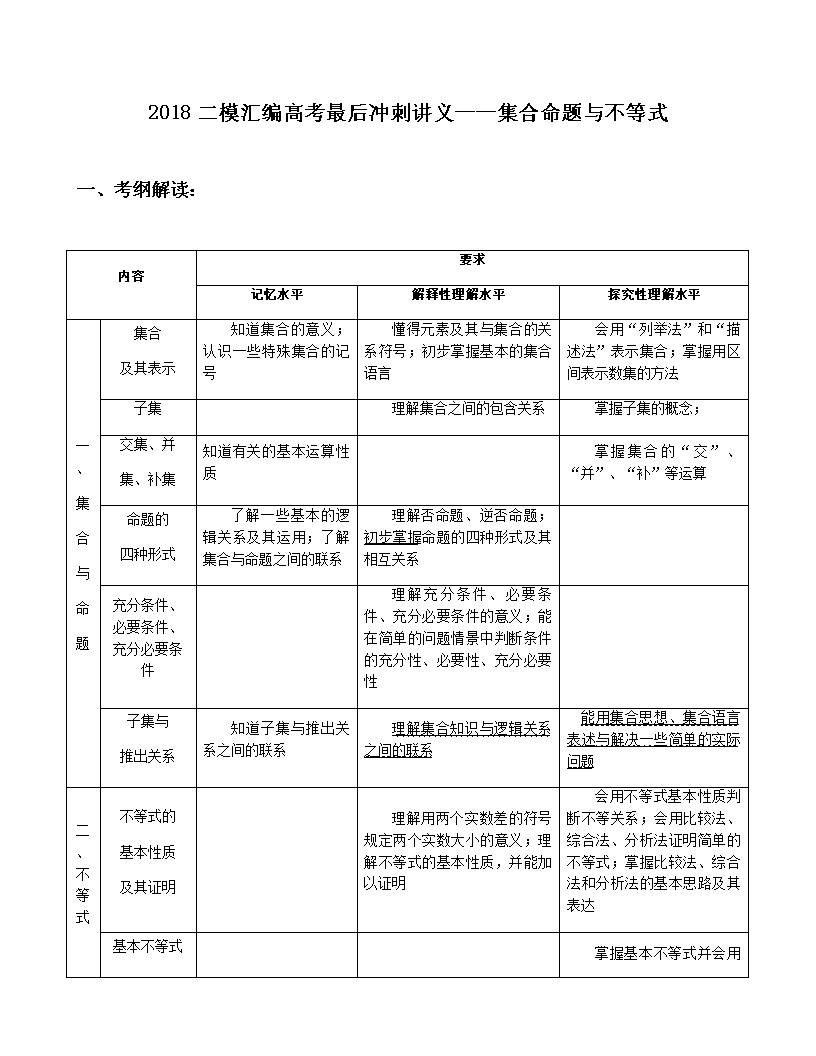
‎2018二模汇编高考最后冲刺讲义——集合命题与不等式 一、考纲解读：‎ 内容 要求 记忆水平 解释性理解水平 探究性理解水平 一、‎ 集 合 与 命 题 集合 及其表示 知道集合的意义；认识一些特殊集合的记号 懂得元素及其与集合的关系符号；初步掌握基本的集合语言 会用“列举法”和“描述法”表示集合；掌握用区间表示数集的方法 子集 ‎ 理解集合之间的包含关系 掌握子集的概念； ‎ 交集、并 集、补集 知道有关的基本运算性质 掌握集合的“交”、“并”、“补”等运算 命题的 四种形式 了解一些基本的逻辑关系及其运用；了解集合与命题之间的联系 理解否命题、逆否命题；初步掌握命题的四种形式及其相互关系 充分条件、必要条件、充分必要条件 理解充分条件、必要条件、充分必要条件的意义；能在简单的问题情景中判断条件的充分性、必要性、充分必要性 子集与 推出关系 知道子集与推出关系之间的联系 理解集合知识与逻辑关系之间的联系 ‎ 能用集合思想、集合语言表述与解决一些简单的实际问题 二、不等式 不等式的 基本性质 及其证明 理解用两个实数差的符号规定两个实数大小的意义；理解不等式的基本性质，并能加以证明 ‎ 会用不等式基本性质判断不等关系；会用比较法、综合法、分析法证明简单的不等式；掌握比较法、综合法和分析法的基本思路及其表达 基本不等式 掌握基本不等式并会用于解决简单的问题 一元二次 不等式（组）的解法 理解不等式、方程和函数之间的联系；初步会用不等式解决一些简单的实际问题； ‎ ‎ 掌握一元二次不等式的解法 分式不等式 的解法 ‎ 理解不等式、方程和函数之间的联系；初步会用不等式解决一些简单的实际问题。‎ ‎ 掌握分式不等式的解法 含有绝对值的不等式的解法 理解不等式、方程和函数之间的联系；初步会用不等式解决一些简单的实际问题；‎ 掌握可化为形如：或的绝对值不等式的解法，其中、、是一次多项式 二、知识梳理：‎ 1、 读懂描述法，关键是看竖线前面的字母或符合 ‎【例1】若P={y|y=x2,x∈R}，Q={(x，y)|y=x2,x∈R}，则必有（ ）‎ A．P∩Q=　 B．P Q C．P=Q D．P Q ‎【答案】A ‎【分析】有的同学一接触此题马上得到结论P=Q，这是由于他们仅仅看到两集合中的y=x2,x∈R相同，而没有注意到构成两个集合的元素是不同的，P集合是函数值域集合，Q集合是y=x2,x∈R上的点的集合，代表元素根本不是同一类事物．‎ 2、 ‎“子集”包含“真子集”“相等”两种情况；空集是任何子集的子集，任何非空集合的真子集。‎ ‎【例2】已知集合A={x|x2－3x－10≤0}，集合B={x|p＋1≤x≤2p－1}．若BA，则实数p的取值范围是________．‎ ‎【答案】p≤3．‎ ‎【分析】由x2－3x－10≤0得－2≤x≤5． ‎ 欲使BA，只须∴ p的取值范围是－3≤p≤3．‎ 上述解答忽略了"空集是任何集合的子集"这一结论，即B=时，符合题设．‎ 应有：①当B≠时，即p＋1≤2p－1p≥2．‎ 由BA得：－2≤p＋1且2p－1≤5．由－3≤p≤3．∴ 2≤p≤3.‎ ‎②当B=时，即p＋1>2p－1p＜2．‎ 由①、②得：p≤3．‎ 从以上解答应看到：解决有关A∩B=、A∪B=，AB等集合问题易忽视空集的情况而出现漏解，这需要在解题过程中要全方位、多角度审视问题．‎ 1、 通过画数轴或韦恩图求集合的运算 ‎【例3】设，，已知，，求、的值．‎ ‎【答案】，．‎ ‎【分析】如图所示，设想集合B所表示的范围在数轴上移动，‎ 显然当且仅当B覆盖住集合{x|－1－2}，且A∩B={x|1

查看更多