2019-2020学年江西省宜春市上高二中高二上学期第二次月考数学（文）试题（解析版）

2019-2020学年江西省宜春市上高二中高二上学期第二次月考数学（文）试题（解析版）

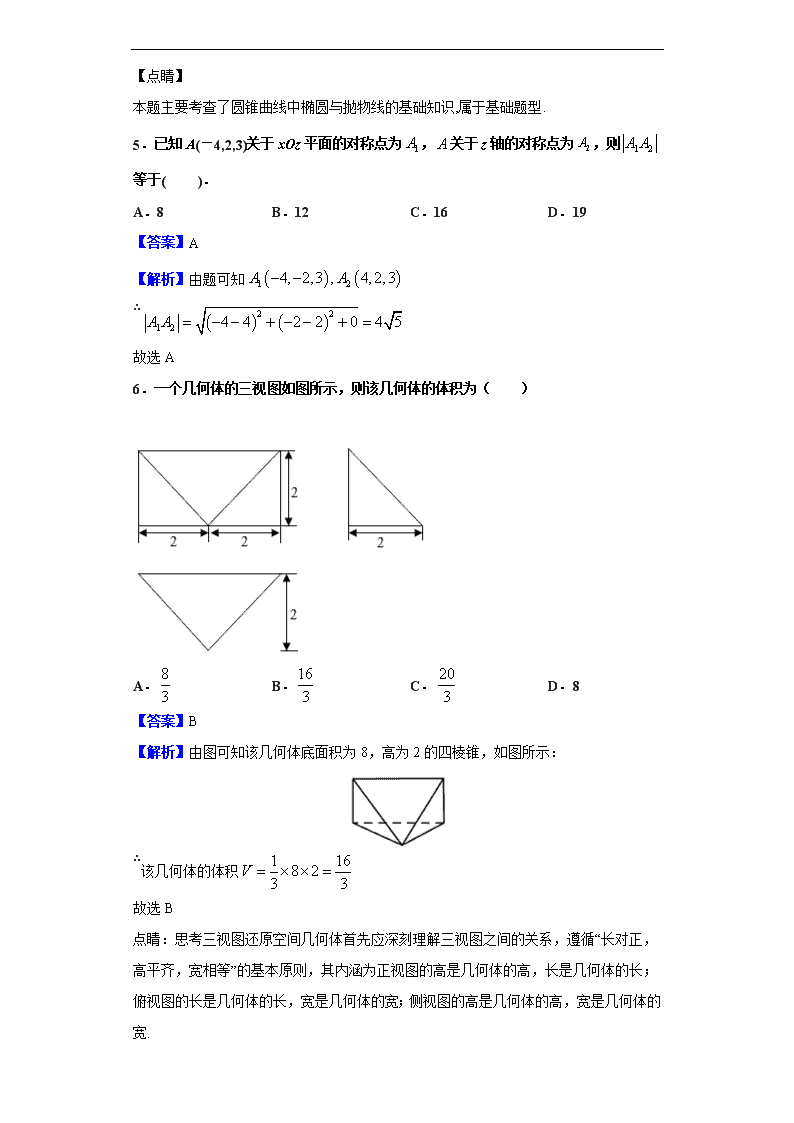
2019-2020 学年江西省宜春市上高二中高二上学期第二次月 考数学（文）试题 一、单选题 1．圆心坐标为 ，半径长为 2 的圆的标准方程是（） A． B． C． D． 【答案】C 【解析】根据圆的标准方程的形式写. 【详解】 圆心为 ，半径为 2 的圆的标准方程是 . 故选 C. 【点睛】 本题考查了圆的标准方程，故选 C. 2．已知抛物线的焦点坐标是（0，-3），则抛物线的标准方程为（ ） A． B． C． D． 【答案】A 【解析】根据焦点的坐标，确定抛物线的开口方向，同时求得 的值，进而求得抛物 线的方程. 【详解】 由于焦点坐标为 ，故焦点在 轴负半轴上，且 ，故抛物线方程 为 . 【点睛】 本小题主要考查已知抛物线的焦点坐标，求抛物线的方程，属于基础题. 3．已知水平放置的△ABC 是按“斜二测画法”得到如图所示的直观图，其中 B′O′＝C′O′ ＝1，A′O′＝ ，那么原△ABC 的面积是(　　) ( )1, 1− ( ) ( )2 21 1 2x y− + + = ( ) ( )2 21 1 2x y+ + − = ( ) ( )2 21 1 4x y− + + = ( ) ( )2 21 1 4x y+ + − = ( )1, 1− ( ) ( )2 21 1 4x y− + + = 2 12x y= − 2 12x y= 2 12y x= − 2 12y x= 2p ( )0, 3− y 3,2 122 p p= = 2 12x y= − 3 2 A． B．2 C． D． 【答案】A 【解析】先根据已知求出原△ABC 的高为 AO＝ ，再求原△ABC 的面积. 【详解】 由题图可知原△ABC 的高为 AO＝ ， ∴S△ABC＝ ×BC×OA＝ ×2× ＝ ，故答案为：A 【点睛】 本题主要考查斜二测画法的定义和三角形面积的计算，意在考察学生对这些知识的掌握 水平和分析推理能力. 4．椭圆 的一个焦点在抛物线 的准线上，则该椭圆的离心率为（ ） A． B． C． D． 【答案】B 【解析】先求出抛物线的焦点,再求得椭圆的焦点,进而算得离心率. 【详解】 解：由抛物线 的方程得准线方程为 , 又椭圆 的焦点为 ． ∵椭圆 的一个焦点在抛物线 的准线上,∴ ,得到 ． ∴ ,解得 ． ∴ ． 故选：B． 3 2 3 2 3 4 3 3 1 2 1 2 3 3 2 2 2 1x ya + = 2 4y x= 1 2 2 2 1 3 3 3 2 4y x= 1x = − 2 2 2 1x ya + = ( ),0c± 2 2 2 1x ya + = 2 4y x= 1c− = − 1c = 2 2 2 1 1 2a b c= + = + = 2a = 1 2 22 ce a = = = 【点睛】 本题主要考查了圆锥曲线中椭圆与抛物线的基础知识,属于基础题型. 5．已知 A(－4,2,3)关于 xOz 平面的对称点为 ， 关于 z 轴的对称点为 ，则 等于(　 　)． A．8 B．12 C．16 D．19 【答案】A 【解析】由题可知 ∴ 故选 A 6．一个几何体的三视图如图所示，则该几何体的体积为（　　） A． B． C． D．8 【答案】B 【解析】由图可知该几何体底面积为 8，高为 2 的四棱锥，如图所示： ∴该几何体的体积 故选 B 点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正， 高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长； 俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的 宽. 1A A 2A 1 2A A ( ) ( )1 24, 2,3 , 4,2,3A A− − ( ) ( )2 2 1 2 4 4 2 2 0 4 5A A = − − + − − + = 8 3 16 3 20 3 1 168 23 3V = × × = 7． 是椭圆 上一点， 、 分别是椭圆的左、右焦点，若 ，则 的大小为（　　） A． B． C． D． 【答案】B 【解析】根据椭圆的定义可判断 ，平方得出 ，再利 用余弦定理求解即可． 【详解】 是椭圆 上一点， 、 分别是椭圆的左、右焦点， ， ， ， ， 在 中， ， ， 故选 ． 【点睛】 本题考查了椭圆的定义，焦点三角形的问题，结合余弦定理整体求解是运算的技巧，属 于中档题． 8．如图所示，在正方体 中， ， 分别是 ， 的中点，则直线 与 所成角的余弦值是（ ） P 2 2 116 9 x y+ = 1F 2F 1 2 12PF PF = 1 2F PF∠ 30 60 120 150 1 2 8PF PF+ = 2 2 1 2 40PF PF+ = P 2 2 116 9 x y+ = 1F 2F 1 2 8PF PF∴ + = 1 2 2 7F F = 1 2 12PF PF⋅ = ( )2 1 2 64PF PF∴ + = 2 2 1 2 40PF PF∴ + = 1 2F PF∆ 1 2 40 28 1cos 2 12 2F PF −∠ = =× 1 2 60F PF∴∠ =  B 1AC E F 1DD BD 1AD EF A． B． C． D． 【答案】C 【解析】先通过平移将两条异面直线平移到同一个起点E，得到的锐角或直角就是异面 直线所成的角，在三角形中再利用余弦定理求出此角即可． 【详解】 如图，取 AD 的中点 G， 连接 EG，GF，∠GEF 为直线 AD1 与 EF 所成的角 设棱长为 2，则 EG= ，GF=1，EF= cos∠GEF= ， 故选：C． 【点睛】 本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力， 属于基础题． 9．已知 P 为抛物线 上的任意一点，记点 P 到 轴的距离为 ，对于给定点 ，则 的最小值为（ ） A． B． C． D． 【答案】B 【解析】根据抛物线的定义,画图分析转换 即可. 【详解】 解：抛物线 的焦点 ,准线 l：x＝﹣1． 如图所示,过点 P 作 交 y 轴于点 M,垂足为 N, 1 2 3 2 6 3 6 2 2 3 6 3 2 4y x= y d ( )4,5A PA d+ 34 34 1− 34 2− 34 4− PA d+ 2 4y x= ( )1,0F PN l⊥ 则 ,∴ ,∴ ． 故选：B． 【点睛】 本题主要考查了抛物线的定义,属于基础题型. 10．如图，过抛物线 的焦点 F 的直线交抛物线于点 A、B，交其准线 于点 C， 若 ，且 ，则 （ ） A．4 B．6 C．8 D．10 【答案】A 【解析】根据抛物线的定义转化 得 ,进而求得 即可. 【详解】 解：过 B 向准线做垂线垂足为 D,过 A 点做准线的垂线垂足为 E,准线与 x 轴交点为 G, 根据抛物线性质可知 ∵ ,∴ , ∴ , 又∵ , ∴ ∴ , PF PN= 1d PF= − ( )2 21 4 1 5 1 34 1PA d AF+ ≥ − = − + − = − 2 3y x= l 2BC BF= 3AF = AB = 2BC BF= 60EAC∠ = ° AB BD BF= 2BC BF= 2BC BD= 30C∠ = ° 60EAC∠ = ° AF AE= 60FEA∠ = ° 3AF AE CF= = = ∵ , , ∴ ． 故选：A． 【点睛】 本题主要考查了抛物线定义的运用,属于基础题型. 11．已知椭圆 的右焦点为 ，过点 的直线交椭圆 于 、 两点.若 的中点坐标为 ，则 的方程为（ ） A． B． C． D． 【答案】D 【解析】设 ，直线 的斜率 ， ，两式相减得 ，即 ，即 ， ，解得： ，方程是 ，故选 D. 12．如图，以等腰直角三角形 ABC 的斜边 BC 上的高 AD 为折痕，把△ABD 和△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论： ①BD⊥AC； ②△BAC 是等边三角形； 2 3CF GF= = 1BF = 4AB AF BF= + = 2 2 2 2: 1( 0)x yE a ba b + = > > ( )3,0F F E A B AB ( )1, 1− E 2 2 145 36 x y+ = 2 2 136 27 x y+ = 2 2 127 18 x y+ = 2 2 118 9 x y+ = ( ) ( )1 1 2 2, , ,A x y B x y AB 1 0 1 1 3 2k − −= =− 2 2 1 1 2 2 2 2 2 2 2 2 1 { 1 x y a b x y a b + = + = ( )( ) ( )( )1 2 1 2 1 2 1 2 2 2 0x x x x y y y y a b + − + −+ = ( )( ) ( )( )1 2 1 2 2 2 2 2 1 2 1 2 1 1 1 1 20 02 2 y y y y a b x x x x a b + −+ = ⇔ + × × =+ − − 2 22a b= 2 2 2 29,c a b c= = + 2 218, 9a b= = 2 2 118 9 x y+ = ③三棱锥 D－ABC 是正三棱锥； ④平面 ADC⊥平面 ABC． 其中正确的是（ ） A．①②④ B．①②③ C．②③④ D．①③④ 【答案】B 【解析】根据翻折后垂直关系得BD⊥平面 ADC，即得 BD⊥AC，再根据计算得△BAC 是 等边三角形，最后可确定选项. 【详解】 由题意知，BD⊥平面 ADC，故 BD⊥AC，①正确；AD 为等腰直角三角形斜边 BC 上的 高，平面 ABD⊥平面 ACD，所以 AB＝AC＝BC，△BAC 是等边三角形，②正确；易知 DA ＝DB＝DC，又由②知③正确；由①知④错． 故选：B. 【点睛】 本题考查线面垂直判定与性质，考查推理论证求解能力，属中档题. 二、填空题 13．直线 与焦点在 轴上的椭圆 总有公共点，则实数 的取值 范围为______． 【答案】 【解析】根据直线 恒过定点 ,再判断 与椭圆的位置关系列不等 式即可. 【详解】 解：直线 恒过定点 , 焦点在 x 轴上的椭圆 ,可得 ,① 由直线 与焦点在 x 轴上的椭圆 总有公共点,可得 P 在椭圆上或椭 圆内, 1y kx= + x 2 2 19 x y m + = m [ )1,9 1y kx= + ( )0,1P ( )0,1P 1y kx= + ( )0,1P 2 2 19 x y m + = 0 9m< < 1y kx= + 2 2 19 x y m + = 即有 ,解得 ,② 由①②可得 ． 故答案为： ． 【点睛】 本题主要考查了直线与椭圆的位置关系,需要根据直线的定点来分析,属于基础题型. 14．过点 的直线将圆形区域 分为两部分，使得这两部分的面 积之差最大，则该直线的方程为________________． 【答案】x＋y－2＝0 【解析】当 OP 与所求直线垂直时面积之差最大，故所求直线方程为 x＋y－2＝0. 15．在平面直角坐标系 xOy 中，已知椭圆 (a＞b＞0) 的左、右焦点分别为 F1，F2，过 F1 且与 x 轴垂直的直线交椭圆于 A，B 两点，直线 AF2 与椭圆的另一个交 点为 C．若 ，则该椭圆的离心率为______． 【答案】 【解析】 由题意, ， ∵ ,∴ , . ∴ 代入椭圆 (a>b>0)， 得 ,即 解得 . 故答案为： . 16．已知三棱锥 内接于球 ， ，当三棱锥 的三 0 1 19 m + ≤ m 1≥ 1 9m≤ < [ )1,9 (1,1)P 2 2{( ) 4|, }x y x y+ ≤ 2 2 2 2 1x y a b + = 2 22AF F C=  5 5 2 , bA c a  − −   2 22AF F C=  2 2C by a = 2Cx c= 2 2 , ,2 bC c a      2 2 2 2 1x y a b + = 2 2 2 2 4 14 c b a a + = 2 25c a= 5 5e = 5 5 P ABC− O 2PA PB PC= = = P ABC− 个侧面的面积之和最大时，球 的表面积为__________． 【答案】 【解析】由于三条侧棱相等，根据三角形面积公式可知，当 两两垂直时， 侧面积之和最大.此时 可看成正方体一个顶点的三条侧棱，其外接球直径为 正方体的体对角线，即 ，故球的表面积为 . 三、解答题 17．已知圆心为 C 的圆经过点 和 ，且圆心在直线 上 （1）求圆 C 的标准方程； （2）若直线 被圆 C 截得的弦长为 8，求 的取值． 【答案】（1） （2） 【解析】(1)根据圆心在弦的中垂线上可求得圆心与半径. (2)先求得圆心到直线的距离再利用垂径定理求解即可. 【详解】 解：∵点 和 , ∴ ,线段 AB 的中点坐标为 , ∴线段 AB 垂直平分线方程为 ,即 , 与直线 联立得： , 解得： , ∴圆心 C 坐标为 , ∴半径 , 则圆 C 方程为 ； （2）∵圆 C 半径为 5,弦长为 8, ∴圆心到直线 的距离 ,即 , O 12π , ,PA PB PC , ,PA PB PC 2 24 3 2 12R = ⋅ = 24π 12πR = ( )1,1A − ( )2, 2B − − : 1 0l x y+ − = 5 0kx y− + = k ( ) ( )2 23 2 25x y− + + = 20 21k = − ( )1,1A − ( )2, 2B − − AB 2 1 32 1k − −= =− +直线 3 1,2 2  − −   1 1 3 2 3 2y x + = − +   3 3 0x y+ + = l 1 0 3 3 0 x y x y + − =  + + = 3 2 x y =  = − ( )3, 2− ( ) ( )2 21 3 1 2 5AC = − − + + = ( ) ( )2 23 2 25x y− + + = 5 0kx y− + = 2 25 4 3d = − = 2 3 7 3 1 k k + = + 解得： ． 【点睛】 本题主要考查了直线与圆相交的垂径定理运用,属于中等题型. 18．如图，四棱锥 A﹣BCDE 中， 是正三角形，四边形 BCDE 是矩形，且平面 ABC⊥平面 BCDE， ， ． （1）若点 G 是 AE 的中点，求证： 平面 BDG （2）若 F 是线段 AB 的中点，求三棱锥 B﹣EFC 的体积． 【答案】（1）证明见解析（2） 【解析】(1) 设 ,连接 OG,再证 即可. (2)利用换顶点得 求解即可. 【详解】 解：如图, （1）证明：设 ,连接 OG, 由三角形的中位线定理可得： , ∵ 平面 , 平面 ,∴ 平面 ． （2）∵平面 平面 , , ∴ 平面 ,∴ ,∴ ； 又∵F 是 AB 的中点, 是正三角形, ∴ , ∴ , 又平面 平面 , , ∴ 平面 , ∴ ． 20 21k = − ABC∆ 2AB = 4=AD AC  1 CE BD O= OG AC B EFC E BCFV V− −= CE BD O= OG AC AC ⊄ BDG OG ⊂ BDG AC  BDG ABC ⊥ BCDE DC BC⊥ DC ⊥ ABC DC AC⊥ 2 2 2 3DC AD AC= − = ABC∆ CF AB⊥ 1 3 2 2BCFS BF CF∆ = ⋅ = ABC ⊥ BCDE EB BC⊥ EB ⊥ BCF 1 13B EFC E BCF BCFV V S EB− − ∆= = ⋅ = 【点睛】 本题主要考查了线面平行的证明与换顶点求体积的方法,属于中等题型. 19．已知抛物线 的焦点与椭圆 的右焦点重合，抛物线 的顶点在坐 标原点，过点 的直线 与抛物线 分别相交于 两点. （1）写出抛物线 的标准方程； （2）求 面积的最小值. 【答案】(1) ；(2)16. 【解析】试题分析：（1）椭圆 的右焦点为 即为抛物线 的焦点， 2 分 得抛物线的标准方程为 5 分 （2）当直线 AB 的斜率不存在时，直线方程为 ，此时 ，⊿ABO 的面积 = 7 分 当直线 AB 的斜率存在时，设 AB 的方程为 （ ）联立 消去 ，有 ， ， 9 分 设 A（ ）B（ ） 有 ， 11 分 ∴ = 综上所述，面积最小值为 16 13 分 1C 2 2 2 : 16 5 x yC + = 1C ( )4,0M l 1C ,A B 1C ABO∆ 2 4y x= 2 2 2 : 16 5 x yC + = ( )1,0 1C 2 4y x= 4x = 8AB = S 1 8 4 162 × × = ( )4y k x= − 0k ≠ ( ) 2 4{ 4 y k x y x = − = x 2 4 16 0ky y k− − = 216 64 0k∆ = + > 1 1,x y 2 2,x y 1 2 4y y k + = 1 2• 16y y = − 1 2 1 2AOB AOM BOMS S S OM y y= + = − 2 162 64 16k + > 【考点】椭圆抛物线方程性质及直线与圆锥曲线的位置关系 点 评 ： 抛 物 线 焦 点 为 ， 椭 圆 焦 点 为 其 中 当直线与圆锥曲线相交时，常联立方程借助于方程根与系数的关系求解 20．如图，三棱柱 的侧面 是矩形，侧面 ⊥侧面 ， 且 ， ， 是 的中点． （1）求证： ∥平面 ； （2）求证： ⊥平面 ． 【答案】（1）见解析；（2）见解析 【解析】（1）连结 交 于 ，取 中点 ，连结 ， ．通过证明四边 形 是平行四边形，来证得 ，从而证得 平面 .（2）利用 余弦定理和勾股定理，计算证明证得 ；利用面面垂直的性质定理，证得 ；从而证得 平面 . 【详解】 证明：（1）连结 交 于 ，取 中点 ，连结 ， ． ∵四边形 是矩形，∴ 是 的中点， ∴ ， ， ∵四边形 是平行四边形， 是 的中点， ∴ ， ， ∴四边形 是平行四边形，∴ ，即 ． 又∵ ， ， ∴ ∥平面 ． 2 2y px= ,02 p     2 2 2 2 1x y a b + = ( ),0c± 2 2 2a b c= + 1 1 1ABC A B C− 1 1AAC C 1 1AAC C 1 1AA B B 14 4AB AA= = 1 60BAA∠ = ° D AB 1AC 1CDB 1DA 1 1AAC C 1AC 1AC F 1B C E DE EF ADEF 1 / /AC DE 1 / /AC 1CDB 1 1A D AA⊥ 1A D AC⊥ 1DA ⊥ 1 1AAC C 1AC 1AC F 1B C E DE EF 1 1AAC C F 1AC 1 1//EF A B 1 1 1 2EF A B= 1 1ABB A D AB 1 1//AD A B 1 1 1 2AD A B= ADEF //AF DE 1 //AC DE 1DE CDB⊂ 平面 1 1AC CDB⊄ 平面 1AC 1CDB （2）∵ ， 是 中点，∴ ， ， ∵ ，∴ ． ∴ ，∴ ， ∵侧面 ⊥侧面 ，侧面 ∩侧面 = ， ， ⊂ 平面 ， ∴ ⊥平面 ，∵ ⊂平面 ， ∴ ⊥ ，又∵ ⊂平面 ， ⊂平面 ， ， ∴ ⊥平面 ． 【点睛】 本小题主要考查线面平行的证明，考查线面垂直的证明，还考查了面面垂直的性质定理 的应用，属于中档题. 21．如图 1，在矩形 ABCD 中，AB＝4，AD＝2，E 是 CD 的中点，将△ADE 沿 AE 折 起，得到如图 2 所示的四棱锥 D1—ABCE，其中平面 D1AE⊥平面 ABCE. (1)证明：BE⊥平面 D1AE； (2)设 F 为 CD1 的中点，在线段 AB 上是否存在一点 M，使得 MF∥平面 D1AE，若存在， 求出 的值；若不存在，请说明理由． 【答案】（1）证明见解析（2）线段 AB 上存在满足题意的点 M，且 ＝ 【解析】（1）先计算得 BE⊥AE，再根据面面垂直性质定理得结果，（2）先分析确定点 M 位置，再取 D1E 的中点 L，根据平几知识得 AMFL 为平行四边形，最后根据线面平行 判定定理得结果. 【详解】 14 4AB AA= = D AB 1 1AA = 2AD = 1 60BAA∠ = ° 2 2 1 1 12 cos60 3A D AD AA AD AA= + − ⋅ ° = 2 2 2 1 1AA A D AD+ = 1 1A D AA⊥ 1 1AAC C 1 1AA B B 1 1AAC C 1 1AA B B 1AA 1AC AA⊥ AC 1 1AAC C AC 1 1AA B B 1A D 1 1AA B B AC 1A D 1AA 1 1AAC C AC 1 1AAC C 1AC AA A∩ = 1DA 1 1AAC C AM AB AM AB 1 4 (1)证明连接 BE， ∵ABCD 为矩形且 AD＝DE＝EC＝BC＝2， ∴∠AEB＝90°，即 BE⊥AE， 又平面 D1AE⊥平面 ABCE， 平面 D1AE∩平面 ABCE＝AE，BE⊂平面 ABCE， ∴BE⊥平面 D1AE. (2)解 AM＝ AB，取 D1E 的中点 L，连接 AL，FL， ∵FL∥EC，EC∥AB，∴FL∥AB 且 FL＝ AB， ∴FL∥AM，FL=AM ∴AMFL 为平行四边形，∴MF∥AL， 因为 MF 不在平面 AD1E 上， AL⊂平面 AD1E，所以 MF∥平面 AD1E. 故线段 AB 上存在满足题意的点 M，且 ＝ . 【点睛】 本题考查线面平行判定定理以及面面垂直性质定理，考查基本分析论证求解能力，属中 档题. 22．已知椭圆 ( )的短轴长为 2，离心率为 ．过点 M（2,0） 的直线 与椭圆 相交于 、 两点, 为坐标原点. （1）求椭圆 的方程； （2）求 的取值范围； （3）若 点关于 轴的对称点是 ，证明：直线 恒过一定点. 【答案】（1） .（2） .（3）直线 过定点 . 【解析】试题分析：（1）由已知得 ,得 . 1 4 1 4 AM AB 1 4 2 2 2 2: 1x yC a b + = 0a b> > 2 2 l C A B O C OA OB⋅  B x N AN 2 2 12 x y+ = 3[ 2, )2 − l (1,0) 2 2 2 22 2 2a c a b= = − 2 2a = （2）设 ： ，与椭圆 的方程联立,消去 得 .由△＞0 得 . 设 ,则 . 将 表示成为 由 ，求得范围是 . （3）由对称性可知 N ，定点在 轴上. 在直线方程 AN： 中，令 得: ,得证. 试题解析：（1）易知 ， 得 ,故 . 故方程为 .（3 分） （2）设 ： ，与椭圆 的方程联立,消去 得 .由△＞0 得 . 设 ,则 . ∴ = ，∴ ， 故所求范围是 .（8 分） （3）由对称性可知 N ，定点在 轴上. l ( 2)y k x= − C y 2 2 2 2(1 2 ) 8 8 2 0k x k x k+ − + − = 2 10 2k≤ < 1 1 2 2( , ), ( , )A x y B x y 2 2 1 2 1 22 2 8 8 2,1 2 1 2 k kx x x xk k −+ = =+ + 1 2 1 2OA OB x x y y⋅ = +  2 2 2 10 2 751 2 1 2 k k k − = −+ + 2 10 2k≤ < 3[ 2, )2 − 2 2( , )x y− x 1 2 1 1 1 2 ( )y yy y x xx x +− = −− 0y = 2 2 2 21 1 2 1 2 2 1 1 2 1 2 1 2 1 2 1 2 1 2 2 16 4 16 ( ) 2 2( ) 1 2 1 2 184 41 2 k k y x x x y x y x x x x k kx x ky y y y x x k − −− + − + + += − = = = =+ + + − −+ 1b = 2 2 ce a = = 2 2 2 22 2 2a c a b= = − 2 2a = 2 2 12 x y+ = l ( 2)y k x= − C y 2 2 2 2(1 2 ) 8 8 2 0k x k x k+ − + − = 2 10 2k≤ < 1 1 2 2( , ), ( , )A x y B x y 2 2 1 2 1 22 2 8 8 2,1 2 1 2 k kx x x xk k −+ = =+ + 1 2 1 2OA OB x x y y⋅ = +  2 2 2 2 1 2 1 2 1 2 1 2( 2)( 2) (1 ) 2 ( ) 4x x k x x k x x k x x k= + − − = + − + + 2 2 2 10 2 751 2 1 2 k k k − = −+ + 2 10 2k≤ < 2 7 7 72 1 2k < ≤+ 3[ 2, )2 − 2 2( , )x y− x 直线 AN： ，令 得: , ∴直线 过定点 .（13 分） 【考点】椭圆的几何性质，直线与圆锥曲线的位置关系，平面向量的坐标运算. 1 2 1 1 1 2 ( )y yy y x xx x +− = −− 0y = 2 2 2 21 1 2 1 2 2 1 1 2 1 2 1 2 1 2 1 2 1 2 2 16 4 16 ( ) 2 2( ) 1 2 1 2 184 41 2 k k y x x x y x y x x x x k kx x ky y y y x x k − −− + − + + += − = = = =+ + + − −+ l (1,0)