数学卷·2019届云南省德宏州梁河县第一中学高二上学期第一次月考（2017-09）

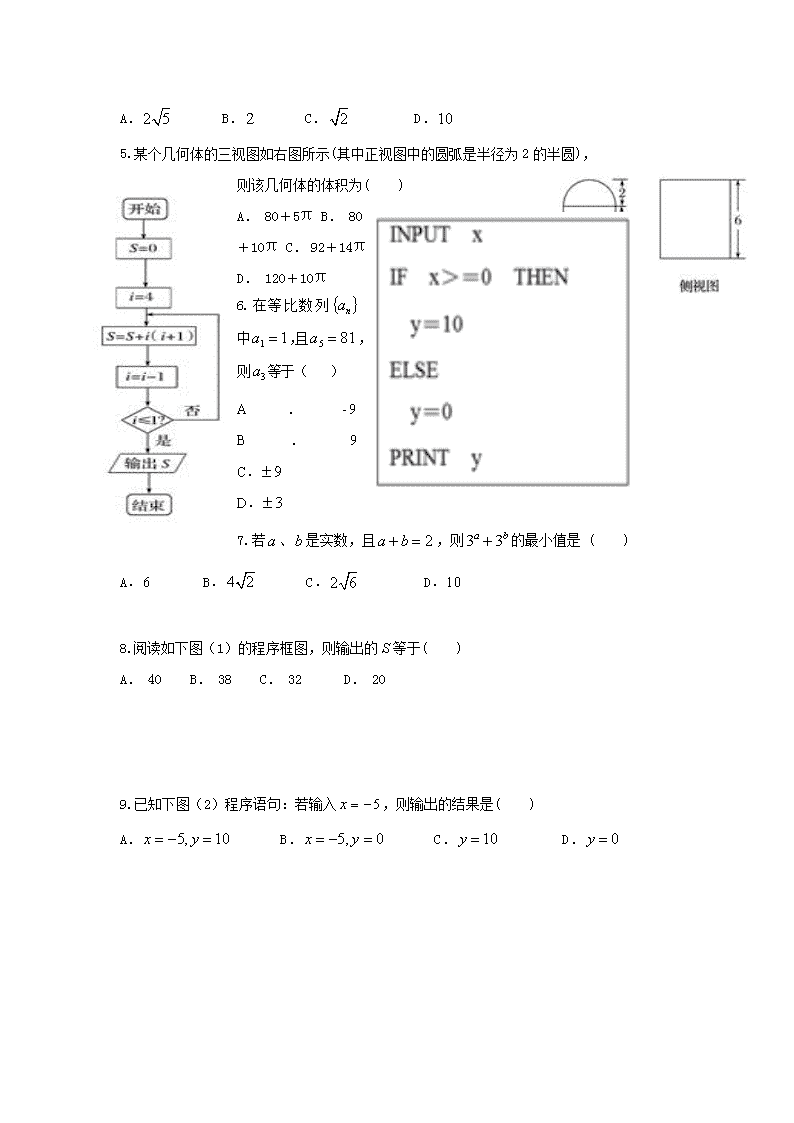
数学卷·2019届云南省德宏州梁河县第一中学高二上学期第一次月考（2017-09）

‎ 梁河县第一中学2017-2018学年上学期第一次月考 ‎ 高二年级数学试卷 ‎ 出卷人：孙冠男 审卷人：张自石 注意：‎ ‎1、本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试时间120分钟，满分150分.‎ ‎2、答题前，考生务必将自己的相关信息填写在答题卡上.‎ ‎3、答卷时，必须使用黑色墨水签字笔在答题卡上书写，要求字体工整、笔迹清晰。作图题可先用铅笔在答题卡规定的位置绘出，确认后再用黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效.‎ ‎4、考试结束，监考员只将答题卡分开收回，试题卷由考生自己保管. ‎ 第Ⅰ卷 一. 选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）. ‎ ‎1.若集合,，则(　　)‎ A． B． C． D．‎ ‎2.的值 （ ）‎ A． B． C． D．‎ ‎3.要得到的图像，只需将的图像 (　　)‎ A．向右平移个单位 B．向左平移个单位C．向右平移个单位D．向左平移个单位　‎ ‎4.若，，则向量在向量方向上的投影为 (　　)‎ A． B． C． D．‎ ‎5.某个几何体的三视图如右图所示(其中正视图中的圆弧是半径为2的半圆)，‎ 则该几何体的体积为(　　)‎ A． 80＋5π B． 80＋10π C． 92＋14π D． 120＋10π ‎6.在等比数列中，且，则等于（ ） ‎ A． B． C． D．‎ ‎7.若、是实数，且，则的最小值是 (　　)‎ A． B． C． D．‎ ‎8.阅读如下图（1）的程序框图，则输出的等于(　　)‎ A． 40 B． 38 C． 32 D． 20‎ 9. 已知下图（2）程序语句：若输入，则输出的结果是(　　)‎ A． B． C． D．‎ ‎ ‎ ‎ ‎ ‎ 图（1） 图（2） ‎ 9. 设，，，则(　　)‎ A． ‎ B． C． D．‎ ‎11.和的最大公约数是(　　)‎ A． 51 B． 17 C． 9 D． 3‎ ‎12.圆与的位置关系为(　　)‎ A． 两圆相内切 B． 两圆相外切 C． 两圆相交 D． 两圆相离 第Ⅱ卷 一. 填空题（本大题共4小题，每小题5分，共20分）.‎ ‎13.设实数满足约束条件 ，若，则的最小值是_____．‎ ‎14.________．‎ ‎15.已知，则的值为________．‎ ‎16.将二进制数化为八进制数，结果为________．‎ 三．解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）. ‎ ‎17.(10分)截至2016年底，已知某市人口数为80万，若今后能将人口年平均增长率控制在1%，‎ 经过x年后，此市人口数为y(万)．‎ ‎(1)求y与x的函数关系y＝f(x)，并求函数的定义域；‎ ‎(2)判断函数的单调性．‎ ‎18.（12）在等比数列中，是和的等差中项． ‎ ‎（1）求数列的通项公式； ‎ ‎（2）记，求数列的前项和． ‎ ‎19.(12分）已知锐角△ABC的三内角所对的边分别是，且． ‎ ‎（1）求角的大小；‎ ‎（2）若,求边的长． ‎ ‎ ‎ ‎20.(12分）如图，正方体的棱长为2. ‎ ‎（1）求证：；（2）求三棱锥的体积.‎ ‎21.(12分）已知圆心为的圆经过点. ‎ ‎（1）求圆的标准方程；‎ ‎（2）若直线过点且被圆截得的线段长为,求直线的方程.‎ ‎22.(12分）已知函数的一段图象如图所示. ‎ (1) 求f(x)的解析式； ‎ ‎(2)求f(x)的单调减区间，并指出f(x)的最大值及取到最大值时x的集合..‎ 答案解析 一 、选择题 ADCBB BABD AC 二、填空题 ‎13.　-2 14.7 15. 16.55(8)‎ ‎17.(1)由题设条件知，经过x年后此市人口总数为80(1＋1%)x(万)，‎ ‎∴y＝f(x)＝80(1＋1%)x.‎ ‎∵此问题以年作为单位时间，∴此函数的定义域是N*.‎ ‎(2)y＝f(x)＝80(1＋1%)x是指数型函数，‎ ‎∵1＋1%>1，∴y＝80(1＋1%)x是增函数．‎ ‎18.(1)设数列{an}的公比为q，‎ 由题意知： 2(a3＋2)＝a2＋a4，‎ ‎∴q3－2q2＋q－2＝0，即(q－2)(q2＋1)＝0.‎ ‎∴q＝2，即an＝2·2n－1＝2n.‎ ‎(2)bn＝n·2n，‎ ‎∴Sn＝1·2＋2·22＋3·23＋…＋n·2n.①‎ ‎2Sn＝1·22＋2·23＋3·24＋…＋(n－1)·2n＋n·2n＋1.②‎ ‎①－②得－Sn＝21＋22＋23＋24＋…＋2n－n·2n＋1‎ ‎＝－2－(n－1)·2n＋1.‎ ‎∴Sn＝2＋(n－1)·2n＋1.‎ ‎19.解　(1)由正弦定理，得2sinCsinA＝sinA，又sinA≠0，‎ ‎∴sinC＝，又△ABC是锐角三角形，∴C＝.‎ ‎(2)由S△ABC＝absinC，得b＝6,‎ 由c2＝a2＋b2－2abcosC，得c＝，‎ ‎20：(1)证明：为正方体 面，且底面为正方形 面 (2) ‎21.(1)圆C的半径为|CM|＝＝4，‎ ‎∴圆C的标准方程为(x＋2)2＋(y－6)2＝16.‎ ‎(2)方法一　如图所示，设直线l与圆C交于A，B两点且D是AB的中点，则|AB|＝4，|AD|＝2且CD⊥AB.‎ ‎∵圆C的半径为4，即|AC|＝4，‎ ‎∴在Rt△ACD中，可得|CD|＝＝2，‎ 即点C到直线l的距离为2.‎ ‎(i)当所求直线l的斜率存在时，设所求直线的方程为y＝kx＋5，即kx－y＋5＝0.‎ 由点到直线的距离公式得＝2，‎ 解得 ‎∴此时直线l的方程为3x－4y＋20＝0.‎ ‎(ii)当直线l的斜率不存在时，直线l的方程为x＝0.‎ 将x＝0代入(x＋2)2＋(y－6)2＝16，得(y－6)2＝16－4＝12，y－6＝±2，‎ ‎∴y1＝6＋2，y2＝6－2，|y1－y2|＝4，‎ ‎∴方程为x＝0的直线也满足题意，‎ ‎∴所求直线l的方程为3x－4y＋20＝0或x＝0.‎ 方法二　当所求直线l的斜率存在时，设所求直线的方程为y＝kx＋5，即kx－y＋5＝0.‎ 联立直线与圆C的方程 消去y得(1＋k2)x2＋(4－2k)x－11＝0，①‎ 设方程①的两根为x1，x2，‎ 由根与系数的关系得②‎ 由弦长公式得|x1－x2|＝‎ ＝4，③‎ 将②式代入③，并解得，‎ 此时直线l的方程为3x－4y＋20＝0.‎ 当直线l的斜率不存在时，直线l的方程为x＝0，‎ 仿方法一验算得方程为x＝0的直线也满足题意．‎ ‎∴所求直线l的方程为3x－4y＋20＝0或x＝0.‎ ‎22.(1)由图象可以得到函数f(x)的振幅A＝3，‎ 设函数周期为T，则T＝4π－＝，‎ 所以T＝5π，则ω＝，‎ 由ωx0＋φ＝0，得×＋φ＝0，所以φ＝－，‎ 所以f(x)＝3sin(x－).‎ ‎(2)由＋2kπ≤x－≤＋2kπ()，　‎ 得＋5kπ≤x≤4π＋5kπ()，‎ 所以函数的减区间为(＋5kπ，4π＋5kπ)，.‎ 函数f(x)的最大值为3，当且仅当x－＝＋2kπ，，即x＝＋5kπ()时函数取得最大值.‎ 所以函数的最大值为3，取得最大值时的x的集合为{x|x＝＋5kπ()}.‎