高考数学【理科】真题分类详细解析版专题7 平面向量（原卷版）

高考数学【理科】真题分类详细解析版专题7 平面向量（原卷版）

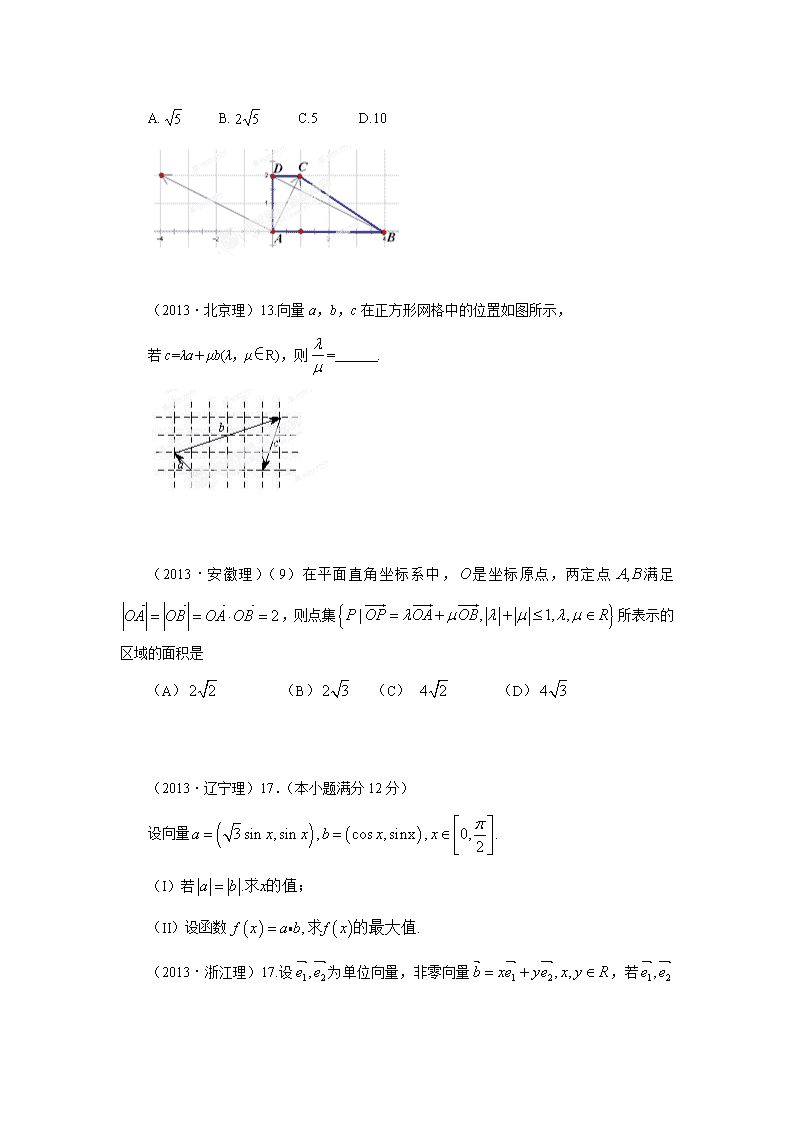
专题07 平面向量 ‎【2013高考真题】‎ ‎（2013·新课标I理）（13）已知两个单位向量，的夹角为，，若，则_____。‎ ‎（2013·新课标Ⅱ理）（13）已知正方形ABCD的边长为2，E为CD的中点，则 =_______.‎ ‎（2013·浙江理）7.设是边上一定点，满足，且对于边上任一点，恒有,则（ ）‎ A. B. C. D.‎ ‎（2013·天津理）12. 在平行四边形ABCD中, AD = 1, , E为CD的中点. ‎ 若, 则AB的长为 .‎ ‎（2013·上海理）18．在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为；以D为起点，其余顶点为终点的向量分别为.若分别为的最小值、最大值，其中,,则满足（ ）. ‎ ‎(A) (B) ‎ ‎ (C) (D) ‎ ‎（2013·陕西理）3. 设a, b为向量, 则“”是“a//b”的 （ ）‎ ‎ (A) 充分不必要条件 (B) 必要不充分条件 ‎ (C) 充分必要条件 (D) 既不充分也不必要条件 ‎（2013·山东理）15.已知向量与的夹角为，且 若，且，则实数的值为_____.‎ ‎（2013·辽宁理）（3）已知点 ‎（A） （B） （C） （D）‎ ‎（2013·江西理）12．设e1，e2为单位向量。且e1、e2的夹角为 ，若a=e1+3e2，b=2e1，则向量a在b方向上的射影为________.‎ ‎ （2013·湖南理）6. 已知是单位向量，.若向量满足（ ）‎ A． B． ‎ C． D． ‎ ‎7. 在四边形中，，,则该四边形的面积为（ ）‎ A. B. C.5 D.10 ‎ ‎（2013·北京理）13.向量a，b，c在正方形网格中的位置如图所示，‎ 若c=λa＋μb(λ，μ∈R)，则= .‎ ‎（2013·安徽理）（9）在平面直角坐标系中，是坐标原点，两定点满足，则点集所表示的区域的面积是 ‎（A） （B） （C） （D）‎ ‎（2013·辽宁理）17．（本小题满分12分）‎ 设向量 ‎（I）若 ‎（II）设函数 ‎（2013·浙江理）17.设为单位向量，非零向量，若 的夹角为，则的最大值等于________。‎ ‎【2012高考真题】‎ ‎1．（2012·浙江卷设a，b是两个非零向量(　　)‎ A．若|a＋b|＝|a|－|b|，则a⊥b B．若a⊥b，则|a＋b|＝|a|－|b|‎ C．若|a＋b|＝|a|－|b|，则存在实数λ，使得b＝λa D．若存在实数λ，使得b＝λa，则|a＋b|＝|a|－|b|‎ ‎2．（2012·陕西卷） 已知椭圆C1：＋y2＝1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．‎ ‎(1)求椭圆C2的方程；‎ ‎(2)设O为坐标原点，点A，B分别在椭圆C1和C2上，＝2，求直线AB的方程．‎ ‎3．（2012·广东卷） 若向量＝(2,3)，＝(4,7)，则＝(　　)‎ A．(－2，－4) B．(2,4)‎ C．(6,10) D．(－6，－10)‎ ‎4．（2012·全国卷） △ABC中，AB边的高为CD，若＝a，＝b，a·b＝0，|a|＝1，|b|＝2，则＝(　　)‎ ‎5．（2012·安徽卷） 在平面直角坐标系中，点O(0,0)，P(6,8)，将向量绕点O 按逆时针方向旋转后得向量，则点Q的坐标是(　　)‎ A．(－7，－) B．(－7，)‎ C．(－4，－2) D．(－4，2)‎ ‎6．（2012·江西卷） 在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则＝(　　)‎ A．2 B．‎4 C．5 D．10‎ ‎7．（2012·重庆卷） 设x，y∈R，向量a＝(x,1)，b＝(1，y)，c＝(2，－4)，且a⊥c，b∥c，则|a＋b|＝(　　)‎ ‎8．（2012·上海卷） 在平行四边形ABCD中，∠A＝，边AB、AD的长分别为2、1.若M、N分别是边BC、CD上的点，且满足＝，则·的取值范围是________．‎ ‎9．（2012·辽宁卷） 已知两个非零向量a，b满足|a＋b|＝|a－b|，则下面结论正确的是(　　)‎ A．a∥b B．a⊥b C．|a|＝|b| D．a＋b＝a－b ‎10．（2012·课标全国卷） 已知向量a，b夹角为45°，且|a|＝1，|‎2a－b|＝，则|b|＝________.‎ ‎＝(　　)‎ A. B．1‎ C. D. ‎13．（2012·北京卷） 已知正方形ABCD的边长为1，点E是AB边上的动点，则·的值为________.·的最大值为________．‎ ‎14．（2012·重庆卷） 设x，y∈R，向量a＝(x,1)，b＝(1，y)，c＝(2，－4)，且a⊥c，b∥c，则|a＋b|＝(　　)‎ A. B. C．2 D．10‎ ‎15．（2012·浙江卷） 在△ABC中，M是BC的中点，AM＝3，BC＝10，则·＝________.‎ ‎16．（2012·湖南卷） 在△ABC中，AB＝2，AC＝3，·＝1，则BC＝(　　)‎ A. B. C．2 D. ‎17．（2012·福建卷） 如图1－4，椭圆E：＋＝1(a＞b＞0)的左焦点为F1，右焦点为F2，离心率e＝，过F1的直线交椭圆于A、B两点，且△ABF2的周长为8.‎ ‎(1)求椭圆E的方程；‎ ‎(2)设动直线l：y＝kx＋m与椭圆E有且只有一个公共点P，且与直线x＝4相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．‎ 图1－4‎ ‎18．（2012·山东卷） 已知向量m＝(sinx,1)，n＝(A>0)，函数f(x)＝m·n的最大值为6.‎ ‎(1)求A；‎ ‎(2)将函数y＝f(x)的图象向左平移个单位，再将所得图象上各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)在上的值域．‎ ‎19．（2012·天津卷） 已知△ABC为等边三角形，AB＝2，设点P，Q满足＝λ，＝(1－λ)，λ∈R.若·＝－，则λ＝(　　)‎ ‎20．（2012·浙江卷） 设a，b是两个非零向量(　　)‎ A．若|a＋b|＝|a|－|b|，则a⊥b B．若a⊥b，则|a＋b|＝|a|－|b|‎ C．若|a＋b|＝|a|－|b|，则存在实数λ，使得b＝λa D．若存在实数λ，使得b＝λa，则|a＋b|＝|a|－|b|‎ ‎21．（2012·四川卷） 设a，b都是非零向量，下列四个条件中，使＝成立的充分条件是(　　)‎ A．a＝－b B．a∥b C．a＝2b D．a∥b且|a|＝|b|‎ ‎22．（2012·山东卷） 如图1－4所示，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P的位置在(0,0)，圆在x轴上沿正向滚动，当圆滚动到圆心位于(2,1)时，的坐标为________．‎ 图1－4‎ ‎ 1. (2011年高考四川卷理科4)如图，正六边形ABCDEF中，=( )‎ ‎(A)0 (B) (C) (D)‎ ‎2. (2011年高考全国卷理科12)设向量满足||=||=1, ,，=，则的最大值等于 ‎ (A)2 (B) (c) (D)1‎ ‎3. (2011年高考浙江卷理科14)若平面向量，满足，，且以向量，为邻边的平行四边形的面积为，则与的夹角的取值范围是 。‎ ‎4.(2011年高考安徽卷理科13)已知向量a，b满足（a+2b）·（a-b）=－6，且，，则a与b的夹角为 .‎ ‎5.(2011年高考重庆卷理科12)已知单位向量的夹角为，则 ‎ ‎6.(2011年高考安徽卷江苏10)已知是夹角为的两个单位向量， 若，则k的值为 .‎ ‎1.（2010全国卷2理数）（8）中，点在上，平方．若，，，，则 ‎（A） （B） （C） （D）‎ ‎2.（2010辽宁理数）(8)平面上O,A,B三点不共线，设，则△OAB的面积等于 ‎(A) (B) ‎ ‎(C) (D) ‎ ‎3.（2010重庆理数）(2) 已知向量a，b满足，则 A. 0 B. C. 4 D. 8‎ ‎4.（2010四川理数）（5）设点M是线段BC的中点，点A在直线BC外，则 ‎（A）8 （B）4 （C） 2 （D）1‎ ‎5.（2010山东理数） (12)定义平面向量之间的一种运算“”如下，对任意的，，令，下面说法错误的是（ ）‎ A.若与共线，则 B. ‎ C.对任意的，有 D. ‎ ‎6.（2010江西理数）13.已知向量，满足，， 与的夹角为60°，则 ‎ ‎7.（2010天津理数）（15）如图，在中，,,‎ ‎,则 .‎ ‎8.（2010广东理数）10.若向量=（1,1,x）, =(1,2,1), =(1,1,1),满足条件=-2,则= .‎ ‎9.（2010江苏卷）15、（本小题满分14分）‎ 在平面直角坐标系xOy中，点A(－1,－2)、B(2,3)、C(－2,－1)。‎ (1) 求以线段AB、AC为邻边的平行四边形两条对角线的长；‎ (2) 设实数t满足()·=0，求t的值。‎ ‎ 1.（2009·广东理6）一质点受到平面上的三个力（单位：牛顿）的作用而处于平衡状态．已知，成角，且，的大小分别为2和4，则的大小为 ‎ A. 6 B. 2 C. D. ‎ ‎2.（2009·浙江理7）设向量，满足：，，．以，，的模为边长构成三角形，则它的边与半径为的圆的公共点个数最多为 ( ) ‎ A． B． C． D．‎ ‎3.（2009·浙江）已知向量，．若向量满足，，则 （ ）‎ A． B． C． D． ‎ ‎4.(2009·山东理7;文.8)设P是△ABC所在平面内的一点，，则（　）‎ A. B. C. D.‎ ‎5.（2009·宁夏海南理9）已知O，N，P在所在平面内，且 ‎，且，则点O，N，P依次是 的 ‎（A）重心 外心 垂心 （B）重心 外心 内心 ‎ ‎（C）外心 重心 垂心 （D）外心 重心 内心 ‎（注：三角形的三条高线交于一点，此点为三角型的垂心）‎ ‎6.（2009·辽宁文理3）平面向量a与b的夹角为，a＝(2,0), | b |＝1，则 | a＋2b |＝‎ ‎（A） （B）2 （C）4 （D）12‎ ‎7.（2009·福建理9，文12）设，，为同一平面内具有相同起点的任意三个非零向量，且满足与不共线， ∣∣=∣∣,则∣ •∣的值一定等于 ‎ ‎8.（2009·江苏）已知向量和向量的夹角为，，则向量和向量的数量积= 。‎ ‎9.（2009·安徽理14）给定两个长度为1的平面向量和，它们的夹角为.，如图所示，点C在以O为圆心的圆弧上变动。若其中,则的最大值是________.‎ ‎10.(天津理.15)在四边形ABCD中，==（1，1），，则四边形ABCD的面积是 ‎ ‎11.(天津15)若等边的边长为，平面内一点M满足,则________.‎ ‎12.（2009·浙江理18）（本题满分14分）在中，角所对的边分别为，且满足， ． ‎ ‎（I）求的面积； （II）若，求的值．‎ ‎13.（2009·广东理16）(本小题满分12分）‎ 已知向量与互相垂直，其中．‎ ‎（1）求和的值；‎