【数学】2018届一轮复习人教A版解三角形的应用教案

【数学】2018届一轮复习人教A版解三角形的应用教案

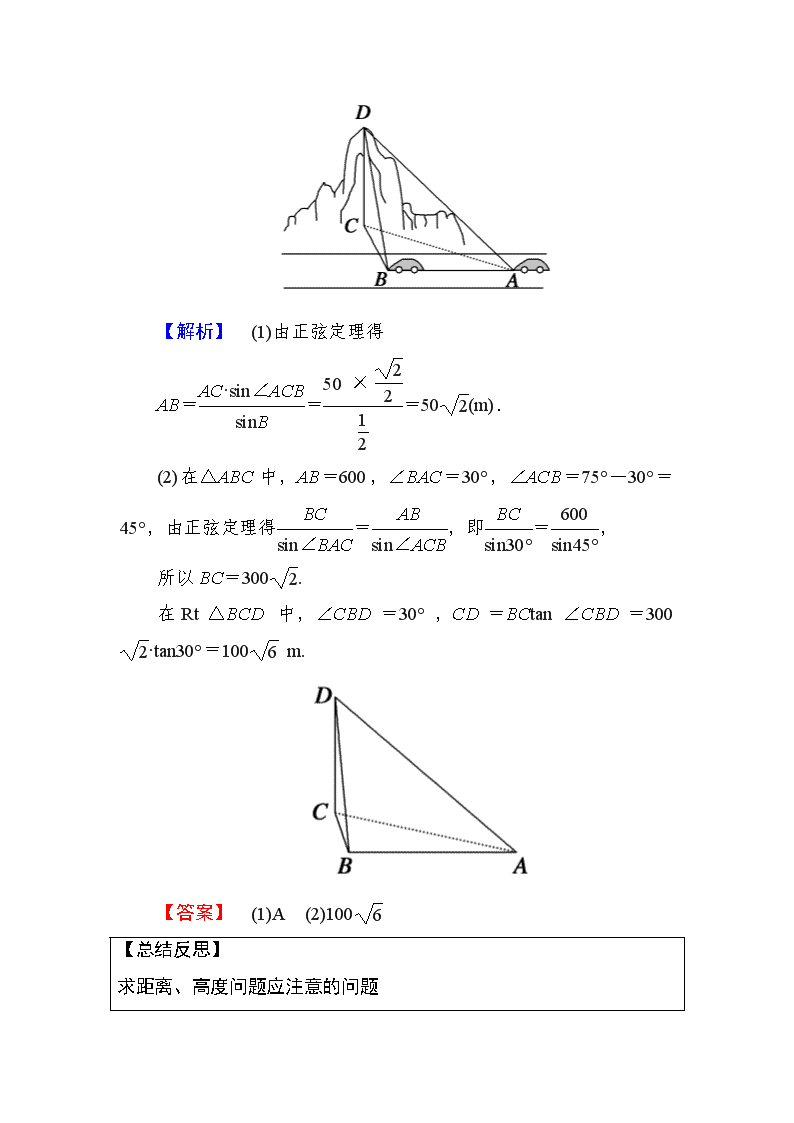
第2课时　解三角形的应用 热点一　　正、余弦定理的实际应用 ‎ ‎【例1】　(1)如图，设A、B两点在河的两岸，一测量者在A的同侧，选定一点C，测出AC的距离为‎50 m，∠ACB＝45°，∠CAB＝105°，则A，B两点的距离为(　　)‎ A．‎50 m　　B．‎50 m　　C．‎25 m　　D. m ‎(2)如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶‎600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD＝________m.‎ ‎【解析】　(1)由正弦定理得 AB＝＝＝50(m)．‎ ‎(2)在△ABC中，AB＝600，∠BAC＝30°，∠ACB＝75°－30°＝45°，由正弦定理得＝，即＝，‎ 所以BC＝300.‎ 在Rt△BCD中，∠CBD＝30°，CD＝BCtan∠CBD＝300·tan30°＝‎100 m.‎ ‎【答案】　(1)A　(2)100 ‎【总结反思】‎ 求距离、高度问题应注意的问题 ‎(1)理解俯角、仰角的概念，它们都是视线与水平线的夹角；理解方向角的概念；‎ ‎(2)选定或确定要创建的三角形，要首先确定所求量所在的三角形，若其他量已知则直接解；若有未知量，则把未知量放在另一确定三角形中求解．‎ ‎(3)确定用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理.‎ ‎(2017·台州模拟)在O点测量到远处有一物体在做匀速直线运动，开始时该物体位于P点，一分钟后其位置在Q点，且∠POQ＝90°，再过两分钟后，该物体位于R点，且∠QOR＝60°，则tan2∠OPQ的值等于(　　)‎ A. B. C. D．以上均不正确 解析：设PQ＝x，QR＝2x，∠OPQ＝α.如图，‎ 因为∠POQ＝90°，∠QOR＝60°，‎ 所以∠ORP＝30°－α，‎ 在Rt△OPQ中，OQ＝xsinα.①‎ 在△OQR中，由正弦定理，‎ 得＝，‎ 解得OQ＝sin(30°－α)．②‎ 由①②，得xsinα＝sin(30°－α)，‎ 解得tanα＝，即tan2α＝.‎ 答案：A 热点二　三角形与平面几何的综合问题 ‎ ‎【例2】　(2017·广东惠州调研)如图所示，在四边形ABCD中，∠D＝2∠B，且AD＝1，CD＝3，cosB＝.‎ ‎(1)求△ACD的面积；‎ ‎(2)若BC＝2，求AB的长．‎ ‎【解】　(1)cosD＝cos2B＝2cos2B－1＝－.‎ 因为∠D∈(0，π)，所以sinD＝，‎ 所以△ACD的面积 S＝·AD·CD·sinD＝.‎ ‎(2)在△ACD中，AC2＝AD2＋DC2－2AD·DC·cosD＝12，所以AC＝2.在△ABC中，AC2＝AB2＋BC2－2AB·BC·cosB＝12，把已知条件代入并化简得AB2－4AB＝0，因为AB≠0，所以AB＝4.‎ ‎【总结反思】‎ 此类题目求解时，一般有如下思路：‎ ‎(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；‎ ‎(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果．‎ 做题过程中，要用到平面几何中的一些知识点，如相似三角形的边角关系、平行四边形的一些性质，要把这些性质与正弦、余弦定理有机结合，顺利解决问题.‎ ‎(2017·福建师大附中联考)如图，在矩形ABCD中，AB＝，BC＝3，E在AC上，若BE⊥AC，则ED＝________.‎ 解析：在Rt△ABC中，BC＝3，AB＝，所以∠BAC＝60°.‎ 因为BE⊥AC，AB＝，所以AE＝，‎ 在△EAD中，∠EAD＝30°，AD＝3，‎ 由余弦定理知，ED2＝AE2＋AD2－2AE·AD·cos∠EAD＝＋9－2××3×＝，故ED＝.‎ 答案： 热点三 三角形中的最值问题 ‎ ‎【例3】　(2017·临川一中模拟)已知f(x)＝cos2x＋2sinsin(π－x)，x∈R.‎ ‎(1)求f(x)的最小正周期及单调增区间；‎ ‎(2)已知锐角△ABC的内角A，B，C的对边分别为a，b，c，且f(A ‎)＝－，a＝3，求BC边上的高的最大值．‎ ‎【解】　(1)f(x)＝cos2x－sin2x＝－2sin，‎ ‎∴f(x)的最小正周期为π，‎ 令2kπ＋≤2x－≤2kπ＋π(k∈Z)，得kπ＋π≤x≤kπ＋π(k∈Z)，‎ ‎∴单调递增区间为(k∈Z)．‎ ‎(2)由f(A)＝－得sin＝，又A∈，∴A＝.由余弦定理得a2＝b2＋c2－2bccosA，得9＝b2＋c2－bc≥bc，即bc≤9(当且仅当b＝c时取等号)．‎ 设BC边上的高为h，由三角形等面积法知ah＝bcsinA，得3h＝bc≤，∴h≤，即h的最大值为.‎ ‎【总结反思】‎ 解三角形的最值问题常需结合基本不等式求解，关键是由余弦定理得到两边关系，再结合不等式求解最值问题，或者将所求转化为某个角的三角函数，借助三角函数的值域求范围.‎ 在△ABC中，a2＋c2＝b2＋ac.‎ ‎(1)求∠B的大小；‎ ‎(2)求cosA＋cosC的最大值．‎ 解：(1)由余弦定理及题设得 cosB＝＝＝.‎ 又0<∠B<π，所以∠B＝.‎ ‎(2)由(1)知∠A＋∠C＝，则cosA＋cosC＝cosA＋cos＝cosA－cosA＋sinA ‎＝cosA＋sinA＝cos(A－)．‎ 因为0<∠A<，所以当∠A＝时，cosA＋cosC取得最大值1.‎ 热点四　　三角形与不等式的综合应用 ‎ ‎【例4】　已知△ABC的内角A，B，C满足sin‎2A＋sin(A－B＋C)＝sin(C－A－B)＋，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，则下列不等式一定成立的是(　　)‎ A．bc(b＋c)>8 B．ab(a＋b)>16 C．6≤abc≤12 D．12≤abc≤24‎ ‎【解析】　因为A＋B＋C＝π，由sin‎2A＋sin(A－B＋C)＝sin(C－A－B)＋ 得sin‎2A＋sin2B＋sin‎2C＝，‎ 即sin[(A＋B)＋(A－B)]＋sin[(A＋B)－(A－B)]＋sin‎2C＝，‎ 整理得2sinCcos(A－B)＋2sinCcosC＝2sinC[cos(A－B)－cos(A＋B)]＝，‎ 整理得4sinA·sinBsinC＝，即sinAsinBsinC＝.‎ 又S＝absinC＝bcsinA＝ca·sinB，‎ 因此S3＝a2b‎2c2sinAsinBsinC＝a2b‎2c2.‎ 由1≤S≤2得1≤a2b‎2c2≤23，‎ 即8≤abc≤16，因此选项C、D不一定成立．‎ 又b＋c>a>0，因此bc·(b＋c)>bc·a≥8，即bc(b＋c)>8，选项A一定成立．‎ 又a＋b>c>0，因此ab(a＋b)>ab·c≥8，即ab(a＋b)>8，显然不能得出ab(a＋b)>16，选项B不一定成立．‎ 综上所述，选A.‎ ‎【答案】　A ‎【总结反思】‎ 三角形与不等式的综合常结合不等式的性质与基本不等式.‎ 在△ABC中，角A，B，C的对应边分别为a，b，c，满足＋≥1，则角A的范围是(　　)‎ A. B. C. D. 解析：由＋≥1，‎ 得b(a＋b)＋c(a＋c)≥(a＋c)(a＋b)，‎ 化简得b2＋c2－a2≥bc，即≥，‎ 即cosA≥(0

查看更多