高考数学一轮复习精品学案：第4讲 基本初等函数

高考数学一轮复习精品学案：第4讲 基本初等函数

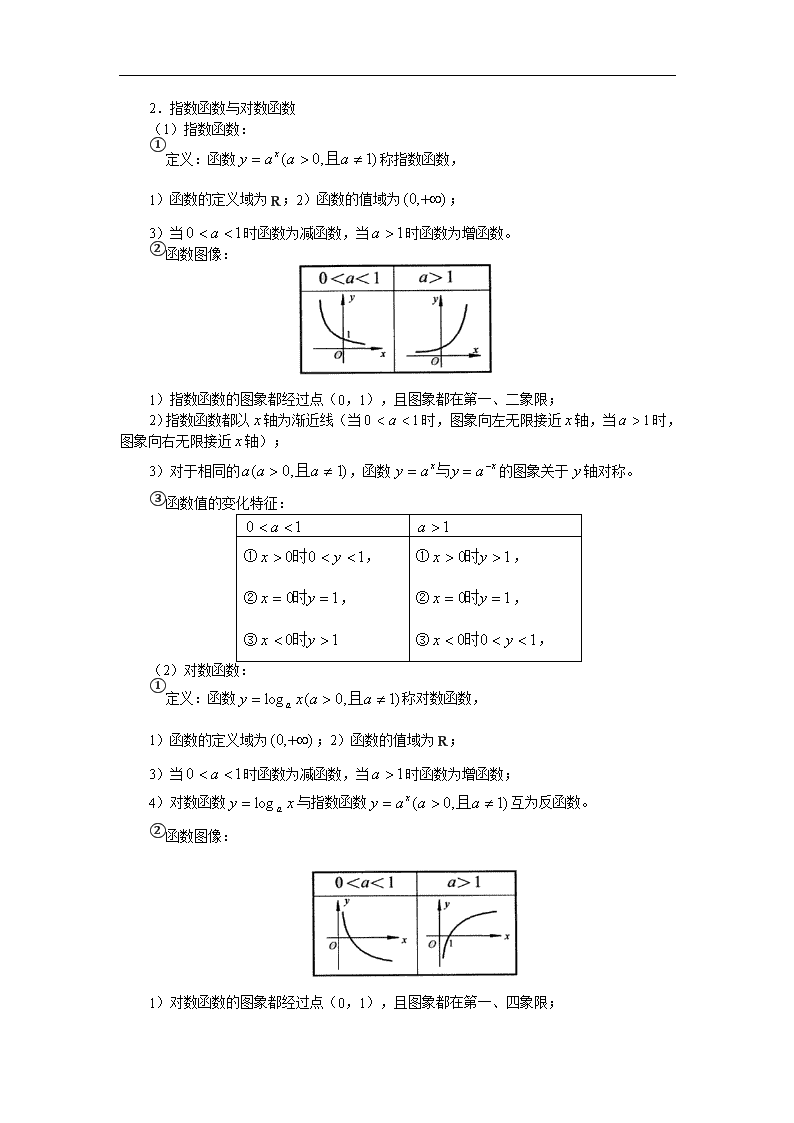
‎2013年普通高考数学科一轮复习精品学案 第4讲 基本初等函数 一．课标要求 ‎1．指数函数 ‎（1）通过具体实例（如细胞的分裂，考古中所用的14C的衰减，药物在人体内残留量的变化等），了解指数函数模型的实际背景；‎ ‎（2）理解有理指数幂的含义，通过具体实例了解实数指数幂的意义，掌握幂的运算。‎ ‎（3）理解指数函数的概念和意义，能借助计算器或计算机画出具体指数函数的图象，探索并理解指数函数的单调性与特殊点；‎ ‎（4）在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型。‎ ‎2．对数函数 ‎（1）理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；通过阅读材料，了解对数的发现历史以及对简化运算的作用；‎ ‎（2）通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点；‎ ‎3．知道指数函数与对数函数互为反函数（a＞0，a≠1）。‎ 二．命题走向 指数函数、对数函数、幂函数是三类常见的重要函数，在历年的高考题中都占据着重要的地位。从近几年的高考形势来看，对指数函数、对数函数、幂函数的考查，大多以基本函数的性质为依托，结合运算推理，能运用它们的性质解决具体问题。为此，我们要熟练掌握指数、对数运算法则，明确算理，能对常见的指数型函数、对数型函数进行变形处理。‎ 预测2013年对本节的考察是：‎ ‎1．题型有两个选择题和一个解答题；‎ ‎2．题目形式多以指数函数、对数函数、幂函数为载体的复合函数来考察函数的性质。同时它们与其它知识点交汇命题，则难度会加大。‎ 三．要点精讲 ‎1．指数与对数运算 ‎（1）根式的概念：‎ ‎①定义：若一个数的次方等于，则这个数称的次方根。即若，则称的次方根，‎ ‎1）当为奇数时，次方根记作；‎ ‎2）当为偶数时，负数没有次方根，而正数有两个次方根且互为相反数，记作。‎ ‎②性质：1）；2）当为奇数时，；‎ ‎3）当为偶数时，。‎ ‎（2）．幂的有关概念 ‎①规定：1）N*；2）；‎ ‎ n个 ‎3）Q，4）、N* 且。‎ ‎②性质：1）、Q）；‎ ‎2）、 Q）；‎ ‎3） Q）。‎ ‎（注）上述性质对r、R均适用。‎ ‎（3）．对数的概念 ‎①定义：如果的b次幂等于N，就是，那么数称以为底N的对数，记作其中称对数的底，N称真数。‎ ‎1）以10为底的对数称常用对数，记作；‎ ‎2）以无理数为底的对数称自然对数，，记作；‎ ‎②基本性质：‎ ‎1）真数N为正数（负数和零无对数）；2）；‎ ‎3）；4）对数恒等式：。‎ ‎③运算性质：如果则 ‎1）；‎ ‎2）；‎ ‎3）R）。‎ ‎④换底公式：‎ ‎1）；2）。‎ ‎2．指数函数与对数函数 ‎（1）指数函数：‎ ‎①定义：函数称指数函数，‎ ‎1）函数的定义域为R；2）函数的值域为；‎ ‎3）当时函数为减函数，当时函数为增函数。‎ ‎②函数图像：‎ ‎1）指数函数的图象都经过点（0，1），且图象都在第一、二象限；‎ ‎2）指数函数都以轴为渐近线（当时，图象向左无限接近轴，当时，图象向右无限接近轴）；‎ ‎3）对于相同的，函数的图象关于轴对称。‎ ‎①，‎ ‎②，‎ ‎③‎ ‎①，‎ ‎②，‎ ‎③，‎ ‎③函数值的变化特征：‎ ‎（2）对数函数：‎ ‎①定义：函数称对数函数，‎ ‎1）函数的定义域为；2）函数的值域为R；‎ ‎3）当时函数为减函数，当时函数为增函数；‎ ‎4）对数函数与指数函数互为反函数。‎ ‎②函数图像：‎ ‎1）对数函数的图象都经过点（0，1），且图象都在第一、四象限；‎ ‎2）对数函数都以轴为渐近线（当时，图象向上无限接近轴；当时，图象向下无限接近轴）；‎ ‎4）对于相同的，函数的图象关于轴对称。‎ ‎③函数值的变化特征：‎ ‎①，‎ ‎②，‎ ‎③.‎ ‎①，‎ ‎②，‎ ‎③.‎ ‎ ‎ 四．典例解析 题型1：指数运算 例1．（1）计算：；‎ ‎（2）化简：。‎ 解：（1）原式=‎ ‎；‎ ‎（2）原式=‎ ‎。‎ 点评：根式的化简求值问题就是将根式化成分数指数幂的形式，然后利用分数指数幂的运算性质求解，对化简求值的结果，一般用分数指数幂的形式保留；一般的进行指数幂运算时，化负指数为正指数，化根式为分数指数幂，化小数为分数运算，同时兼顾运算的顺序。‎ 例2．已知，求的值。‎ 解：∵，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ 又∵，‎ ‎∴。‎ 点评：本题直接代入条件求解繁琐，故应先化简变形，创造条件简化运算。‎ 题型2：对数运算 例3．计算 ‎（1）；（2）；‎ ‎（3）。‎ 解：（1）原式 ‎ ；‎ ‎（2）原式 ‎ ；‎ ‎（3）分子=；‎ 分母=；‎ 原式=。‎ 点评：这是一组很基本的对数运算的练习题，虽然在考试中这些运算要求并不高，但是数式运算是学习数学的基本功，通过这样的运算练习熟练掌握运算公式、法则，以及学习数式变换的各种技巧。‎ 例4．设、、为正数，且满足 ‎ ‎（1）求证：；‎ ‎（2）若，，求、、的值。‎ 证明：（1）左边 ‎；‎ 解：（2）由得，‎ ‎∴……………①‎ 由得………… ……………②‎ 由①②得……………………………………③‎ 由①得，代入得，‎ ‎∵， ∴………………………………④‎ 由③、④解得，，从而。‎ 点评：对于含对数因式的证明和求值问题，还是以对数运算法则为主，将代数式化简到最见形式再来处理即可。‎ 题型3：指数、对数方程 例5．设关于的方程R），‎ ‎（1）若方程有实数解，求实数b的取值范围；‎ ‎（2）当方程有实数解时，讨论方程实根的个数，并求出方程的解。‎ 解：（1）原方程为，‎ ‎，‎ 时方程有实数解；‎ ‎（2）①当时，，∴方程有唯一解；‎ ‎②当时，.‎ 的解为；‎ 令 的解为；‎ 综合①、②，得 ‎1）当时原方程有两解：；‎ ‎2）当时，原方程有唯一解；‎ ‎3）当时，原方程无解。‎ 点评：具有一些综合性的指数、对数问题，问题的解答涉及指数、对数函数，二次函数、参数讨论、方程讨论等各种基本能力，这也是指数、对数问题的特点，题型非常广泛，应通过解题学习不断积累经验。‎ 例6．（2006辽宁 文13）方程的解为 。‎ 解：考察对数运算。原方程变形为，即，得。且有。从而结果为。‎ 点评：上面两例是关于含指数式、对数式等式的形式，解题思路是转化为不含指数、对数因式的普通等式或方程的形式，再来求解。‎ 题型4：指数函数的概念与性质 例7．设（ ）‎ A．0 　B．‎1 C．2 D．3‎ 解：C；，。‎ 点评：利用指数函数、对数函数的概念，求解函数的值。‎ 例8．已知试求函数f(x)的单调区间。‎ 解：令，则x=，t∈R。‎ 所以即，（x∈R）。‎ 因为f(－x)=f(x)，所以f(x)为偶函数，故只需讨论f(x)在[0，+∞）上的单调性。‎ 任取，，且使，则 ‎（1）当a>1时，由，有，，所以 ‎，即f(x)在[0，+∞]上单调递增。‎ ‎（2）当01时，函数y=logax和y=(1－a)x的图象只可能是( )‎ 解：当a>1时，函数y=logax的图象只能在A和C中选，‎ 又a>1时，y=(1－a)x为减函数。‎ 答案：B 点评：要正确识别函数图像，一是熟悉各种基本函数的图像，二是把握图像的性质，根据图像的性质去判断，如过定点、定义域、值域、单调性、奇偶性。‎ 例14．设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D。‎ ‎（1）求点D的坐标；‎ ‎（2）当△ABC的面积大于1时, 求实数a的取值范围。‎ 解：（1）易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4))，‎ 所以由中点公式得D(a+2, log2 )。‎ ‎（2）S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2, ‎ 其中A′,B′,C′为A,B,C在x轴上的射影。‎ 由S△ABC= log2>1, 得0< a<2－2。‎ 点评：解题过程中用到了对数函数性质，注意底数分类来处理，根据函数的性质来处理复杂问题。‎ 题型8：指数函数、对数函数综合问题 例15．在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…，对每个自然数n点Pn位于函数y=2000()x(0bn+1>bn+2。‎ 则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn，‎ 即()2+()－1>0，‎ 解得a<－5(1+)或a>5(－1)。 ‎ ‎∴5(－1)

查看更多