2019-2020学年安徽省蚌埠市第二中学高二上学期期中考试数学（文）试题 word版

2019-2020学年安徽省蚌埠市第二中学高二上学期期中考试数学（文）试题 word版

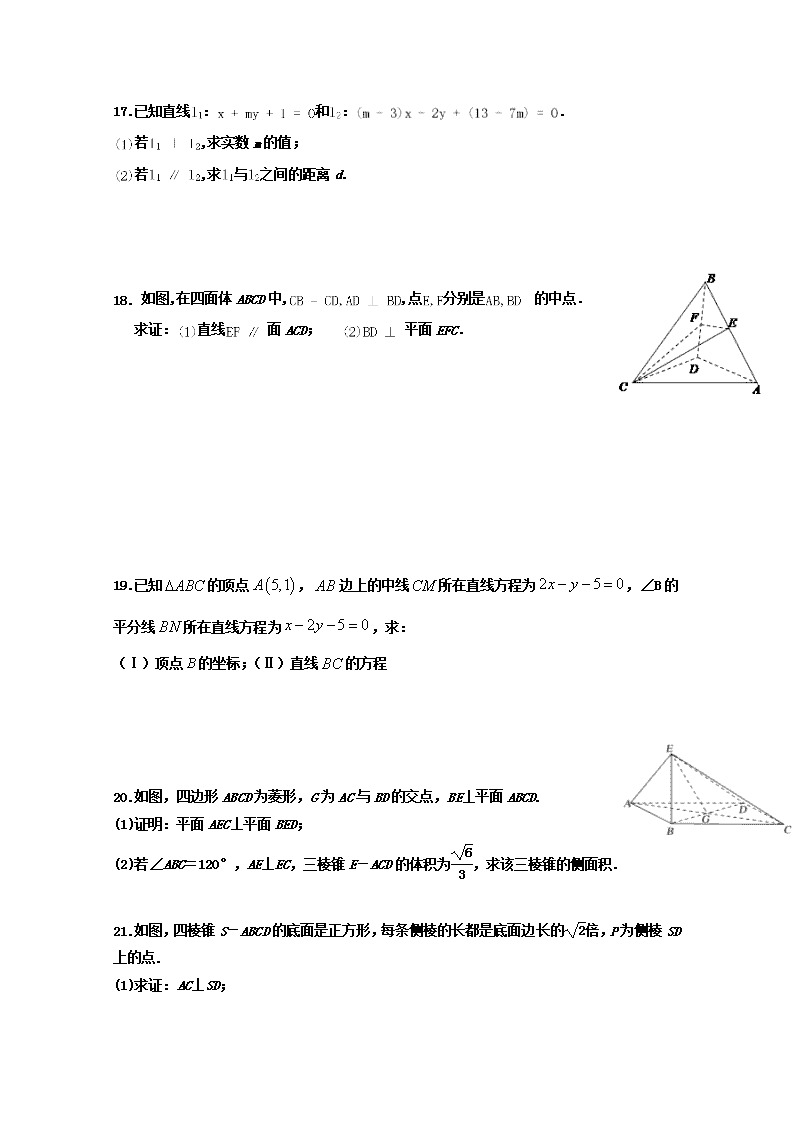
蚌埠二中2019-2020学年第一学期期中考试 高二数学试题（文科）‎ 第I卷（选择题）‎ 一 选择题（每小题5分，共计60分）‎ ‎1.以下命题中正确的是(    )‎ A. 以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 B. 以直角梯形的一腰为轴旋转所得的旋转体是圆台 C. 有一个面是多边形,其余各面都是三角形的几何体叫做棱锥 D. 圆锥的侧面展开图为扇形,这个扇形的半径为圆锥底面圆的半径 ‎2.已知空间三条直线l、m、若l与m异面,且l与n异面,则(    )‎ A. m与n异面 B. m与n相交 C. m与n平行 D. m与n异面、相交、平行均有可能 ‎3.直线的倾斜角为(    )‎ A. B. C. D. ‎ ‎4.已知m，n为两条不同的直线，，为两个不同的平面，则下列命题中正确的有(    ) ，，， ， ，， ，‎ A. 0个 B. 1个 C. 2个 D. 3个 ‎5.在四面体中,点E、F、G、H分别在直线AD、AB、CD、BC上，若直线EF和GH相交,则它们的交点一定(    ) ‎ A. 在直线DB上 B. 在直线AB上 C. 在直线CB上 D. 都不对 ‎6.方程表示以为圆心,4为半径的圆,则D,E,F的值分别为(    )‎ A. 4,,3 B. ,6,‎3 ‎C. ,,3 D. 4,,‎ ‎7.已知水平放置的是按“斜二测画法”得到如图所示的直观图,其中,,那么原中的大小是(    )‎ A. B. C. D. ‎ ‎8.若为圆的弦的中点，则直线的方程是 ‎ A. B. C. D.‎ ‎9.在三棱锥中,平面ABC,,,,则三棱锥的外接球的表面积是(    )‎ A. B. C. D. ‎ ‎10.圆上存在两点关于直线对称,则 的最小值为(    )‎ A. 8 B. ‎9 ‎C. 16 D. 18‎ ‎11.在棱长为2的正方体中，P是内不含边界的一个动点，若 ‎，则线段长的取值范围为(    )‎ A. B. C. D. ‎ ‎12.直线与曲线有两个不同交点,则实数的k的取值范围是(    )‎ A. B. C. D. ‎ ‎ 第II卷（非选择题）‎ 二 填空题（每小题5分，共计20分）‎ ‎13.平面两两相交,为三条交线,且,则b与c的位置关系是_________． 14.求经过点，且在轴上的截距是在轴上的截距2倍的直线方程为________ .‎ ‎15.如图,二面角的大小是,线段,AB与l所成的角为则AB与平面所成的角的正弦值是______．‎ ‎16.已知圆的方程为,是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是______ ．‎ 三 解答题（第17题10分，18题到22题每题12分，共计70分）‎ ‎17.已知直线：和：． 若,求实数m的值； 若,求与之间的距离d．‎ 18. 如图,在四面体ABCD中,,点分别是 的中点．   求证：直线面ACD；  平面EFC．‎ ‎19.已知的顶点，边上的中线所在直线方程为，∠B的平分线所在直线方程为，求：‎ ‎（Ⅰ）顶点的坐标；（Ⅱ）直线的方程 ‎ 20.如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.‎ ‎(1)证明：平面AEC⊥平面BED；‎ ‎(2)若∠ABC＝120°，AE⊥EC，三棱锥E－ACD的体积为，求该三棱锥的侧面积.‎ ‎21.如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是底面边长的倍，P为侧棱SD上的点.‎ ‎(1)求证：AC⊥SD；‎ ‎(2)若SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC？若存在，求SE∶EC；若不存在，试说明理由.‎ ‎22.已知圆C的圆心在直线上,且与直线相切于点．Ⅰ求圆C方程；Ⅱ是否存在过点的直线l与圆C交于E、F两点,且的面积是为坐标原点若存在,求出直线l的方程,若不存在,请说明理由．‎ 蚌埠二中2019---2020学年度高二第一学期期中数学试题（文）‎ 一 A D D B A D C A C B C A 二13. 14. 15. 16.‎ 三17. 解：直线：和：, 当时,,解得； 由可得,解得或, 当时,与重合,应舍去, 当时,可得：,：,即, 由平行线间的距离公式可得 ‎18.证明：,F分别是AB,BD的中点．‎ 是的中位线,, 面ACD,面ACD,直线面ACD； ,,, ,F是的中点,, 又, 平面CEF,平面CEF, 得平面 面EFC． 19.（Ⅰ）设，则中点坐标为：‎ ‎，即：‎ 又，解得：，‎ ‎（Ⅱ）设点关于的对称点为 则，解得：‎ 边所在的直线方程为：，即：‎ ‎20(1)证明　因为四边形ABCD为菱形，所以AC⊥BD.‎ 因为BE⊥平面ABCD，AC⊂平面ABCD，所以AC⊥BE.‎ 又BD∩BE＝B，故AC⊥平面BED.‎ 又AC⊂平面AEC，所以平面AEC⊥平面BED.‎ ‎(2)解　设AB＝x，在菱形ABCD中，由∠ABC＝120°，‎ 可得AG＝GC＝x，GB＝GD＝.‎ 因为AE⊥EC，所以在Rt△AEC中，可得EG＝x.‎ 由BE⊥平面ABCD，BG⊂平面ABCD，‎ 得BE⊥BG，知△EBG为直角三角形，可得BE＝x.‎ 由已知得，三棱锥E－ACD的体积V三棱锥E－ACD＝×·AC·GD·BE＝x3＝，故x＝2.‎ 从而可得AE＝EC＝ED＝. 所以△EAC的面积为3，△EAD的面积与△ECD的面积均为.故三棱锥E－ACD的侧面积为3＋2.‎ ‎21.(1)证明　连接BD，设AC交BD于点O，连接SO，‎ 由题意得四棱锥S－ABCD是正四棱锥，所以SO⊥AC.在正方形ABCD中，AC⊥BD，又SO∩BD＝O，所以AC⊥平面SBD，因为SD⊂平面SBD，所以AC⊥SD.‎ ‎(2)解　在棱SC上存在一点E，使得BE∥平面PAC.‎ 连接OP.设正方形ABCD的边长为a，则SC＝SD＝a.‎ 由SD⊥平面PAC得SD⊥PC，易求得PD＝.‎ 故可在SP上取一点N，使得PN＝PD.‎ 过点N作PC的平行线与SC交于点E，连接BE，BN.‎ 在△BDN中，易得BN∥PO，又因为NE∥PC，NE⊂平面BNE，BN⊂平面BNE，BN∩NE＝N，PO⊂平面PAC，PC⊂平面PAC，PO∩PC＝P，‎ 所以平面BEN∥平面PAC，所以BE∥平面PAC.‎ 因为SN∶NP＝2∶1，所以SE∶EC＝2∶1. 22.Ⅰ过切点且与垂直的直线为,即． 与直线联立,解得,, 圆心为,半径, 所求圆的方程为． Ⅱ当斜率不存在时,此时直线l方程为,原点到直线的距离为, 同时令代入圆方程得,, 满足题意,此时方程为． 当斜率存在时,设直线l的方程为, 圆心到直线l的距离, 设EF的中点为D,连接CD,则必有, 在中,, ,原点到直线l的距离, , 整理,得,不存在这样的实数k． 综上所述,所求的直线方程为．‎