2020届河南八市重点高中联盟领军考试数学高三（文数）数学答案

2020届河南八市重点高中联盟领军考试数学高三（文数）数学答案

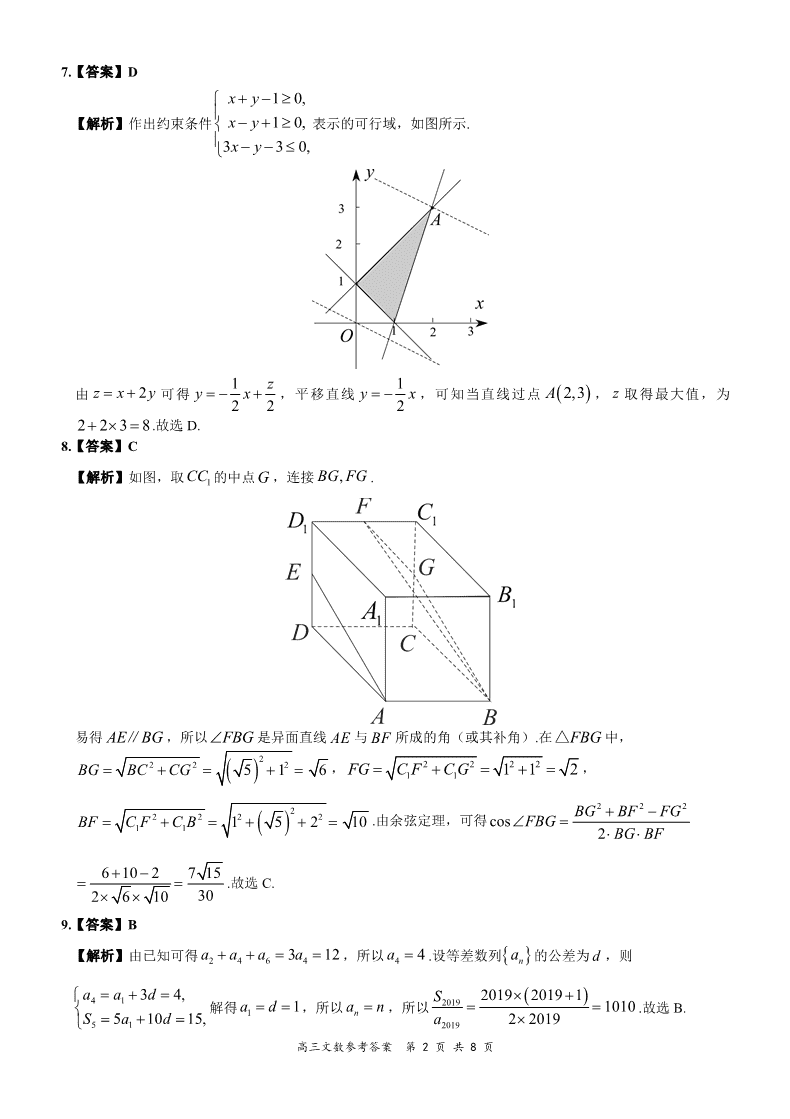
高三文数参考答案 第 1 页 共 8 页 2019—2020 学年度上期八市重点高中联盟 “领军考试”高三数学参考答（文数） 1.【答案】C 【解析】由已知得  1 xxBUC ，又  | 2A x x  ，所以    2＞xxBA U C .故选 C. 2.【答案】B 【解析】由已知可得，     10000lg3 πcos22019100003 π79813 π2019           ffff 12 4 52     .故选 B. 3.【答案】C 【解析】由已知可得 1 lnexy xx       ，所以在点（1,1）处的切线的斜率 e)01(e1 k ，所以切线方程 为  1 e 1y x   ，即 e e 1 0x y    .故选 C. 4.【答案】D 【解析】对于 A，当 1 1a b    时， 1 1 a b  ，故错误； 对于 B，当 11 2a b   时， 1 12a b   ，所以  ln 0a b  ，故错误； 对于 C，当 1 2a b    时， 2 2a b ，故错误； 对于 D， 因为 a b ，所以 3 3a b ，故正确. 故选 D. 5.【答案】B 【解析】由已知可得  1 1 1 1 1 2 2 2 2 2AE AC CE AC CB AC AD AC AC CD AC CD                      .所 以 1 2   ， 1 2    ，所以 0   .故选 B. 6.【答案】B 【解析】由已知可得函数的定义域为 0xx ，     3 3 e e e ex x x x x xf x f x       ，所以函数  f x 是 偶函数，图象关于 y 轴对称，可排除选项 A，C；又当 0x  时， 3 0x  ， 2e 1e e 0e x x x x     ，所以   0f x  ， 可排除选项 D.故选 B. 高三文数参考答案 第 2 页 共 8 页 7.【答案】D 【解析】作出约束条件 1 0, 1 0, 3 3 0, x y x y x y            表示的可行域，如图所示. 由 2z x y  可得 1 2 2 zy x   ，平移直线 1 2y x  ，可知当直线过点  2,3A ， z 取得最大值，为 2 2 3 8   .故选 D. 8.【答案】C 【解析】如图，取 1CC 的中点G ，连接 ,BG FG . 易得 AE BG∥ ，所以 FBG 是异面直线 AE 与 BF 所成的角（或其补角）.在 FBG△ 中，  22 2 25 1 6BG BC CG     ， 2 2 2 2 1 1 1 1 2FG C F C G     ，  22 2 2 2 1 1 1 5 2 10BF C F C B      .由余弦定理，可得 2 2 2 cos 2 BG BF FGFBG BG BF      6 10 2 7 15 302 6 10      .故选 C. 9.【答案】B 【解析】由已知可得 2 4 6 43 12a a a a    ，所以 4 4a  .设等差数列 na 的公差为 d ，则      ,15105 ,43 15 14 daS daa 解得 1 1a d  ，所以 na n ，所以  2019 2019 2019 2019 1 10102 2019 S a    .故选 B. 高三文数参考答案 第 3 页 共 8 页 10.【答案】B 【解析】由图象得， 2A  ， 3 π2 4 π 12 π54      T ，则 3π2  T  .又 212 π5     f ，所以 )(π22 π3 12 π53 Z kk ，所以 )(π24 π Z kk .又因为 2 π＜ ，所以 4 π ，所以       4 π3sin2)( xxf .对于 A，当 4 πx 时， 24 π     f ，为函数最小值，故 A 正确；对于 B，当 12 πx 时， 24 π 12 π3sin212 π          f ，所以函数图象关于直线 12 πx 对称，不关于点      012 π ， 对称，故 B 错误；对于 C，由 π22 π 4 π3π22 π kxk  ，可得 )π(3 2 12 ππ3 2 4 π Z kkxk ，令 0k  ，可 得 12 π 4 π  x ，所以  f x 在区间     0,4 π 上单调递增，故 C 正确； 对于 D，由       4 π3sin2 xy 的图象向左平移 6 π 个单位得到                4 π3sin24 π 6 π3sin2 xxy ，故 D 正确.故选 B. 11.【答案】D 【解析】如图，连接 ,AC BD 交于点 E ，取 PC 的中点O ， 连接 OE . 可得OE PA∥ .又因为 PA  底面 ABCD ，所以OE  底面 ABCD ，所以 OP OC OA OB OD    ，所以点O 为四棱锥 P ABCD 的外接球的 球心，其半径为  221 1 31 2 22 2 2OC PC    ，所以外接球的体积 2 π9 2 3 3 π4π3 4 3 3      RV .故选 D. 12.【答案】A 【解析】由正弦定理，可得3sin cos sin cos 0C A A C  ，即  sin 2sin cos 0A C C A   ，即 sin 2sin cos 0B C A  ，进一步由正弦定理，可得 2 cos 0b c A  ，以由余弦定理，可得 2 2 2 2 02 b c ab c bc     ，即 2 2 22b a c  ，所以 2 2 2 2 2 2 2 2 232cos 2 2 4 a ca ca c b a cB ac ac ac       2 3 3 4 2 ac ac   ，当且仅当 2 4 3 3c  ， 2 4 3 3b  ， 2 4 3a  时取等号，又因为 π0 ＜＜B ，所以     6 π,0B ， 所以 B 的最大值为 6 π .故选 A. 高三文数参考答案 第 4 页 共 8 页 13.【答案】 5 【解析】由已知可得  2,2 x  a b ，又  a b a，所以   2 3 2 2 0x      a b a ，解得 5x   . 14.【答案】3399 【解析】设比萨斜塔的高度为 h 米，则由已知可得 4.09 4.09 58.4sin3.99 0.07h    米.设圆形地基的半径为 r 米， 则 285π 2 r ，解得 95 9.7r   ，所以比萨斜塔的侧面积为 33994.587.932π2  rhS 平方米. 15.【答案】 2 【解析】由 2 1n na a   可得 2 1 n n a a   ，则 2 4 1 n n a a   ，所以 4n na a  ，所以数列 na 是以 4 为周期的周期 数列，所以 2019 2020 504 4 3 504 4 4 3 4 1 2 1 2a a a a a a a a         . 16.【答案】 4,0 【解析】函数   3 26 9f x x x x a    有三个不同的零点，则函数  f x 有两个极值点，且极小值小于 0， 极大值大于 0.由   23 12 9 0f x x x     ，解得 1 21, 3x x  ，所以当 1x  时，   0f x  ，  f x 单调 递增；当1 3x  时，   0f x  ，  f x 单调递减；当 3x  时，   0f x  ，  f x 单调递增，所以  f x 的极小值为  3f a ＜0，极大值为  1 4f a  ＞0，所以解得 4 0a   . 17.【解析】（1）因为 3 2 6 a b ， 所以 2 2 23 2 9 12 4 36    a b a a b b ，……………………2 分 所以36 12 2 3cos 36 36     ， 解得 1cos 2   .…………………………4 分 又因为  π,0 ，所以 3 π .…………………………5 分 （2）由（1）可得 1cos 2 3 32     a b a b .…………………………6 分 所以    2 22 2 2 3 2     a b a b a a b b 2 22 2 3 3 2 3      1  .…………………………10 分 高三文数参考答案 第 5 页 共 8 页 18.【解析】（1）因为 2 3 4,2 ,3 a aa 成等差数列，所以   2 432 2 3a a a   ， 即 2 3 1 1 14 3a q a q a q  ，整理得 2 3 04qq   . 解得 3q  或 1q  （舍去）.………………………………4 分 又因为 1 3a  ， 所以 1 1 1 33 3 nn n na a q     .…………………………6 分 （2）由（1）可得 3n n n n nb a   .…………………………7 分 所以 2 1 2 3 3 3n n nT     ，① 132 33 1 3 2 3 1 3 1  nnn nnT  ，②……………………9 分 由①  ②得 2 1 2 3 3 3 1 1 1 3 3n n n nT      11 32 23 2 1 3 3 11 3 113 1          nn n nn .…………………………11 分 所以 nn nT 34 23 4 3   .………………………………12 分 19.【解析】（1）因为 3 cos cos a b c A C  ，所以  cos 3 cos 0a C c b A   ， 由正弦定理，可得  sin cos sin 3sin cos 0A C C B A   ， 即sin cos sin cos 3sin cosA C C A B A  ， 即  sin 3sin cosA C B A  ， 即sin 3sin cosB B A .…………………………3 分 又因为 π0 ＜＜B ，所以sin 0B  ， 所以 1cos 3A  . 又因为 π0 ＜＜A ，所以 2 2 2sin 1 cos 3A A   ，…………………………5 分 所以 1 2 2 4 2sin 2 2sin cos 2 3 3 9A A A     .…………………………6 分 高三文数参考答案 第 6 页 共 8 页 （2）因为 1 1 2 2sin 22 2 3ABC bc A bcS   △ ， 所以 3bc  .………………………………8 分 又由余弦定理，可得 2 2 2 cos 2 b c aA bc   ， 即 2 21 1 3 2 3 b c   ，所以 2 2 3b c  ， 所以 2 2 2 3 2 3b c bc     ， 即 2 9b c  ，解得 3b c  （ 3 已舍去）.…………………………12 分 20.【解析】（1）由题意知，总生产成本为   211000000 50 100G x x x   ， 所以     1000000 50100 G x xf x x x     .……………………2 分 又   1000000 100000050 2 50 250100 100 x xf x x x        ， 当且仅当 1000000 100 x x  ，即 10000x  时，  f x 取得最小值 250 元. 即该公司生产 1 万只垃圾桶时，使得每只平均所需成本费用最少，且每只的成本费用为 250 元.………6 分 （2）由已知可得，利润     211000000 50 100g x ax G x xx m n x x                 21 1 50 1000000100 x m xn         .…………………………8 分 因为当产量为 15000 只时利润最大，此时每只售价为 300 元， 所以 1 1 0,100 15000 300, 50 15000,1 12 100 n m n m n                      解得 250m  ， 300n  .…………………………12 分 高三文数参考答案 第 7 页 共 8 页 21.【解析】（1）因为 ABC△ 为等边三角形， D 是 AC 边的中点， 所以 AC BD . 又 1A A  平面 ABC ， BD  平面 ABC ， 所以 1AA BD .………………………………3 分 又 1AC AA A ，所以 BD  平面 11ACC A . 又 BD  平面 1BDC ，所以平面 1BDC  平面 11ACC A .…………………………5 分 （2）由（1）知， BD  平面 11ACC A ， 1C D  平面 11ACC A ， 所以 1BD C D .………………………………6 分 在等边 ABC△ 中， 2AB  ，则 1CD  ， 3BD  ， 所以 1 31 32 2BCDS    △ . 又因为 1 1 2 2CC AA  ，所以  2 1 1 2 2 3C D    . 所以 1 1 3 33 32 2BDCS    △ .……………………………………8 分 设点C 到平面 1BDC 的距离为 d ， 由 1 1C BDC C BCDV V 三棱锥 三棱锥 ，得 1 1 1 1 3 3BDC BCDS d S C C    △ △ ， 即 1 3 3 1 3 2 23 2 3 2d     ，解得 2 2 3d  . 即点C 到平面 1BDC 的距离为 2 2 3 .……………………………………12 分 22.【解析】（1）由  xxxf x 2e)( 3  ，得      223e23e2e)( 2323  xxxxxxxf xxx . 令   0f x  ，则   3 2 23 2 2 1 4 2 0x x x x x x        ， 解得 1 2 2x    ， 2 2 2x    ， 3 1x  .……………………………………2 分 当 2 2x    时，   0f x  ，  f x 单调递减； 当 2 2 2 2x      时，   0f x  ，  f x 单调递增； 当 2 2 1x    时，   0f x  ，  f x 单调递减； 高三文数参考答案 第 8 页 共 8 页 当 1x  时，   0f x  ，  f x 单调递增. 综上，函数  f x 的单调递减区间为 , 2 2   ， 2 2,1  ； 单调递增区间为 2 2, 2 2    ， 1, .…………………………5 分 （2）由已知可得      aaxxxaxaxxxf xxx  2323 3e3ee)( .…………………………6 分 因为存在  1 2, 1,3x x  ，使得    1 2f x f x 成立， 所以  f x 在区间  1,3 上存在极值点， 所以   0f x  在区间 1,3 上有解. 所以 3 23 0x x ax a    ，即   3 23 1 31 x xa xx    有解.…………………………9 分 令     3 23 1 31 x xg x xx    ，则 2 2 )1( )33(·2)(   x xxxxg ， 当1 3x  时，   0g x  恒成立， 所以  g x 在 1,3 上单调递增，所以      1 3g g x g  . 又  1 2g  ，   273 2g  ，所以   272 2g x  ， 所以 272 2a  . 即实数 a 的取值范围是 272, 2      .…………………………12 分