2021届新高考版高考数学一轮复习课件：§3-5　对数与对数函数（讲解部分）

2021届新高考版高考数学一轮复习课件：§3-5　对数与对数函数（讲解部分）

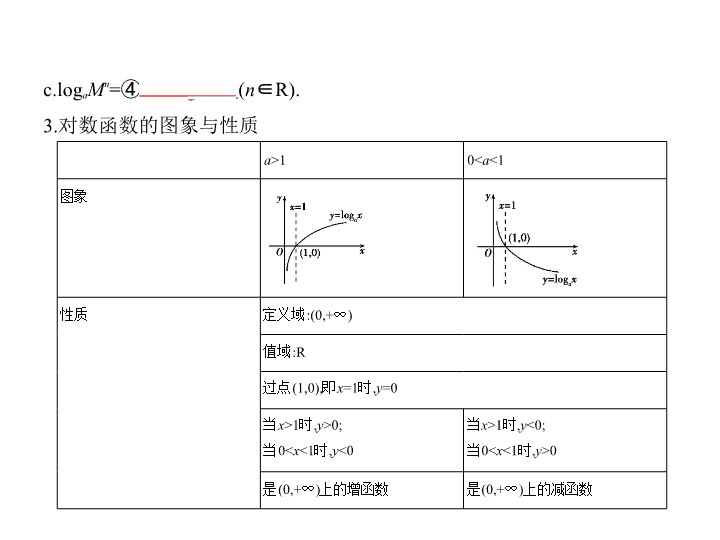
考点　对数与对数函数 1.对数的概念 (1)对数的定义 如果 a x = N ( a >0且 a ≠ 1),那么指数 x 叫做以 a 为底 N 的对数,记作 x =log a N ,其中 a 叫做对数的底数, N 叫做真数. (2)几种常见对数 对数形式 特点 记法 一般对数 底数为 a ( a >0且 a ≠ 1) log a N 常用对数 底数为10 lg N 自然对数 底数为e ln N 考点清单 a.   =①      N       ( a >0且 a ≠ 1, N >0); b.log a a N =②      N      ( a >0且 a ≠ 1). (2)对数的重要公式 a.换底公式:log b N =   ( a , b 均大于零且不等于1, N >0); b.log a b =   ,推广:log a b ·log b c ·log c d =log a d ( a , b , c 均大于零且不等于1, d 大于零); c.lo   M n =   log a M ( a >0且 a ≠ 1, m , n ∈R, m ≠ 0). (3)对数的运算法则 如果 a >0且 a ≠ 1, M >0, N >0,那么 a.log a ( MN )=③     log a M +log a N      ; b.log a   =log a M -log a N ; 2.对数的性质与运算法则 (1)对数的性质 c.log a M n =④      n log a M      ( n ∈R). 3.对数函数的图象与性质 a >1 0< a <1 图象     性质 定义域:(0,+ ∞ ) 值域:R 过点(1,0),即 x =1时, y =0 当 x >1时, y >0; 当0< x <1时, y <0 当 x >1时, y <0; 当0< x <1时, y >0 是(0,+ ∞ )上的增函数 是(0,+ ∞ )上的减函数 4.反函数 指数函数 y = a x ( a >0,且 a ≠ 1)与对数函数 y =log a x ( a >0,且 a ≠ 1)互为反函数,它 们的图象关于直线 y = x 对称.其图象关系如图所示.   考法一　 对数式大小的比较方法 知能拓展 例1 　(1)已知 a =   , b =lo     , c =log 3   ,则   (　　) A. b > c > a 　    B. a > b > c 　    C. c > b > a 　    D. b > a > c (2)设   < a <1, m =log a ( a +1), n =log a (1- a ), p =log a   ,则 m , n , p 的大小关系是   (    ) A. n > m > p 　    B. m > p > n C. p > n > m 　    D. n > p > m 解析 　(1)∵ a =   , b =lo     , c =log 3   ,∴0< a =   <2 0 =1, b =lo     >lo     =1, c = log 3   a > c .故选D. (2)因为   < a <1,所以 a +1-   =   =   >0,   -(1- a )=   =   >0,所以 a +1>   >1- a ,又   < a <1, 所以log a ( a +1)0,且 a ≠ 1)的值域为{ y | y ≥ 1},则函数 y =log a | x |的图象 大致是   (　　) (2)已知 a >0,且 a ≠ 1,函数 f ( x )=log a | ax 2 - x |在[3,4)上是增函数,则 a 的取值范围 是   (　　) A.   ≤ a ≤   或 a >1　    B. a >1 C.   ≤ a <   　    D.   ≤ a ≤   或 a >1 (3)已知函数 f ( x )=log a (8- ax )( a >0,且 a ≠ 1),若 f ( x )>1在区间[1,2]上恒成立,则实 数 a 的取值范围为 　　　     . 解题导引 (1) (2) (3) 解析 　(1)因为函数 y = a | x | ( a >0,且 a ≠ 1)的值域为{ y | y ≥ 1},所以 a >1,故 y =log a | x | 为偶函数且在(0,+ ∞ )上单调递增,故函数 y =log a | x |的大致图象如选项B所示. 故选B. (2)令 y = g ( x )=| ax 2 - x |,由题意知 g ( x ) ≠ 0,作出其图象如下: 函数 f ( x )=log a | ax 2 - x |在[3,4)上是增函数, 若 a >1,则 y =log a x 在(0,+ ∞ )上单调递增,0<   <1,由 g ( x )的图象可知 g ( x )在[3,4) 上递增,故 f ( x )=log a | ax 2 - x |在[3,4)上单调递增,故 a >1时成立;若0< a <1,则   解得   ≤ a ≤   .综上可知, a 的取值范围是   ≤ a ≤   或 a >1. (3)当 a >1时, f ( x )=log a (8- ax )在[1,2]上是减函数,由于 f ( x )>1在[1,2]上恒成立, 所以 f ( x ) min =log a (8-2 a )>1,故8-2 a > a ,即1< a <   ; 当0< a <1时, f ( x )=log a (8- ax )在[1,2]上是增函数,由于 f ( x )>1在[1,2]上恒成立, 所以 f ( x ) min =log a (8- a )>1,且8-2 a >0,所以 a >4,且 a <4,故这样的 a 不存在. 综上可知,实数 a 的取值范围是   . 答案 　(1)B　(2)A　(3)   方法总结　 1.对一些可通过平移、对称作出其图象的对数函数型问题,在 求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合法求解. 2.研究复合函数 y =log a f ( x )的单调性(最值)时,应先研究其定义域,结合函数 u = f ( x )及 y =log a u 的单调性(最值)确定函数 y =log a f ( x )的单调性(最值)(其中 a > 0,且 a ≠ 1).