河南省周口市陈州高级中学2019-2020学年高二下学期第一次周考数学（文）试题

河南省周口市陈州高级中学2019-2020学年高二下学期第一次周考数学（文）试题

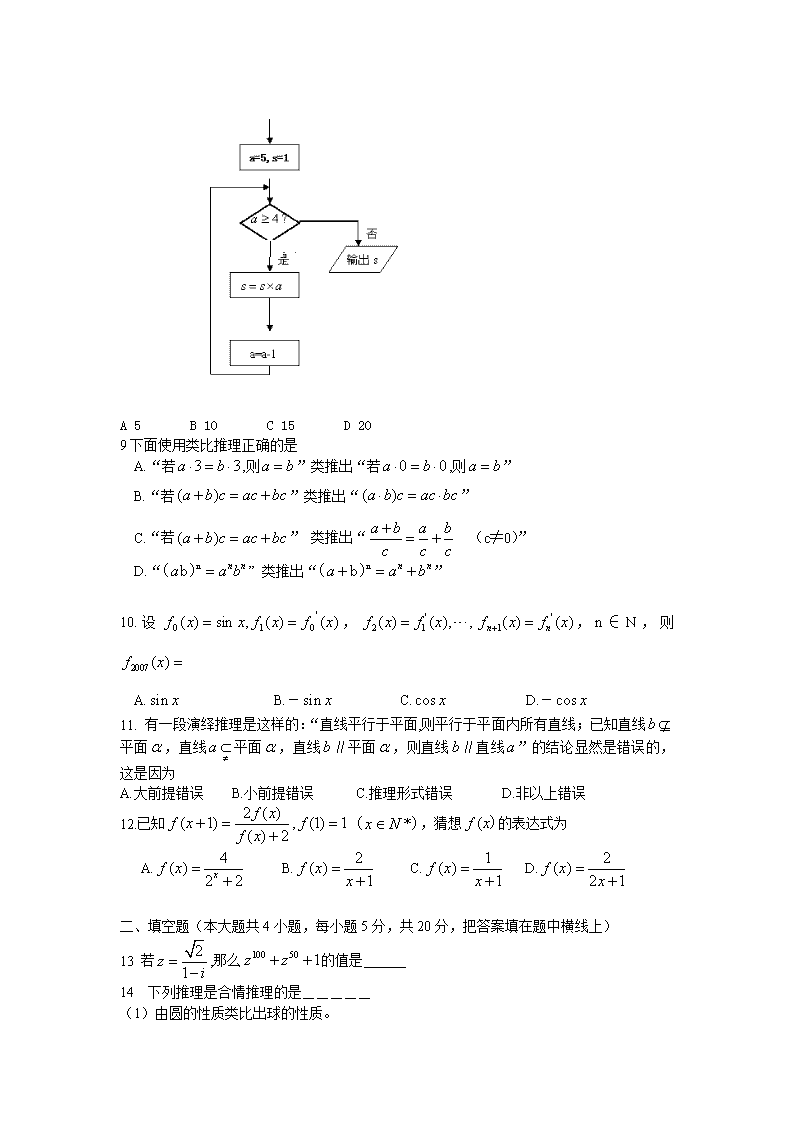
文科数学试题 一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的)‎ ‎1.设有一个回归方程为，变量x增加一个单位时，则( ).‎ A. y平均增加2个单位 B. y平均减少3个单位 C. y平均减少2个单位 D. y平均增加3个单位 ‎2.已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是( )　　A y=1.23x＋4　　　 B y=1.23x+‎5 ‎　　　C y=1.23x+0.08 　　　D y=0.08x+1.23　　‎ ‎3.回归分析中，相关指数R2的值越大，说明残差平方和( )‎ A 越小 　　　B 越大 　　　C 可能大也可能小　　　 D 以上都不对 ‎4．若复数，则在复平面内对应的点位于 ‎ A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 ‎ ‎5.设两个变量x和y之间具有线性相关关系，它们的相关系数是r，y关于x的回归直线的斜率是b，纵截距是a，那么必有（ ）　‎ A b与r的符号相同　　B a与r的符号相同　　C b与r的相反 　D a与r的符号相反 ‎6从甲口袋内摸出1个白球的概率是，从乙口袋内摸出1个白球的概率是，从两个口袋内各摸出1个球，那么等于（ ）‎ ‎2个球都是白球的概率 2个球都不是白球的概率 ‎ ‎2个球不都是白球的概率 2个球中恰好有1个是白球的概率 ‎7.在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）‎ A.若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病;‎ B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病;‎ C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推断出现错误;‎ D.以上三种说法都不正确.‎ ‎8.在如图的程序图中，输出结果是（ ）　　　‎ ‎　　　　　　　　　　　‎ A 5 　　　B ‎10 ‎　　　C 15 　　　D 20‎ ‎9下面使用类比推理正确的是 ‎ A.“若,则”类推出“若,则”‎ B.“若”类推出“”‎ C.“若” 类推出“ （c≠0）”‎ D.“” 类推出“”‎ ‎ ‎ ‎10.设，，n∈N，则 ‎ A. B.－ C. D.－‎ ‎11. 有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线平面，直线平面，直线∥平面，则直线∥直线”的结论显然是错误的，这是因为 ‎ A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 ‎12.已知 ，猜想的表达式为 ‎ A. B. C. D.‎ 二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）‎ ‎13 若,那么的值是 ‎ ‎14 下列推理是合情推理的是＿＿＿＿＿‎ ‎（1）由圆的性质类比出球的性质。‎ ‎（2）由直角三角形、等腰三角形、等边三角形的内角和是 ‎，推出所有三角形的内角和是。‎ ‎（3）则。‎ ‎（4）三角形的内角和是，四边形的内角和是，五边形的内角和是，由此推出n边形的内角和是。‎ ‎15.袋中有6个黄色、4个白色的乒乓球，作不放回抽样，每次任取一球，取2次，其中一个是黄色的，求另一个也是黄色的概率为 16.设平面内有ｎ条直线，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用表示这ｎ条直线交点的个数，当ｎ＞４时，＝ ‎ ‎（用含n的数学表达式表示）‎ ‎ ‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）‎ ‎17(本小题满分10分)‎ 在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲.‎ ‎（1）根据以上的数据建立一个2×2的列联表；‎ ‎（2）若认为“性别与患色盲有关系”，则有多少把握？‎ ‎18（本小题满分12）‎ 假设关于某设备的使用年限的所支出的维修费用（万元）有如下的统计数据：‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2．2‎ ‎3．8‎ ‎5．5‎ ‎6．5‎ ‎7．0‎ 若由此资料知与呈线性关系，试求：‎ ‎（1）回归直线方程；‎ ‎（2）估计使用年限为10年时，维修费用为多少？‎ ‎19．（本小题满分12）已知，且，求证：．‎ ‎20. （本小题满分12）已知复数满足: 求的值 ‎ ‎21．（本小题满分12）△ABC三边长的倒数成等差数列，求证：角.‎ ‎22. （本小题满分12分）‎ 甲、乙两人各进行一次射击如果两人击中目标的概率都是0.6。计算 ‎（1）两人都击中目标的概率；‎ ‎（2）其中恰有一人击中目标的概率；‎ ‎（3）至少有一人击中目标的概率；‎ ‎ ‎ 高二文科数学试题（参考答案）‎ ‎ 一、选择题 ‎1． 2． 3． 4． 5． 6． 7． 8． 9． 10． 11． 12． ‎ 二、填空题　　‎ ‎13. . i ‎14.（1）（2）（4）‎ ‎15. 16. ‎ 三、解答题 ‎17．解析：‎ ‎（1）‎ ‎　‎ 患色盲 不患色盲 总计 男 ‎38‎ ‎442‎ ‎480‎ 女 ‎6‎ ‎514‎ ‎520‎ 总计 ‎44‎ ‎956‎ ‎1000‎ ‎（2）‎ ‎27.14＞6.635 ．若认为“性别与患色盲有关系”，则有99％的把握 　18．解析：‎ ‎（1）由表格知：‎ 于是，‎ ‎ ‎ 所以所求回归直线方程为 ‎（2）当时，‎ 估计使用年限为10年时，维修费用12．38万元　　‎ ‎19. 证明：(分析法)因为，且，‎ 所以，，要证明原不等式成立，只需证明，‎ 即证，从而只需证明，‎ 即，因为，，‎ 所以成立，故原不等式成立．‎ ‎20．设，而即 则 ‎21（方法一）.证明：=‎ 为△ABC三边，， .‎ ‎（方法二）反证法 ‎ ‎ ‎22解：（1）“两人各射击一次，都击中目标”就是事件AB发生，因此所求概率为 P（ AB ）=P（A）P（B）=0.6×0.6=0.36‎ ‎（2）分析：“两人各射击一次，恰有一人击中目标”包括两种情况：甲击中，乙未击中（事件AB发生）；甲未击中，乙击中（事件AB发生）。‎ 因此所求概率为 ‎。‎ ‎（3）分析：“两人各射击一次，至少有一人击中目标”包括三种情况：甲击中，乙未击中（事件AB发生）；甲未击中，乙击中（事件AB发生）；甲、乙两人都击中目标（事件AB发生）‎ 解法一：“两人各射击一次，至少有一人击中目标”的概率为 P=P(AB) ＋P(AB) ＋P(AB) =0.6×0.6 ＋ 0.6×(1－0.6) ＋(1－0.6) ×0.6‎ ‎ =0.36 ＋0.48 =0.84‎ 方法二：分析：“两人都未击中目标（事件AB发生）”的概率为 P（A·B）=P（A） · P（B）=(1－0.6) ×(1－0.6)=0.16‎ P=1－P（AB）=1－0.16=0.84‎