2017-2018学年安徽省合肥市重点中学高二下学期期末考试数学（文）试题（Word版）

2017-2018学年安徽省合肥市重点中学高二下学期期末考试数学（文）试题（Word版）

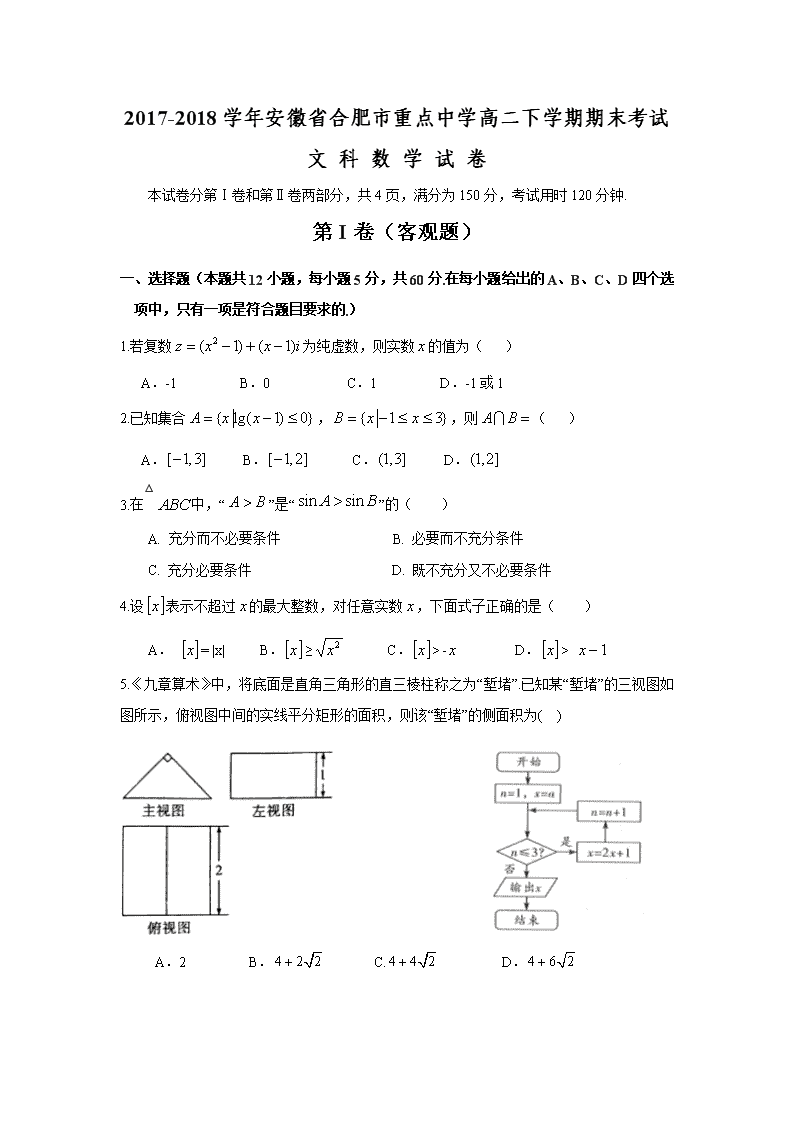
‎2017-2018学年安徽省合肥市重点中学高二下学期期末考试 文 科 数 学 试 卷 本试卷分第Ⅰ卷和第Ⅱ卷两部分，共4页，满分为150分，考试用时120分钟.‎ 第I卷（客观题）‎ 一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的A、B、C、D四个选项中，只有一项是符合题目要求的.）‎ ‎1.若复数为纯虚数，则实数的值为（ ）‎ ‎ A．-1 B．‎0 ‎ C．1 D．-1或1‎ ‎2.已知集合，，则（ ）‎ ‎ A． B． C． D．‎ ‎3.在△中，“”是“”的（ ）‎ ‎ A. 充分而不必要条件 B. 必要而不充分条件 ‎ ‎ C. 充分必要条件 D. 既不充分又不必要条件 ‎4.设表示不超过的最大整数，对任意实数，下面式子正确的是（ ）‎ ‎ A． = |x| B．≥ C．> D．> ‎ ‎5.《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示，俯视图中间的实线平分矩形的面积，则该“堑堵”的侧面积为( )‎ ‎ A．2 B． C. D．‎ ‎6.已知各项均为正数的等比数列,满足,且，则公比（ ）‎ A. B. C. D. ‎ ‎7.定义在上的奇函数满足,当时, ,则 A. B. C. D. ‎ ‎8.函数的零点所在区间为（ ）‎ A. B. C. D. ‎ ‎9.已知是定义在上的奇函数，且则= （ ）‎ A. B. C. D. ‎ ‎10..已知是定义在上的奇函数，当时，，则不等式的解集为（ ）‎ A． B． C． D．‎ ‎11..函数的图象大致是（ ）‎ A． B．‎ C． D．‎ ‎12.已知对任意，不等式恒成立(其中是自然对数的底数），则实数的取值范围是（ ）‎ A． B． C． D．‎ 第II卷（主观题）‎ 二、填空题（本题共4个小题，每小题5分，共20分.请把答案填在答题纸的指定位置）‎ ‎13.已知函数是的导函数，则 .‎ 14. ‎ .‎ ‎15.函数有极值点，则实数的取值范围为 .‎ ‎16.设函数则满足的的取值范围是__________.‎ 三、解答题（本题共6个小题，满分70分）‎ ‎17.（本小题满分10分）‎ 等比数列的前项和为，公比为，若，且 （1） 求的通项公式；‎ （2） 求数列的前项和为.‎ ‎18.（本小题满分12分）‎ 设为数列的前项和，已知.‎ ‎（1）求的通项公式 ‎（2）已知，求的前项和.‎ ‎19.（本小题满分12分）‎ 设函数，若函数的图像在处与直线相切.‎ ‎（1）求实数的值；‎ ‎（2）求函数在上的最大值.‎ ‎20.（本小题满分12分）‎ 设为数列的前项和，已知，．‎ ‎（1）证明：为等比数列；‎ ‎（2）求的通项公式，并判断，，是否成等差数列？‎ ‎21.（本小题满分12分）‎ 已知函数．‎ ‎（1）求曲线在处的切线方程；‎ ‎（2）设，若有两个零点，求实数的取值范围．‎ ‎22.（本小题满分12分）‎ 已知函数．‎ ‎（1）若为的极值点，求的单调区间；‎ ‎（2）当时，，求的取值范围．‎ ‎．‎ ‎【答案】‎ ‎1-5: ADCDC ‎6-10:ABCCA;‎ ‎11.A 12.A ‎13.e ‎14.‎ 14. 15. 16. ‎(1) ‎ ‎ (2) ‎ ‎ 18.(1) ‎ ‎ (2) ‎ ‎ 19.（1） ‎ 因为函数的图像在处与直线相切 所以；‎ 解得 ‎（2）由（1）得，，解得（舍）‎ ‎1‎ ‎+‎ ‎0‎ 增 极大 减 ‎20.(1)∵，，∴，‎ ‎∴，∴，，‎ 又，，‎ ‎∴是首项为2公比为2的等比数列．‎ ‎（2）解：由（1）知，，∴，‎ ‎∴，‎ ‎∴，∴，‎ 即，，成等差数列．‎ ‎21.（1）由题易知，，‎ ‎，在处的切线方程为．‎ ‎（2）由题易知，．‎ 当时，，在上单调递增，不符合题意．‎ 当时，令，得，在上，，在上，，‎ 在上单调递减，在上单调递增，‎ ‎．‎ 有两个零点，，即，‎ ‎∵，∴，解得，‎ ‎∴实数的取值范围为．‎ ‎22.（1），因为为的极值点，所以 所以，．‎ 令，得；令，得．‎ ‎∴的单调递减区间为，单调递增区间为．‎ ‎（2）当时，在上单调递减，∴，不合题意．‎ 当时，，不合题意．‎ 当时，，在上单调递增，‎ ‎∴，故满足题意．‎ 当时，在上单调递减，在单调递增，‎ ‎∴，故不满足题意．‎