- 2021-07-01 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届安徽省马鞍山市二中高二上学期期中素质测试(2016-11)
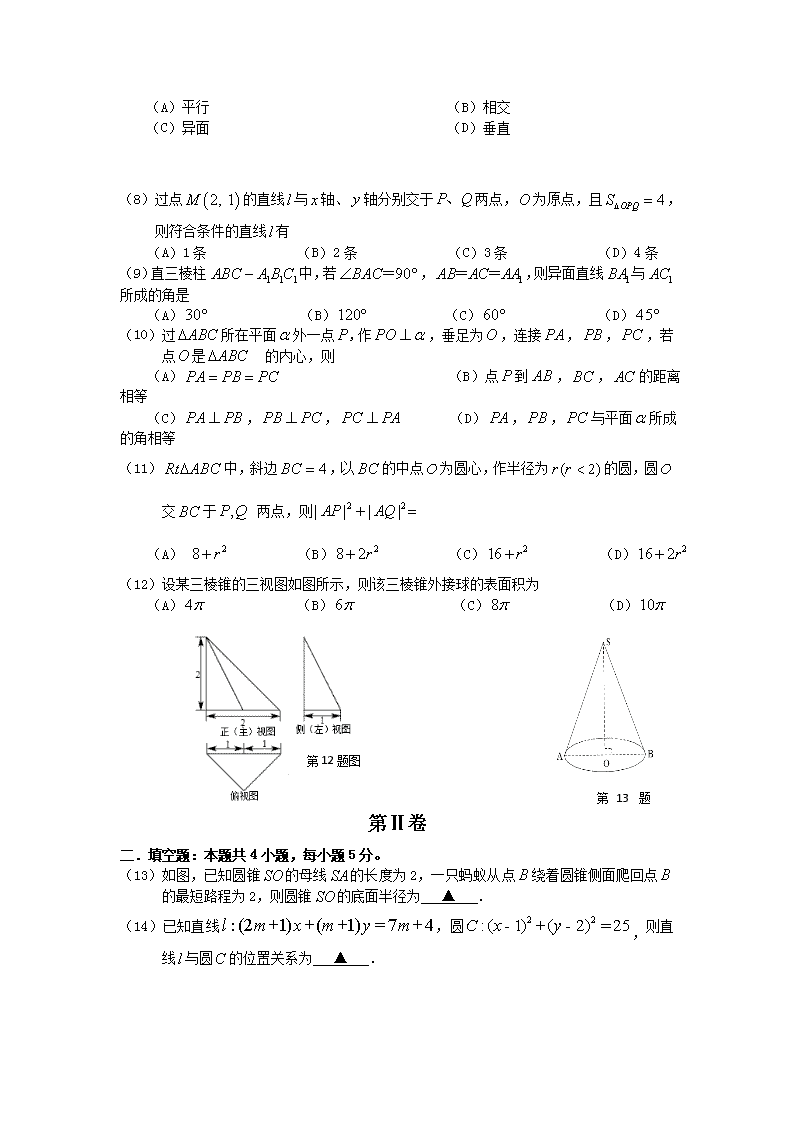
马鞍山市第二中学2016—2017学年度第一学期期中素质测试 高二数学(文科) 第Ⅰ卷 一、选择题:本题共12小题,每小题5分, 在每小题给出的四个选项中,只有一项是符合题目要求的。 (1)直线的倾斜角是 (A) (B) (C) (D) (2)在空间直角坐标系中,点关于平面对称点的坐标是 (A) (B) (C) (D) (3)下列能得出平面平面的一个条件是 (A)存在一条直线 (B)存在一条直线 (C)存在两条平行直线 (D)存在两条异面直线 (4)经过两点,的直线方程都可以表示为 (A) (B) (C) (D) (5)已知平面,及直线满足,,,,则 (A) (B) (C) (D)与相交但不垂直 (6)圆关于直线 对称的圆的方程是 (A) (B) (C) (D) (7)已知:空间四边形如图所示,分别是的中点,第7题图 分别是,上的 点,且.,则直线与直线 (A)平行 (B)相交 (C)异面 (D)垂直 (8)过点的直线与轴、轴分别交于两点,为原点,且,则符合条件的直线有 (A)1条 (B)2条 (C)3条 (D)4条 (9)直三棱柱中,若,,则异面直线与所成的角是 (A) (B) (C) (D) (10)过所在平面外一点,作,垂足为,连接,,,若点是 的内心,则 (A) (B)点到,,的距离相等 (C),, (D),,与平面所成的角相等 (11)中,斜边,以的中点为圆心,作半径为的圆,圆交于 两点,则 (A) (B) (C) (D) (12)设某三棱锥的三视图如图所示,则该三棱锥外接球的表面积为 (A) (B) (C) (D) 第12题图 第13题图 第Ⅱ卷 二.填空题:本题共4小题,每小题5分。 (13)如图,已知圆锥的母线的长度为2,一只蚂蚁从点绕着圆锥侧面爬回点的最短路程为2,则圆锥的底面半径为 ▲ . (14)已知直线,圆,则直线与圆的位置关系为 ▲ . (15)点满足,则的取值范围为 ▲ . (16)在平行四边形中,,将它沿对角线折起,使得与 成角,则间的距离为 ▲ . 三、解答题(请在答题卷上写出文字说明,证明过程或演算步骤) (17)(本小题满分10分) 已知四棱锥,其三视图和直观图如图所示,为中点. (Ⅰ)求此几何体的体积; (Ⅱ)求证:平面平面. (18)(本小题满分12分) 已知圆的方程为:. (Ⅰ)试求的值,使圆的面积最小; (Ⅱ)求与满足(1)中条件的圆相切,且过点的直线方程. (19)(本小题满分12分) 已知空间几何体中,四边形是正方形,平面,平面,. (Ⅰ)求证:∥平面; F (Ⅱ)求与平面所成角的正弦值. E A D C B (20)(本小题满分12分) 设直线的方程为. (Ⅰ)若直线在两坐标轴的截距相等,求直线的方程; (Ⅱ)若直线不经过第二象限,求实数的取值范围. (21)(本小题满分12分) 如图,在空间几何体中,底面是梯形,且∥, 是边长为的等边三角形,为的中点. (Ⅰ)求证:平面⊥平面; (Ⅱ)求几何体的体积. (22)(本小题满分12分) 已知圆的圆心在坐标原点且与直线相切. (Ⅰ)求直线被圆所截的弦的长; (Ⅱ)过点作两条与圆C相切的直线,切点分别为,求直线的方程; (Ⅲ)若与直线垂直的直线与圆C交于不同的两点,且为钝角,求直线在轴上的截距的取值范围. 马鞍山市第二中学2016—2017学年度 高二第一学期期中素质考试数学(文科)答案 一.选择题:本题共12小题,每小题5分 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A D C B B B C C B B C 二、填空:本题共4小题,每小题5分 13. 14.相交 15. 16. 三、解答题: 17. 解:(1)由三视图可知底面ABCD为矩形,定点P在面ABCD内的射影为BC的中点E,棱锥的高为2 ……………………………………4分 (2)平面,平面,, 取中点,, ,, ,平面, 平面, 平面平面 ……………………………………10分 18. 解:圆的方程为: (1)当时,圆的半径有最小值,此时圆的面积最小 ……………………………………4分 (2)当时,圆的方程为 设所求的直线为,即 , 当与轴垂直时,也满足条件。 ……………………………………12分 19.(1)证明:取AF的中点G连结BG,GD,EG 平面,平面,且, 四边形为平行四边形,, 同理可证四边形为平行四边形,且, 又且,且, 四边形为平行四边形,且, 又, 平面平面,平面 ……………………………………6分 (2)设,则, 连结,易证平面, 为与平面所成角的平面角, 在中, ……………………………………12分 20. 解:(1)当时,显然不满足题意 在轴上的截距是,在轴上的截距是 解得 直线的方程为 ……………………………………6分 (2)直线可化为: 由已知 ……………………………………12分 21. 证明:(1)取的中点,连 , 为等边三角形, ,且, 在中,, ,,即, ,平面, 平面,平面 ……………………………………6分 , 是中点, ……………………………………12分 22.解:(1)由已知,,则圆C的方程为 ……………………………………4分 (2) 连OG,OM.则 ……………………………………8分 (3)设所求直线的方程为:,点, 由可得,则, 由得;由为钝角, 即; 与共线时,,. ……………………………………12分查看更多