人教A数学必修一对数函数及其性质

人教A数学必修一对数函数及其性质

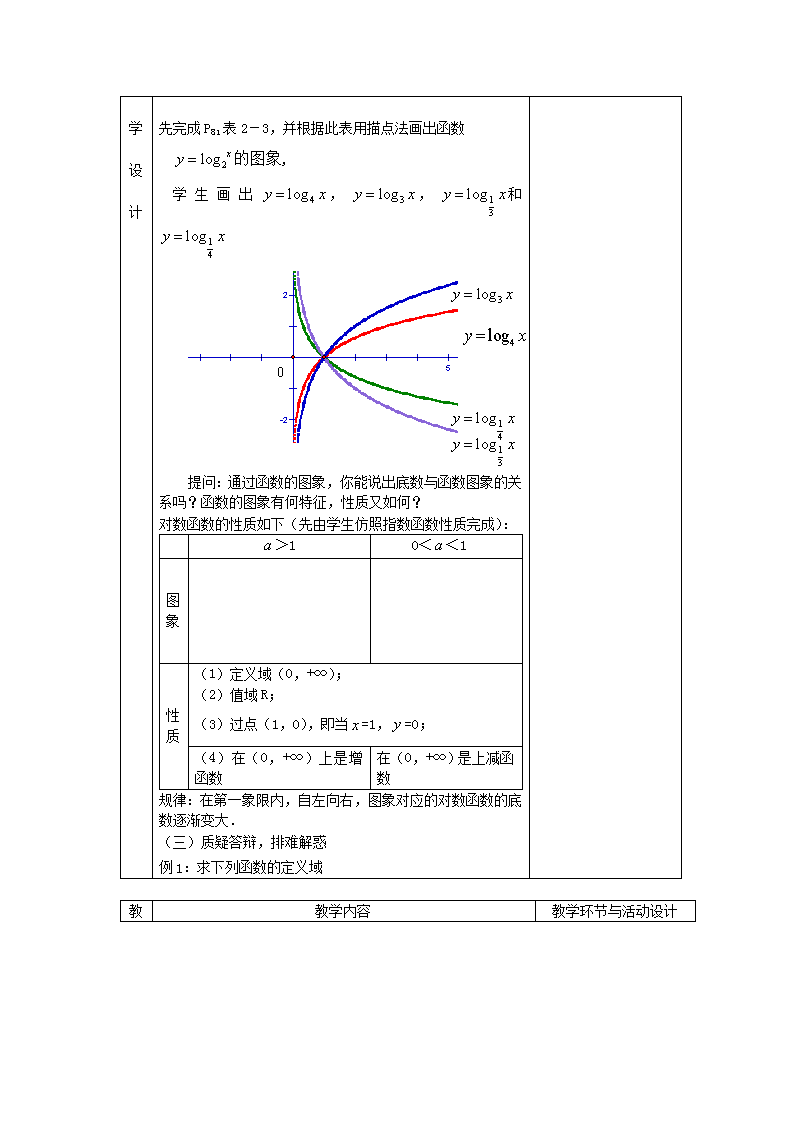
河北武邑中学课堂教学设计 备课人 授课时间 课题 ‎§‎2.2.2‎对数函数及其性质（1）‎ 教 学 目 标 知识与技能 理解对数函数的概念，掌握对数函数的图像和性质；会利用对数函数的图像和性质解决相关的数学问题 过程与方法 启发引导，充分发挥学生的主体作用 情感态度价值观 能借助计算器或计算机画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点 重点 对数函数的概念、图象和性质.‎ 难点 如何从对数函数的图像归纳出对数函数的性质 教 学 设 计 教学内容 教学环节与活动设计 ‎（一）创设情景，揭示课题 在2．2．1的例6中，考古学家利用估算出土文物或古遗址的年代，对于每一个C14含量P，通过关系式，都有唯一确定的年代与之对应．同理，对于每一个对数式中的，任取一个正的实数值，均有唯一的值与之对应，所以的函数．‎ ‎（二）研探新知 一般地，我们把函数（＞0且≠1）叫做对数函数，其中是自变量，函数的定义域是（0，+∞）．‎ 提问：（1）．在函数的定义中，为什么要限定＞0且≠1．‎ ‎（2）．为什么对数函数（＞0且≠1）的定义域是（0，+∞）．‎ 注意： 对数函数的定义与指数函数类似，都是形式定义，注意辨别．如：， 都不是对数函数，而只能称其为对数型函数．‎ 下面我们来研究函数的图象，并通过图象来研究函数的性质：‎ 教师组织学生充分讨论、交流，使学生更加理解对数函数的含义，从而加深对对数函数的理解.‎ 教 教学内容 教学环节与活动设计 学 设 计 ‎ ‎ 先完成P81表2－3，并根据此表用描点法画出函数 学生画出，，和 ‎0‎ 提问：通过函数的图象，你能说出底数与函数图象的关系吗？函数的图象有何特征，性质又如何？‎ 对数函数的性质如下（先由学生仿照指数函数性质完成）：‎ ‎＞1‎ ‎0＜＜1‎ 图 象 性 质 ‎（1）定义域（0，+∞）；‎ ‎（2）值域R；‎ ‎（3）过点（1，0），即当=1，=0；‎ ‎（4）在（0，+∞）上是增函数 在（0，+∞）是上减函数 规律：在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大．‎ ‎（三）质疑答辩，排难解惑 例1：求下列函数的定义域 ‎（1） （2） （＞0且≠1）‎ 教 教学内容 教学环节与活动设计 学 设 计 例2. 比较下列各组数中的两个值大小 ‎（1） ‎ ‎（2）‎ ‎（3） （＞0，且≠1）‎ 小结：分类讨论的思想．‎ 对数函数的单调性取决于对数的底数是大于1还是小于1．而已知条件并未指明，因此需要对底数a进行讨论，体现了分类讨论的思想，要求学生逐步掌握．‎ 课堂练习：（课本第73页练习2、3）‎ 教 学 小 结 对数函数的概念、图像和性质 课后 反思