甘肃省武威市第十八中学2019-2020学年高二下学期期中考试数学（文）试题

甘肃省武威市第十八中学2019-2020学年高二下学期期中考试数学（文）试题

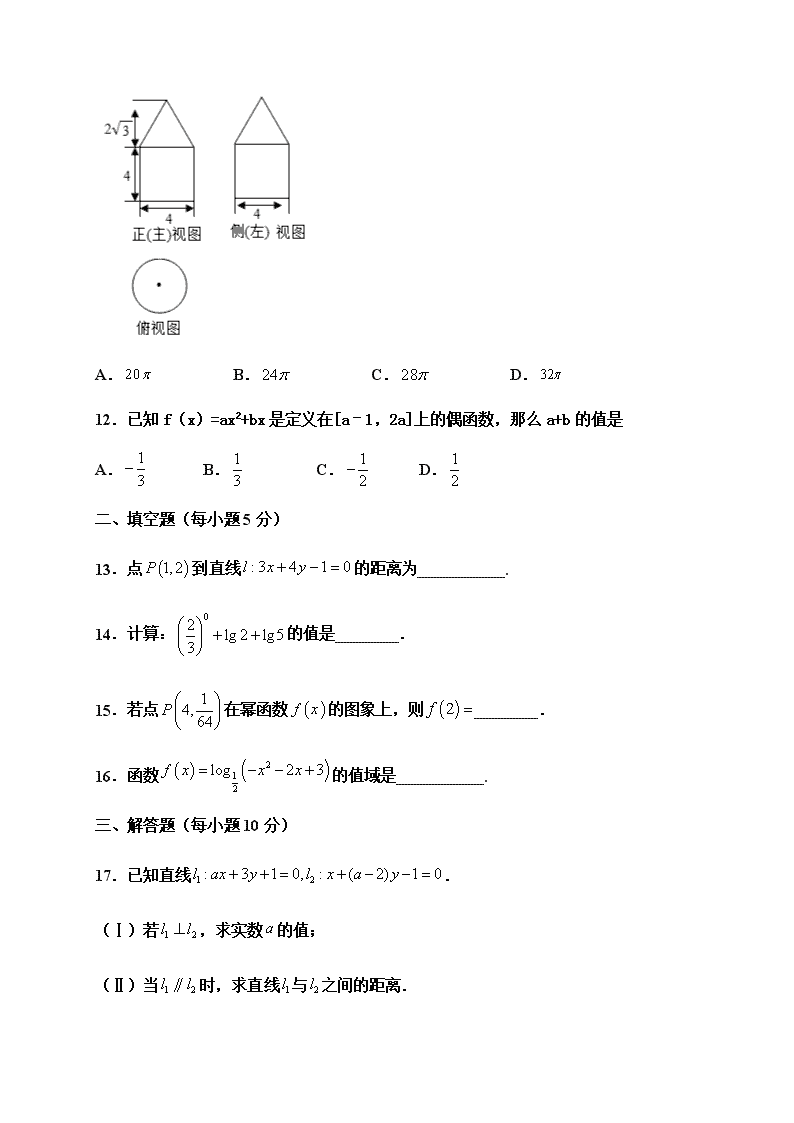
‎2019—2020学年第二学期期中考试试题 高二文科数学 一、选择题（每小题5分）‎ ‎1．设全集为，集合，，则（ ）‎ A． B． C． D．‎ ‎2．若是互不相同的空间直线，是不重合的平面，则下列命题中真命题是( )‎ A．若则 B．若 则 C．若，，则 D．若，，则 ‎3．下列函数中，与相等的为（ ）‎ A． B． C． D．‎ ‎4．函数的图像大致是（ ）‎ A． B． C． D．‎ ‎5．已知函数，则（ ）‎ A．1 B．2 C．3 D．6‎ ‎6．华罗庚是上世纪我国伟大的数学家，以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.‎ 他除了数学理论研究，还在生产一线大力推广了“优选法”和“统筹法”.“优选法”，是指研究如何用较少的试验次数，迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻，为防范机场带来的境外输入，某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率：每16人为组，把每个人抽取的鼻咽拭子分泌物混合检查，如果为阴性则全部放行；若为阳性，则对该16人再次抽检确认感染者.某组16人中恰有一人感染（鼻咽拭子样本检验将会是阳性），若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组，选其中一组8人的样本混合检查，若为阴性则认定在另一组；若为阳性，则认定在本组.继续把认定的这组的8人均分两组，选其中一组4人的样本混合检查……以此类推，最终从这16人中认定那名感染者需要经过（ ）次检测.‎ A．3 B．4 C．6 D．7‎ ‎7．的零点所在的区间是（ ）‎ A． B． C． D．‎ ‎8．已知，，，则（ ）‎ A． B． C． D．‎ ‎9．函数的定义域是（ ）‎ A． B． C． D．‎ ‎10.若复数(a2－3a＋2)＋(a－1)i是纯虚数，则实数a的值为(　　)‎ A．1 B．2 C．1或2 D．－1‎ ‎11．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎12．已知f（x）=ax2+bx是定义在[a–1，2a]上的偶函数，那么a+b的值是 A． B． C． D．‎ 二、填空题（每小题5分）‎ ‎13．点到直线的距离为___________.‎ ‎14．计算：的值是________．‎ ‎15．若点在幂函数的图象上，则________．‎ ‎16．函数的值域是___________.‎ 三、解答题（每小题10分）‎ ‎17．已知直线．‎ ‎（Ⅰ）若，求实数的值；‎ ‎（Ⅱ）当时，求直线与之间的距离．‎ ‎18．已知函数.‎ ‎（1）若函数是偶函数，且，求的解析式；‎ ‎（2）在（1）的条件下，求函数在上的最大、最小值；‎ ‎（3）要使函数在上是单调函数，求的范围.‎ ‎19．如图所示，在三棱柱中，与都为正三角形，且平面，分别是的中点.‎ 求证：（1）平面平面；‎ ‎（2）平面平面.‎ ‎20．已知直线的参数方程为（t为参数），曲线C的参数方程为（θ为参数）.‎ ‎⑴将曲线C的参数方程化为普通方程；‎ ‎⑵若直线l与曲线C交于A、B两点，求线段AB的长.‎ 高二数学文科答案 一、选择题（共12小题，每小题5分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ D C C A B B B B A B C B 二、 填空题（共4小题，每小题5分）‎ ‎13、2 ； 14、2 ； 15、 ； 16、.‎ 三、 解答题 17. ‎（10分）‎ ‎ （Ⅰ）∵，且，‎ ‎∴，解得．‎ ‎（Ⅱ）∵，且，‎ ‎∴且，解得，‎ ‎∴，即 ‎∴直线间的距离为． ‎ 17. ‎（10分）‎ ‎（1）函数是偶函数，所以恒成立，‎ 恒成立，，‎ ‎，‎ ‎（2）由（1），当时，取得最小值为，‎ 当时，取得最大值为；‎ ‎（3）对称轴为，‎ 要使函数在上是单调函数，‎ 需或，解得或.‎ 所以的范围是或.‎ ‎19（10分） ‎ ‎（1）在三棱柱中，‎ 因为分别是的中点，所以，‎ 根据线面平行的判定定理，可得平面，平面 又，‎ ‎∴平面平面.‎ ‎（2）在三棱柱中，平面，所以，‎ 又，，所以平面，‎ 而平面，所以平面平面.‎ ‎20（10分）‎ 解答：⑴…………5分 ‎⑵将代入，并整理得 设A，B对应的参数为，，则，‎ ‎…………10分