高中数学（人教A版）必修4：2-2-3同步试题（含详解）

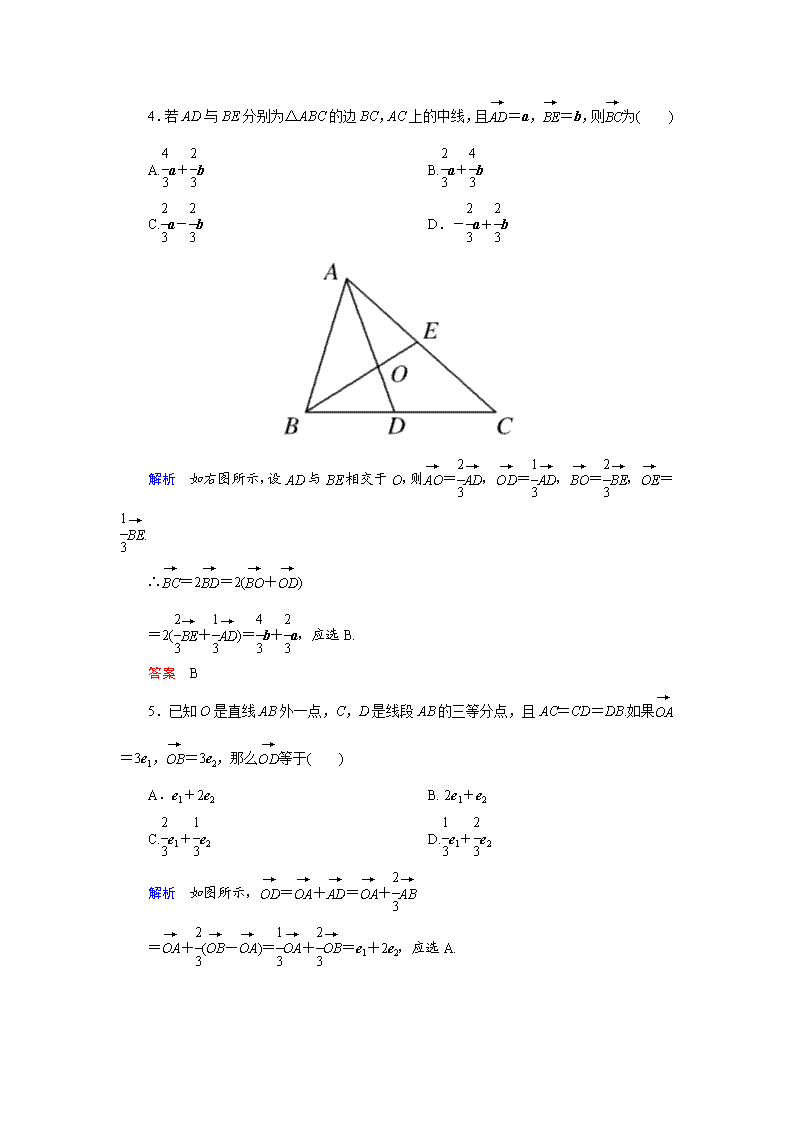
高中数学（人教A版）必修4：2-2-3同步试题（含详解）

高中数学(人教A版)必修4同步试题 ‎1．给出下列四个结论 ‎①－＝；‎ ‎②0(a)＝0；‎ ‎③0(0)＝0；‎ ‎④若两个非零向量a，b满足a＝kb(k≠0)，则a，b方向相同．‎ 其中正确结论的个数是(　　)‎ A．0　　　　　　　　　　 B．1‎ C．2 D．3‎ 解析　①－＝，∴①错．②0(a)＝0，∴②错．‎ ‎③0(0)＝0正确．④a与b共线，方向可能相同，也可能相反，∴④错．因此正确的只有③，应选B.‎ 答案　B ‎2．下列叙述不正确的是(　　)‎ A．若a，b共线，则存在唯一的实数λ，使a＝λb.‎ B. b＝‎3a(a为非零向量)，则a，b共线 C．若m＝‎3a＋4b，n＝a＋2b，则m∥n D．若a＋b＋c＝0，则a＋b＝－c 解析　判断a与b共线的方法是：存在实数λ，使a＝λb.在A中，若b＝0时不成立．B正确．在C中，m＝2n，∴m∥n，∴C正确．D也正确，所以应选A.‎ 答案　A ‎3．下列说法不正确的是(　　)‎ A．若＝，则A，O，B三点共线 B．若＝，则∥ C．若|λa|＝|λ||a|(λ∈R)，则λa与a方向相同 D．若a＝‎4m＋n，b＝m＋n则a－b＝‎‎3m 解析　A、B、D正确，C错．应选C.‎ 答案　C ‎4．若AD与BE分别为△ABC的边BC，AC上的中线，且＝a，＝b，则为(　　)‎ A.a＋b　　　　　　　 B.a＋b C.a－b D．－a＋b 解析　如右图所示，设AD与BE相交于O，则＝，＝，＝，＝.‎ ‎∴＝2＝2(＋)‎ ‎＝2(＋)＝b＋a，应选B.‎ 答案　B ‎5．已知O是直线AB外一点，C，D是线段AB的三等分点，且AC＝CD＝DB.如果＝3e1，＝3e2，那么等于(　　)‎ A．e1＋2e2 B. 2e1＋e2‎ C.e1＋e2 D.e1＋e2‎ 解析　如图所示，＝＋＝＋ ‎＝＋(－)＝＋＝e1＋2e2，应选A.‎ 答案　A ‎6．已知|a|＝4，b与a的方向相反，且|b|＝2，a＝mb，则实数m＝________.‎ 答案　－2‎ ‎7．若a，b为已知向量，且(‎4a－‎3c)＋3(‎5c－4b)＝0，则c＝________.‎ 解析　(‎4a－‎3c)＋3(‎5c－4b)＝0，‎ a－‎2c＋‎15c－12b＝0，‎ ‎∴‎13c＝12b－a，‎ ‎∴c＝b－a.‎ 答案　b－a ‎8．有下面四个命题：‎ ‎①对于实数m和向量a，b，恒有m(a－b)＝ma－mb；‎ ‎②对于实数m，n和向量a，恒有(m－n)a＝ma－na；‎ ‎③对于实数m和向量a，b，若ma＝mb，则a＝b；‎ ‎④对于实数m，n和非零向量a，若ma＝na，则m＝n.‎ 其中真命题有________．‎ 解析　由实数与向量积的运算知，①、②、④正确．‎ 答案　①②④‎ ‎9．如图所示，在△OAB中，延长BA到C，使AC＝BA，在OB上取点D，使DB＝OB.DC与OA交于E，设＝a，＝b，用a，b表示向量，.‎ 解　因为A是BC的中点，所以＝(＋)，即＝2－＝‎2a－b.‎ ＝－＝－＝‎2a－b－b＝‎2a－b.‎ ‎10．已知：＝3，＝3，且B，C，D，E不共线．‎ 求证：BC∥DE.‎ 证明　∵＝3，＝3，‎ ‎∴＝－＝3－3 ‎＝3(－)＝3.‎ ‎∴与共线．‎ 又∵B，C，D，E不共线．‎ ‎∴BC∥DE.‎ 教师备课资源 ‎1.若5＋3＝0，且||＝||，则四边形ABCD是(　　)‎ A．平行四边形 B．菱形 C．矩形 D．等腰梯形 解析　由于5＋3＝0知，∥且||≠||，∴此四边形为梯形．又||＝||，∴梯形ABCD为等腰梯形．‎ 答案　D ‎2．点P是△ABC所在平面内一点，若＝λ＋，其中λ∈R，则点P一定在(　　)‎ A．△ABC的内部 B．AC边所在的直线上 C．AB边所在的直线上 D．BC边所在的直线上 解析　∵＝λ＋，‎ ‎∴－＝λ，‎ 即＋＝λ.‎ ‎∴＝λ.‎ ‎∴C，P，A三点共线．‎ ‎∴点P在AC边所在的直线上．‎ 答案　B ‎3．已知向量a，b不共线，实数x，y满足5xa＋(8－y)b＝4xb＋3(y＋9)a，求x，y.‎ 解　∵a与b不共线，根据向量相等得 解得 ‎∴x＝3，y＝－4.‎ ‎4．已知O是△ABC所在平面内一点，D为BC边的中点，且2＋＋＝0，那么(　　)‎ A.＝ B.＝2 C.＝3 D．2＝ 解析　∵2＋＋＝0，而＋＝2，∴2＋2＝0，即＋＝0，∴＝.‎ 答案　A ‎5．已知非零向量a，b，c满足a＋b＋c＝0，则表示a，b，c的有向线段能否一定构成三角形？‎ 错解　在平面内任取一点A，作＝a，再以B为起点作＝b，则由向量的三角形法则知，＝a＋b，又a＋b＋c＝0，∴c＝－(a＋b)＝－＝.因此，当a＋b＋c＝0时，表示a，b，‎ c的有向线段一定能构成三角形．‎ 错因分析　上述解法只考虑了一般情况，而忽视了向量共线的特殊情况．‎ 正解　(1)当a，b不共线时，即为上述解法，这时表示a，b，c的有向线段一定能构成三角形．‎ ‎(2)当a，b共线时，由a＋b＋c＝0知，c＝－(a＋b)．显然c也与a，b共线，这时表示a，b，c的有向线段不能构成三角形．‎ 综上知，若非零向量a，b，c满足a＋b＋c＝0，则表示a，b，c的有向线段不一定能构成三角形．‎