数学理卷·2018届河北省临漳县第一中学高三上学期第二次月考（2017

数学理卷·2018届河北省临漳县第一中学高三上学期第二次月考（2017

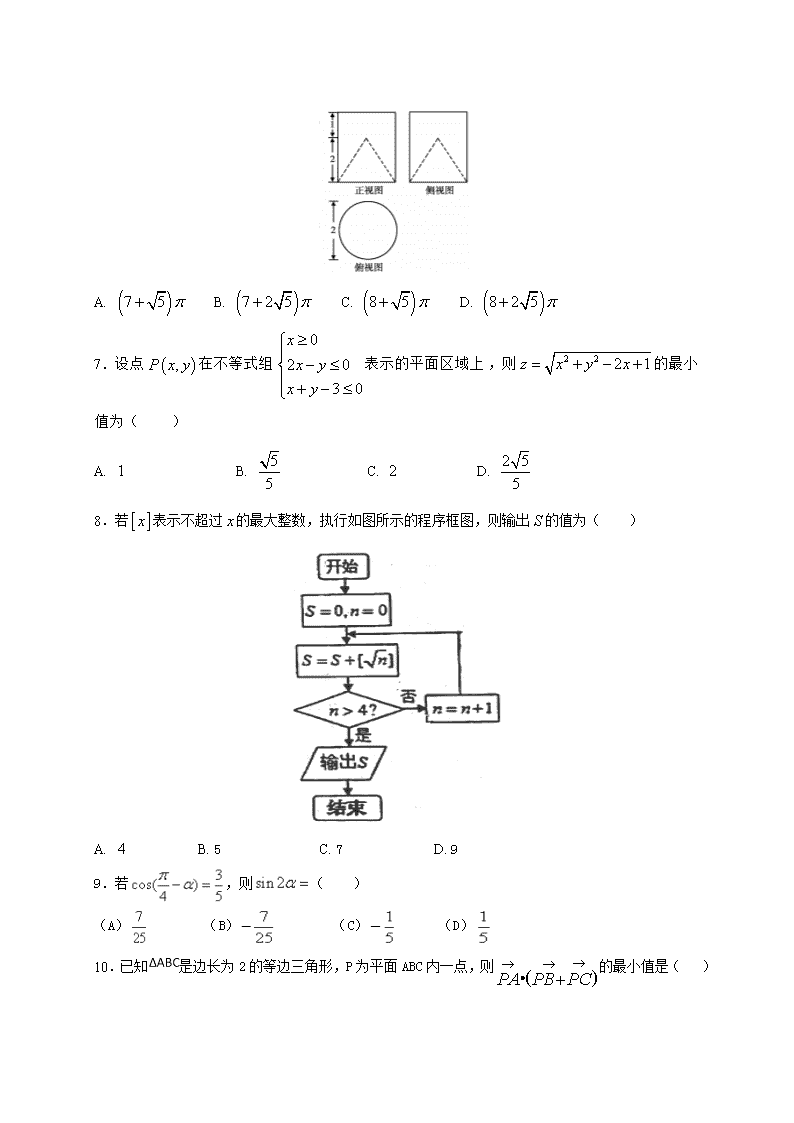
‎2017-2018学年第一学期2015级高三第二次月考 数学试题（理科）‎ 时间;120分钟 满分：150分 ‎ 第I卷（选择题）‎ 一、选择题（每题5分，共60分）‎ ‎1．设集合， ，则（ ）‎ A. B. C. D. ‎ ‎2．已知， 为虚数单位，若，则（ ）‎ A. B. C. D. ‎ ‎3．已知函数是定义在上的偶函数，且当时， ，则函数的大致图象为（ ）‎ A. B. C. D. ‎ ‎4．若将函数的图像向左平移个单位长度，则平移后图像的一个对称中心可以为（ ）‎ A. B. C. D. ‎ ‎5．在区间上随机地取两个数、,则事件“”发生的概率为（ ）‎ ‎（A） （B） （C） （D）‎ ‎6．在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示，则工艺部件的表面积为（ ）‎ A. B. C. D. ‎ ‎7．设点在不等式组表示的平面区域上，则的最小值为（ ）‎ A. B. C. D. ‎ ‎8．若表示不超过的最大整数，执行如图所示的程序框图，则输出的值为（ ）‎ A. B. 5 C. 7 D. 9‎ ‎9．若，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎10．已知是边长为2的等边三角形，P为平面ABC内一点，则的最小值是（ ）‎ A. B. C. D. ‎ ‎11．如图，过抛物线的焦点的直线交抛物线于点，交其准线于点C，若，且，则为（ ）‎ A. B. C. D. ‎ ‎12．若存在两个正实数，使得等式成立，其中为自然对数的底数，则实数的取值范围是( )‎ A. B. C. D. ‎ 第II卷（非选择题）‎ 二、填空题（每题5分，共20分）‎ ‎13．在的展开式中， 项的系数为______________‎ ‎14．函数是R上的偶函数，且在上是增函数，若，则实数的取值范围是_______________‎ ‎15．已知椭圆， 是的长轴的两个端点，点是上的一点，满足，设椭圆的离心率为，则______.‎ ‎16．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设三个内角， ， 所对的边分别为， ， ，面积为，则“三斜求积”公式为.若， ‎ ‎，则用“三斜求积”公式求得的面积为__________．‎ 三、解答题（共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17．（12分）已知等差数列的前项和为， ．  （1）求数列的通项公式；（2）设， 求数列的前项和．‎ ‎18．（12分）私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：‎ ‎（Ⅰ）完成被调查人员的频率分布直方图；‎ ‎（Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取2人进行追踪调查，求恰有2人不赞成的概率；‎ ‎（Ⅲ）在（Ⅱ）的条件下，再记选中的4人中不赞成“车辆限行”的人数为，求随机变量的分布列和数学期望．‎ ‎19．（12分）如图，边长为3的正方形所在平面与等腰直角三角形所在平面互相垂直， ，且， .‎ ‎（Ⅰ）求证： 平面；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎20．（12分）已知椭圆的离心率为，短轴长为．‎ ‎（Ⅰ）求椭圆的标准方程；‎ ‎（Ⅱ）若圆的切线与曲线相交于、两点，线段的中点为，求的最大值．‎ ‎21．（12分）已知函数.‎ ‎（1）若，求曲线在点处的切线；‎ ‎（2）若函数在其定义域内为增函数，求正实数的取值范围；‎ ‎（3）设函数，若在上至少存在一点，使得成立，求实数的取值范围.‎ 请考生在(22)、(23)两个题中任选一题作答.注意：只能做所选定的题目.如果多做，则按所做第一个题目计分，做答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑.‎ ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 已知直线的参数方程为（为参数），以原点为极点， 轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎(Ⅰ)求直线的普通方程及曲线的直角坐标方程；‎ ‎(Ⅱ)设直线与曲线交于两点，求.‎ ‎23．（本小题满分10分）选修4—5；不等式选讲 已知函数 ‎（Ⅰ）当时，解关于的不等式；‎ ‎（Ⅱ）若的解集包含，求实数的取值范围.‎ ‎2015级高三上学期第一次月考数学试题（理科）参考答案 ‎1--5．BDCAD 6--10．ADCBB 11—12 CD ‎11．【解析】设在准线上的射影分别为，则由于，则直线的斜率为， ，故，从而，故，即，故选C.‎ ‎12．【解析】由3x+a(2y−4ex)(lny−lnx)=0得3x+2a(y−2ex)ln=0，‎ 即，即设，则t>0，则条件等价为3+2a(t−2e)lnt=0，‎ 即(t−2e)lnt=−有解，设g(t)=(t−2e)lnt，为增函数，‎ ‎∵，∴当t>e时,g′(t)>0，当0

查看更多