- 2021-06-30 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2019届黑龙江佳木斯市富锦第一中学高二上学期第一次月考(2017-10)
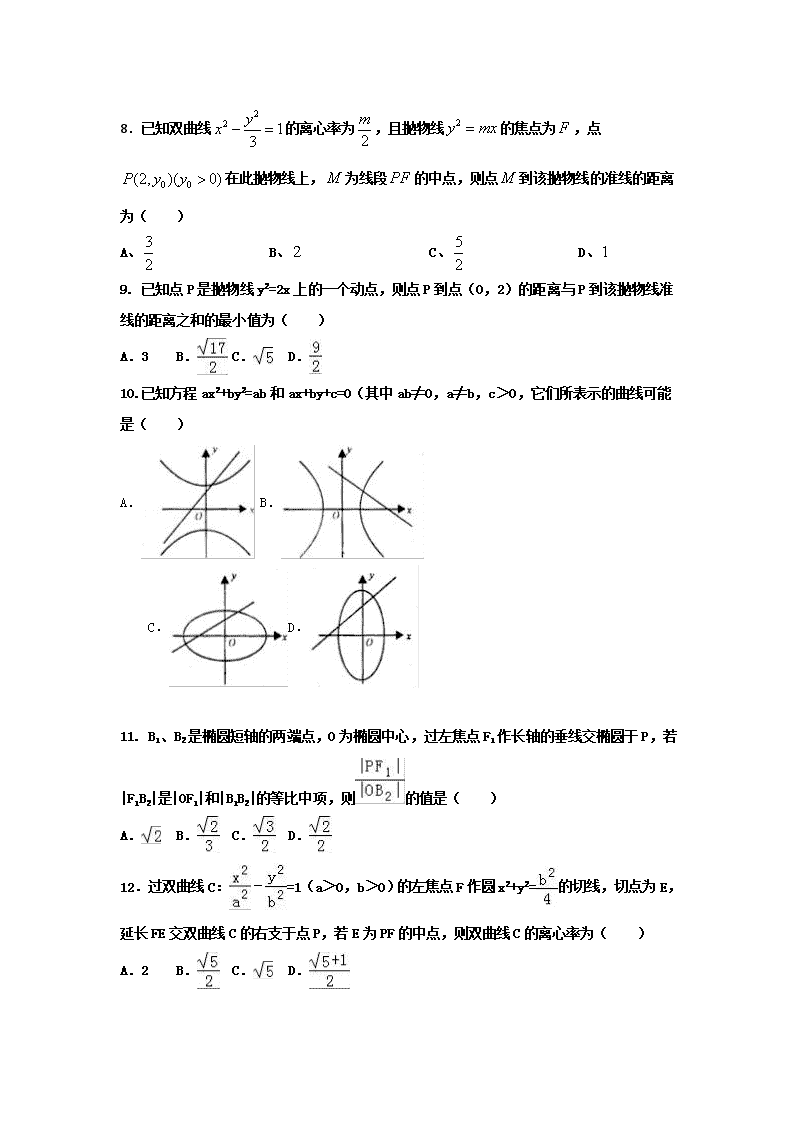
富锦一中2017-2018学年度第一学期高二第一次月考 数学试卷 理科 第Ⅰ卷(选择题,共60分) 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的. 1.若椭圆上的一点P到椭圆一个焦点的距离为3,则P到另一焦点的距离为( ) A.2 B.5 C.3 D. 7 2. 椭圆C: +=1(a>0)的长轴长为4,则C的离心率为( ) A. B. C. D. 3.双曲线x2﹣y2=﹣2的离心率为( )A. B. C.2 D. 4.双曲线﹣=1的焦点到其渐近线的距离为( ) A.2 B. C.3 D.4 5. 已知M(x0,y0)是双曲线C:-y2=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是( ) A.(,) B.(,) C.(,) D.(,) 6.已知圆C1:x2+y2﹣2x=0,圆C2:x2+y2﹣4y﹣1=0,两圆的相交弦为AB,则圆心C1 到AB的距离为( ) A. B. C. D. 7.若椭圆+=1的弦被点(4,2)平分,则此弦所在直线的斜率为( ) A.﹣2 B. C.2 D. 8.已知双曲线的离心率为,且抛物线的焦点为,点在此抛物线上,为线段的中点,则点到该抛物线的准线的距离为( ) A、 B、 C、 D、 9. 已知点P是抛物线y2=2x上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ) A.3 B. C. D. 10.已知方程ax2+by2=ab和ax+by+c=0(其中ab≠0,a≠b,c>0,它们所表示的曲线可能是( ) A. B. C.D. 11. B1、B2是椭圆短轴的两端点,O为椭圆中心,过左焦点F1作长轴的垂线交椭圆于P,若|F1B2|是|OF1|和|B1B2|的等比中项,则的值是( ) A. B. C. D. 12.过双曲线C:﹣=1(a>0,b>0)的左焦点F作圆x2+y2=的切线,切点为E,延长FE交双曲线C的右支于点P,若E为PF的中点,则双曲线C的离心率为( ) A.2 B. C. D. 二、 填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题纸上.) 13.△ABC的两个顶点为A(﹣1,0),B(1,0),△ABC周长为6,则C点轨迹为 . 14.抛物线y=4x2的焦点坐标是 . 15.若F1、F2是双曲线﹣y2=1的两个焦点,点P(8,y0)在双曲线上,则△F1PF2的面积为 . 16. 过双曲线的右顶点A作斜率为的直线,该直线与双曲线的两条渐近线的交点分别为B, C.若,则双曲线的离心率是 。 三、解答题(本大题共6小题,其中17题10分,其他每题各12分,共70分) 17.(10分)已知圆C:(x﹣1)2+(y﹣2)2=4. (1)求直线2x﹣y+4=0被圆C所截得的弦长; (2)求过点M(3,1)的圆C的切线方程. 18.(12分)已知线段AB的端点B坐标是(3,4),端点A在圆(x+1)2+y2=4上运动,求线段AB中点M的轨迹方程. 19.(12分)已知点A的坐标为(4,1),点B(﹣7,﹣2)关于直线y=x的对称点为C. (Ⅰ)求以A、C为直径的圆E的方程; (Ⅱ)设经过点A的直线l与圆E的另一个交点为D,|AD|=8,求直线l的方程 20.( 12分)已知椭圆C: +=1(a>b>0)的一个长轴顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N, (Ⅰ)求椭圆C的方程; (Ⅱ)当△AMN的面积为时,求k的值 21.( 12分)设F1、F2分别是椭圆的左、右焦点。 (1)若P是该椭圆上的一个动点,求的最大值和最小值; (2)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角 (其中O为坐标原点),求直线l的斜率k的取值范围。 22.( 12分)过双曲线的右支上的一点P作一直线l与两渐近线交于A、B两点,其中P是AB的中点; (1)求双曲线的渐近线方程; (2)当P坐标为(x0,2)时,求直线l的方程; (3)求证:|OA|•|OB|是一个定值. 答案及解析 1.D 2.C 3.B 4.B 5.C 6.A 7.D 8.C 9.B 10.A 11.D 12.C 13. 14. 15.5 16. 17解:圆C:(x﹣1)2+(y﹣2)2=4的圆心为(1,2),半径长r=2, (1)圆心C(1,2)到直线2x﹣y+4=0的距离为:, 所以直线2x﹣y+4=0被圆C所截得的弦长为: (2)因为(3﹣1)2+(1﹣2)2=5>4,所以点M在圆外, 当切线斜率存在时,设切线方称为:y﹣1=k(x﹣3) 即kx﹣y﹣3k+1=0, 圆心C(1,2)到直线kx﹣y﹣3k+1=0的距离为: 由题意有:,所以 此时切线方称为:,即3x﹣4y﹣5=0, 当切线斜率不存在时,直线x=3也与圆相切. 综上所述,所求切线方称为:3x﹣4y﹣5=0或x=3. 18.解答: 圆(x+1)2+y2=4的圆心为P(﹣1,0),半径长为2, 线段AB中点为M(x,y)取PB中点N,其坐标为N(1,2) ∵M、N为AB、PB的中点,∴MN∥PA且MN=PA=1. ∴动点M的轨迹为以N为圆心,半径长为1的圆. 所求轨迹方程为:(x﹣1)2+(y﹣2)2=1.也可用相关点法 19.(Ⅰ)点B(﹣7,﹣2)关于直线y=x的对称点为C(﹣2,﹣7), ∵AC为直径,AC中点E的坐标为(1,﹣3), ∴圆E的半径为|AE|=5, ∴圆E的方程为(x﹣1)2+(y+3)2=25.… (Ⅱ)当直线l的斜率不存在时,易求|AD|=8,此时直线l的方程为x=4,…(7分) 当直线l的斜率存在时,设l:y﹣1=k(x﹣4), ∴圆心E到直线l的距离d=,∵圆E的半径为5,|AD|=8,所以d=3, ∴=3,解得k=,∴直线l的方程为7x﹣24y﹣4=0. 综上所述,直线l的方程为x=4或7x﹣24y﹣4=0.…(12分) 20.解:(Ⅰ)∵椭圆一个顶点为A (2,0),离心率为, ∴∴b=∴椭圆C的方程为; (Ⅱ)直线y=k(x﹣1)与椭圆C联立,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0 设M(x1,y1),N(x2,y2),则x1+x2=, ∴|MN|== ∵A(2,0)到直线y=k(x﹣1)的距离为 ∴△AMN的面积S=∵△AMN的面积为, ∴∴k=±1. 21.(1)易知,, 所以,,设P,则 因为,故当,即点P为椭圆短轴端点时,有最小值-2; 当,即点P为椭圆长轴端点时,有最大值1。 (2)显然直线不满足题设条件。 可设直线:,A(),B() 联立,消去,整理得: ∴, 由得:或 ① 又 ∴ 又 ∵,即,∴ ② 故由①②得或。 22(1)双曲线的a=1,b=2,可得双曲线的渐近线方程为y=±x, 即为y=±2x; (2)令y=2可得x02=1+=2,解得x0=,(负的舍去), 设A(m,2m),B(n,﹣2n), 由P为AB的中点,可得m+n=2,2m﹣2n=4,解得m=+1,n=﹣1, 即有A(+1,2+2), 可得PA的斜率为k==2, 则直线l的方程为y﹣2=2(x﹣),即为y=2x﹣2; (3)证明:设P(x0,y0),即有x02﹣=1, 设A(m,2m),B(n,﹣2n), 由P为AB的中点,可得m+n=2x0,2m﹣2n=2y0, 解得m=x0+y0,n=x0﹣y0, 则|OA|•|OB|=|m|•|n|=5|mn|=5|(x0+y0)(x0﹣y0)| =5|x02﹣|=5为定值. 查看更多