数学（理）卷·2018届湖北省黄石市三中高二下学期期中考试（2017-04）

数学（理）卷·2018届湖北省黄石市三中高二下学期期中考试（2017-04）

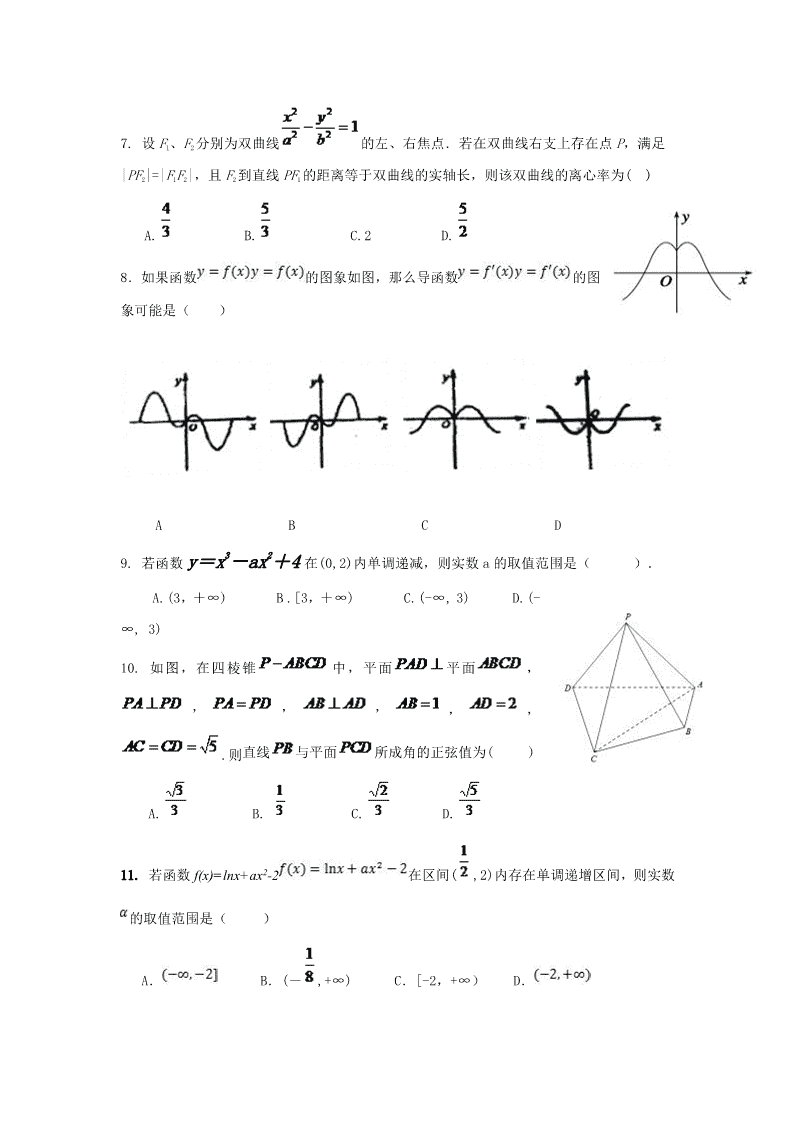
黄石三中 2016-2017 学年下学期期中考试 高二年级理科数学试卷 1．随机变量 服从二项分布 ～ ，且 则 等于（ ） A. B. C. 1 D. 0 2.若随机变量 ，则有下列结论： ，高三（1）班有 40 名同学，一次数学考试的成绩服从正态分布，平均分为 120 分，方差 100，理论上说在 130 分以上的人数为（ ） A. 19 B. 12 C. 6 D. 5 3. 广告投入对商品的销售额有较大影响．某电商对连续 5 个年度的广告费和销售额进行 统计，得到统计数据如下表（单位：万元）： 广告费 2 3 4 5 6 销售额 29 41 50 59 71 由上表可得回归方程为 ，据此模型，预测广告费为 万元时的销售额约为（ ） A． B． C． D． 4. 有六人排成一排，其中甲只能在排头或排尾，乙丙两人必须相邻，则满足要求的排法有 （ ） A．34 种 B．48 种 C．96 种 D．144 种 5. 由曲线 y＝x2，y＝x3 围成的封闭图形的面积为 ( ) A. 7 12 B． 1 4 C． 1 3 D． 1 12 6. 如图，某几何体的三视图中，正视图和侧视图都是半径为 的半圆 和相同的正三角形，其中三角形的上顶点是半圆的中点，底边在直径上， 则它的表面积是（ ） A. B. C. D. 7. 设 F1、F2 分别为双曲线 的左、右焦点．若在双曲线右支上存在点 P，满足 |PF2|=|F1F2|，且 F2 到直线 PF1 的距离等于双曲线的实轴长，则该双曲线的离心率为( ) A. B. C.2 D. 8．如果函数 的图象如图，那么导函数 的图 象可能是（ ） A B C D 9. 若函数 y＝x3－ax2＋4 在(0,2)内单调递减，则实数 a 的取值范围是（ ）． A.(3，＋∞) B .[3，＋∞) C.(-∞, 3) D.(- ∞, 3) 10. 如图，在四棱锥 中，平面 平面 ， ， ， ， ， ， .则直线 与平面 所成角的正弦值为( ) A. B. C. D. 11. 若函数 f(x)=lnx+ax2-2 在区间( ,2)内存在单调递增区间，则实数 的取值范围是（ ） A． B．(－ ,+∞) C．[-2，+∞） D． 12.设函数 在 上存在导数 ，对任意的 R，有 ，且 时， ．若 ，则实数 的取值范围为( ) A.[1, +∞) B.(-∞,2] C. (-∞,1] D.[2, +∞) 第Ⅱ卷 二、填空题：本题共 4 小题，每小题 5 分。 13．已知 为偶函数，当 时， ，则曲线 在点 处的切线方程是_______________. 14．在 的二项式中，所有项的二项式系数之和为 256，则常数项等于_________． 15.若 f(x)＝ x3＋sinx，－1≤x≤1， 2，1＜x≤2. 则 f(x)dx 等于_______． 16.已知 x=0 是函数 f(x)=(x-2a)(x2+a2x+2a3)的极小值点，则实数 a 的取值范围是_____． 三、解答题：解答应写出文字说明，证明过程或演算步骤。 17（本小题满分 10 分） 设 a 为实数，函数 f（x）=x3-x2-x+a， （Ⅰ）求 f（x）的极值； （Ⅱ）当 a 在什么范围内取值时，曲线 y=f（x）与 x 轴仅有一个交点。 18（本小题满分 12 分） 由 于 当 前 学 生 课 业负担较重，造成青少年视力普遍下降，现从某校随机抽取 16 名学生，经校医用对数视力 表检查得到每个学生的视力状况的茎叶图(以小数点前的一位 数字为茎，小数点后的一位数字为叶)如下： （Ⅰ）指出这组数据的众数和中位数； （Ⅱ）若视力测试结果不低于 5.0，则称为“好视力”，求校医从这 16 人中随机选取 3 人，至多有 1 人是“好视力”的概率； （Ⅲ）以这 16 人的样本数据来估计整个学校的总体数据，若从该校(人数很多)任选 3 人，记 表示抽到“好视力”学生的人数，求 的分布列及数学期望． 19（本小题满分 12 分） 如图，在四棱锥 中， 平面 ， 为直角， ， ， 分别为 的中点． （1）证明： 平面 ； （2）若 ，求二面角 的大小； （3）求点 到平面 的距离． 20．（本小题满分 12 分）如图，在平面直角坐标系 xOy 中，已知椭圆 x2 a2＋ y2 b2＝1(a＞b＞0) 的 焦距为 2，过右焦点 F 的直线 交椭圆于 两点，当 与 轴垂直时， 长为 ． （1）求椭圆的标准方程； （2）若椭圆上存在一点 P，使得 ，求 直线 的斜率. 21. (本小题满分 12 分）已知函数 ，其中 ． （I）若曲线 在点 处的切线 与直线 平行，求 的方程； （II）讨论函数 单调性． 22．（本小题满分 12 分）函数 ， ． （Ⅰ）讨论 的极值点的个数； （Ⅱ）若对于 ，总有 .（i）求实数 的范围；（ii）求证：对于 ， 不等式 成立． 高二理科数学参考答案 一、选择题：BCACD DBABA DC 二、填空题：13、2x+y+1=0 14、112 15、2 16、 或 17. 解：（Ⅰ）令 得： ，又∵当 x∈(-∞， )时， f′（x）＞0； 当 x∈( ，1)时，f′（x）＜0；当 x∈(1，+∞)时，f′（x）＞0， ∴ 与 分别为 f（x）的极大值与极小值点，∴f（x）极大值= ， f（x）极小值=a-1； （Ⅱ）∵f（x）在(-∞， )上单调递增， ∴当 x→-∞时，f（x）→-∞； 又 f（x）在(1，+∞)单调递增，当 x→+∞时，f（x）→+∞，∴当 f（x）极大值＜0 或 f（x） 极小值＞0 时，曲线 f（x）与 x 轴仅有一个交点，即 或 a-1＞0，∴a∈(-∞， ) ∪(1，+∞)。 18.解：（I）众数：4.6 和 4.7；中位数：4.75……………3 分 （II）设 表示所取 3 人中有个人是“好视力”，至多有 1 人是“好视力”记为事件， 则 …………………6 分 （III） 的可能取值为0，1，2，3 的分布列为 ………………12 分 19.解析：（1）证：由已知 DF∥AB 且 DAB 为直角，故 ABFD 是矩形，从而 AB BF． 又 PA 底面 ABCD, ∴平面 PAD 平面 ABCD， ∵AB AD，故 AB 平面 PAD,∴ AB PD， 在ΔPCD 内，E、F 分别是 PC、CD 的中点，EF//PD， ∴ AB EF．由此得 平面 ．.4 分 20 解：(1)由题意可知 ， 当 与 轴垂直时， ……2 分 因为 所以 ， 故椭圆的标准方程是： . ……4 分 (2)设直线 的斜率为 ，则直线 的方程： ，设点 , ， . 由 可得 ……6 分 则 ， . （）因 ，则 ，代入椭圆 方程有 ，又 ， ，化简得 ，即 ， ……10 分 将（）代入得 ， ，即 . 故直线 的斜率为 .… 12 分 21 解 当 时， ，∴ 的方程为： ． （II）令 得 ， 当 ，即 时， 在 上递增 当 即 时 ， 令 得 ， 递 增 ； 令 得 递减，综上所述，当 时， 的增区间为 ，减区 间为 ；当 时， 在 上递增． 22.解：（Ⅰ）解法一：由题意得 ， 令 （1）当 ，即 时， 对 恒成立 即 对 恒成立，此时 没有极值点；…………2 分 （2）当 ，即 ① 时，设方程 两个不同实根为 ，不妨设 则 ，故 ∴ 时 ； 在 时 故 是函数 的两个极值点. ② 时 ， 设 方 程 两 个 不 同 实 根 为 ， 则 ，故 ∴ 时， ；故函数 没有极值点. …………4 分 综上，当 时，函数 有两个极值点； 当 时，函数 没有极值 点. ……5 分 解法二： , …………1 分 ,①当 ，即 时， 对 恒成立， 在 单调增， 没有极值点； …………3 分 ②当 ，即 时，方程 有两个不等正数解 ， 不 妨 设 ， 则 当 时， 增； 时， 减； 时， 增，所以 分别为 极大值点和极小值点， 有两个极值点. 综上所述，当 时， 没有极值点；当 时， 有两个极值 点.………5 分 （Ⅱ）（i） ，由 ，即 对于 恒 成 立 ， 设 ， ， ， 时， 减， 时， 增， ， ． …………………………………… 9 分 （ii）由（i）知，当 时有 ，即： ， ……①当且仅当 时取等号, …………………………… 10 分 以下证明： ，设 ， ， 当 时 减， 时 增， ， ，……②当且仅当 时取等号； 由于①②等号不同时成立，故有 .……………………………12 分